お気楽 NumPy プログラミング超入門

●複素数

今回は Python (NumPy) の複素数について簡単にまとめてみました。

複素数 \(a + bi\) (a : 実部, b : 虚部, i : 虚数単位) は a + bj と表す

j のかわりに大文字の J を使ってもよい
虚部 b を省略することはできない
1 + j はエラーになるので 1 + 1j と書くこと

実部と虚部は浮動小数点数 (float)
複素数のデータ型名は complex

NumPy でのデフォルトのデータ型は complex128
NumPy にはデータ型を判定する述語 isreal(), iscomplex(), iscomplexobj() がある

コンストラクタ complex は複素数を生成する

complex(a, b)

a が実部で、b が虚部

複素数の配列は NumPy のコンストラクタ array() で簡単に生成できる
実部は real で、虚部は imag で取得する

NumPy では関数 real() と imag() でも取得できる

四則演算 (+, -, *, /) や累乗 (**) はそのまま使える
比較演算子は = と != が使用できる

複素数の場合、大小関係 (<, >, <=, >=) は使えない

複素数を極形式 \(z = r(\cos \theta + i \sin \theta)\) で表した場合、r を絶対値、\(\theta\) を偏角という
絶対値は関数 abs で、偏角はモジュール cmath の関数 phase で求める

cmath には複素数を扱う関数が定義されている
NumPy では関数 angle を使ってもよい

複素数 z の絶対値と偏角は cmath.polar(z) で求めることもできる
返り値はタプル (絶対値, 偏角)
cmath.rect() は極形式 (絶対値, 偏角) と等しい複素数を生成する
複素共役はメソッド conjugate() で求める

NumPy では関数 conjugate() または conj() を使うと便利

cmath や NumPy の数学関数 (sqrt, exp, log, 三角関数など) は複素数も使用できる

>>> import numpy as np
>>> import cmath
>>> a = complex(1, 2)
>>> a
(1+2j)
>>> b = 3 + 4j
>>> b
(3+4j)
>>> c = np.array([a, b])
>>> c
array([ 1.+2.j,  3.+4.j])
>>> type(a)
<class 'complex'>
>>> np.iscomplex(a)
True
>>> np.iscomplex(c)
array([ True,  True], dtype=bool)
>>> np.iscomplex(1.234)
False
>>> np.isreal(a)
False
>>> np.isreal(c)
array([False, False], dtype=bool)
>>> np.isreal(1.2345)
True

>>> a + b
(4+6j)
>>> a - b
(-2-2j)
>>> a * b
(-5+10j)
>>> a / b
(0.44+0.08j)
>>> a ** 2
(-3+4j)
>>> a ** 3
(-11-2j)
>>> a == a
True
>>> a != a
False
>>> a != b
True

>>> a.real
1.0
>>> a.imag
2.0
>>> np.real(a)
1.0
>>> np.real(c)
array([ 1.,  3.])
>>> np.imag(a)
2.0
>>> np.imag(c)
array([ 2.,  4.])

>>> abs(a)
2.23606797749979
>>> abs(b)
5.0
>>> np.abs(c)
array([ 2.23606798,  5.        ])
>>> cmath.phase(a)
1.1071487177940904
>>> np.angle(a)
1.1071487177940904
>>> cmath.phase(b)
0.9272952180016122
>>> np.angle(b)
0.92729521800161219
>>> np.angle(c)
array([ 1.10714872,  0.92729522])

>>> cmath.polar(a)
(2.23606797749979, 1.1071487177940904)
>>> cmath.polar(b)
(5.0, 0.9272952180016122)
>>> cmath.rect(2.23606797749979, 1.1071487177940904)
(1.0000000000000002+2j)
>>> cmath.rect(5.0, 0.9272952180016122)
(3.0000000000000004+3.9999999999999996j)

>>> a.conjugate()
(1-2j)
>>> b.conjugate()
(3-4j)
>>> np.conj(a)
(1-2j)
>>> np.conj(b)
(3-4j)
>>> np.conj(c)
array([ 1.-2.j,  3.-4.j])

>>> cmath.sqrt(-1)
1j
>>> cmath.sqrt(-2)
1.4142135623730951j
>>> np.sqrt(-1+0j)
1j
>>> np.sqrt(-2+0j)
1.4142135623730951j
>>> np.sqrt(c)
array([ 1.27201965+0.78615138j,  2.00000000+1.j        ])
>>> cmath.exp(complex(0,cmath.pi/4))
(0.7071067811865476+0.7071067811865475j)
>>> cmath.exp(complex(0,cmath.pi)) + 1
1.2246467991473532e-16j
>>> np.exp(a)
(-1.1312043837568135+2.4717266720048188j)
>>> np.exp(b)
(-13.128783081462158-15.200784463067954j)
>>> np.exp(c)
array([ -1.13120438 +2.47172667j, -13.12878308-15.20078446j])

●複素ベクトル

成分 (要素) が複素数のベクトルを「複素ベクトル」という
複素共役を * で表すと、ベクトル \(v = (v_1, v_2, \ldots, v_n)\) の複素共役は \(v^* = ({v_1}^*, {v_2}^*, \ldots, {v_n}^*)\) となる
複素ベクトル \(u, v\) の内積 \((u, v)\) を \(\displaystyle \sum_{i=1}^n u_i {v_i}^*\) と定義する

これをエルミート内積という
\((u, v) = \displaystyle \sum_{i=1}^n {u_i}^* \,v_i\) と定義してもよい
エルミート内積は関数 numpy.vdot(u, v) で求めることができる
NumPy では \((u, v) = \displaystyle \sum_{i=1}^n {u_i}^* \,v_i\) で計算している
演算子 u @ v, メソッド v.dot(u), 関数 numpy.dot(u, v) は複素共役をとらずに \(\sum u_i v_i\) を計算する

エルミート内積の性質

\((u, v) = (v, u)^*\)
\((u + v, w) = (u, w) + (v, w), (u, v + w) = (u, v) + (u, w)\)
\(a(u, v) = (au, v) = (u, a^* v)\), a : 定数 (複素数)
\((u, u) \geq 0, (u, u) = 0\) のとき \(u\) は零ベクトル

複素ベクトル \(v\) のノルムは内積を使って \(\sqrt {(v, v)}\) と定義される

複素ベクトルのノルムは実数になる
v のノルムは関数 numpy.linalg.norm(v) で求めることができる

>>> import numpy as np
>>> a = np.array([1+2j,3+4j])
>>> a
array([ 1.+2.j,  3.+4.j])
>>> b = np.array([5+6j, 7+8j])
>>> b
array([ 5.+6.j,  7.+8.j])
>>> np.conjugate(a)
array([ 1.-2.j,  3.-4.j])
>>> np.conj(b)
array([ 5.-6.j,  7.-8.j])

>>> a + b
array([  6. +8.j,  10.+12.j])
>>> a - b
array([-4.-4.j, -4.-4.j])
>>> a * b
array([ -7.+16.j, -11.+52.j])
>>> a / b
array([ 0.27868852+0.06557377j,  0.46902655+0.03539823j])

>>> c = 1 - 1j
>>> a + c
array([ 2.+1.j,  4.+3.j])
>>> a - c
array([ 0.+3.j,  2.+5.j])
>>> a * c
array([ 3.+1.j,  7.+1.j])
>>> a / c
array([-0.5+1.5j, -0.5+3.5j])

>>> np.vdot(a, b)
(70-8j)
>>> np.vdot(b, a)
(70+8j)
>>> np.conj(a) @ b
(70-8j)
>>> a @ np.conj(b)
(70+8j)
>>> a @ b
(-18+68j)

>>> np.vdot(a, a)
(30+0j)
>>> np.vdot(b, b)
(174+0j)
>>> np.linalg.norm(a)
5.4772255750516612
>>> np.linalg.norm(b)
13.19090595827292

●複素行列

成分が複素数の行列を「複素行列」という

成分がすべて実数の行列を「実行列」という

複素行列 \(A\) において、各成分をその複素共役に変えた行列を複素共役行列といい \(A^*\) で表す
\(A\) を転置して各成分を複素共役に変えた行列を「随伴行列 (adjoint matrix)」といい \(A^{\dagger}\) で表す

\(A\) の各成分を複素共役に変えてから転置してもよい
\(A^{\dagger} = (A^{\mathrm{T}})^* = (A^*)^{\mathrm{T}}\)
この操作をエルミート転置 (Hermitian transpose) という
NumPy でエルミート転置を行うには numpy.conj(A.T) とする

随伴行列の性質

\((A^{\dagger})^{\dagger} = A\)
\((A + B)^{\dagger} = A^{\dagger} + B^{\dagger}\)
\((a A)^{\dagger} = a^* A^{\dagger}\), a : 定数 (複素数)
\((A B)^{\dagger} = B^{\dagger} A^{\dagger}\)
\(\det A^{\dagger} = (\det A)^*, \ \mathrm{Tr} \ A^{\dagger} = (\mathrm{Tr} \ A)^*\), \(A\) は正方行列
(\(A^{-1})^{\dagger} = (A^{\dagger})^{-1}\), \(A\) は正則行列
\((A u, v) = (u, A^{\dagger} \, v)\), ( , ) はエルミート内積

\(A^{\dagger} = A\) を満たすとき、A を「エルミート行列 (Hermitian matrix)」という

エルミート行列の主対角成分は実数になる
実行列の場合、エルミート行列は対称行列になる

\(A^{\dagger} = -A\) を満たすとき、\(A\) を「歪エルミート行列 (skew Hermitian matrix)」という
\(A^{\dagger} = A^{-1}\) を満たすとき、A を「ユニタリ行列 (unitary matrix)」という

実行列の場合、ユニタリ行列は直交行列になる

>>> a = np.array([[1+1j, 1-1j], [2+3j, 2+1j]])
>>> a
array([[ 1.+1.j,  1.-1.j],
       [ 2.+3.j,  2.+1.j]])
>>> a.T
array([[ 1.+1.j,  2.+3.j],
       [ 1.-1.j,  2.+1.j]])

>>> def htr(a): return np.conj(a.T)
...
>>> htr(a)
array([[ 1.-1.j,  2.-3.j],
       [ 1.+1.j,  2.-1.j]])
>>> htr(htr(a))
array([[ 1.+1.j,  1.-1.j],
       [ 2.+3.j,  2.+1.j]])

>>> b = np.array([[1+0j, 1+1j],[1-1j, 0+1j]])
>>> b
array([[ 1.+0.j,  1.+1.j],
       [ 1.-1.j,  0.+1.j]])
>>> htr(a + b)
array([[ 2.-1.j,  3.-2.j],
       [ 2.-0.j,  2.-2.j]])
>>> htr(a) + htr(b)
array([[ 2.-1.j,  3.-2.j],
       [ 2.+0.j,  2.-2.j]])
>>> c
(1-1j)
>>> htr(c * a)
array([[ 2.-0.j,  5.-1.j],
       [ 0.+2.j,  3.+1.j]])
>>> np.conj(c) * htr(a)
array([[ 2.+0.j,  5.-1.j],
       [ 0.+2.j,  3.+1.j]])
>>> htr(a @ b)
array([[ 1.+1.j,  5.-2.j],
       [ 1.-3.j, -2.-7.j]])
>>> htr(b) @ htr(a)
array([[ 1.+1.j,  5.-2.j],
       [ 1.-3.j, -2.-7.j]])

>>> np.linalg.det(a)
(-4.0000000000000009+2.0000000000000009j)
>>> np.linalg.det(htr(a))
(-4-2j)
>>> np.conj(np.linalg.det(a))
(-4.0000000000000009-2.0000000000000009j)
>>> np.linalg.inv(a)
array([[-0.3-0.4j,  0.3-0.1j],
       [ 0.1+0.8j, -0.1-0.3j]])
>>> htr(np.linalg.inv(a))
array([[-0.3+0.4j,  0.1-0.8j],
       [ 0.3+0.1j, -0.1+0.3j]])
>>> np.linalg.inv(htr(a))
array([[-0.3+0.4j,  0.1-0.8j],
       [ 0.3+0.1j, -0.1+0.3j]])

>>> u = np.array([1+2j, 3+4j])
>>> u
array([ 1.+2.j,  3.+4.j])
>>> v = np.array([5+6j, 7+8j])
>>> v
array([ 5.+6.j,  7.+8.j])
>>> a @ u
array([ 6. +4.j, -2.+18.j])
>>> np.vdot(a @ u, v)
(184-126j)
>>> np.vdot(u, htr(a) @ v)
(184-126j)

●複素関数のグラフ

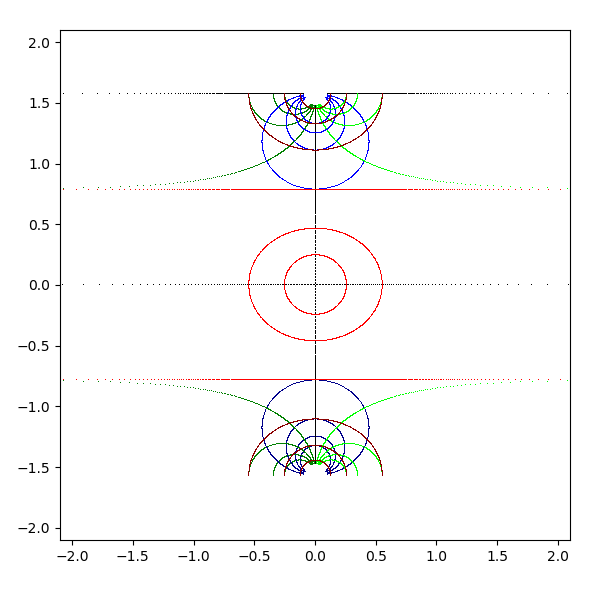
参考文献『COMMON LISP 第 2 版』と参考 URL『複素関数で遊ぼう』を参考にして、複素関数 w = f(z) の値域 (w) をグラフにしてみました。下図に示す複素平面を考えます。

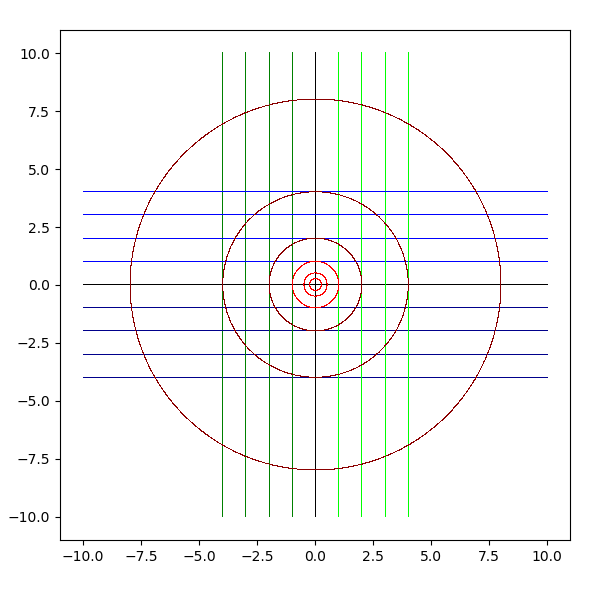
複素平面は横軸が実軸で、縦軸が虚軸となります。実軸と虚軸は黒 (black) で描画します。横線を青 (blue と darkblue) で、縦線を緑 (lime と green) で、原点を中心とした円を赤 (red と darkred) で描画しています。これを複素関数 sqrt, exp, log, sin, arcsin, cos, arccos, tan, arctan, sinh, arcsinh, cosh, arccosh, tanh, arctanh に渡して、評価結果を複素平面に描画します。

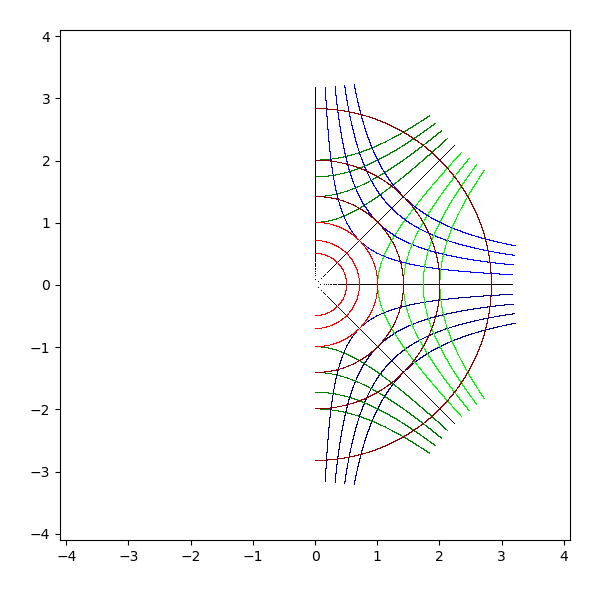
sqrt(z)

正の実軸は自身に、負の実軸は正の虚軸に写像される
正の虚軸は右上 45 度の半直線に、負の虚軸は右下 45 度の半直線に写像される
直線は原点を中心とする直角双曲線 (あるいはその一部) に写像される

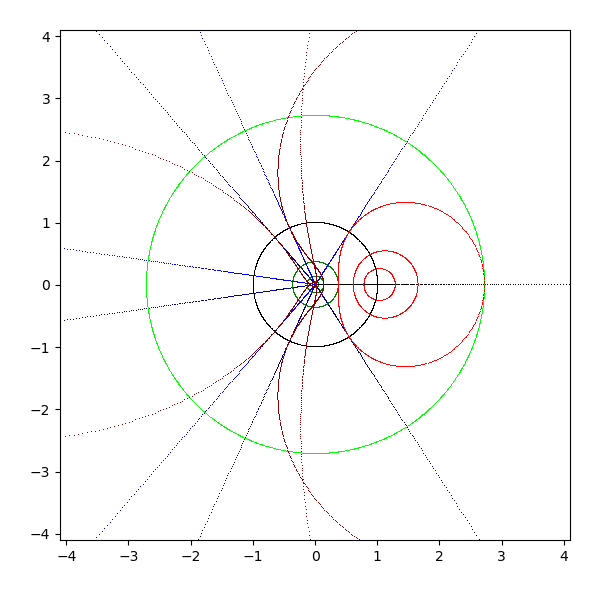
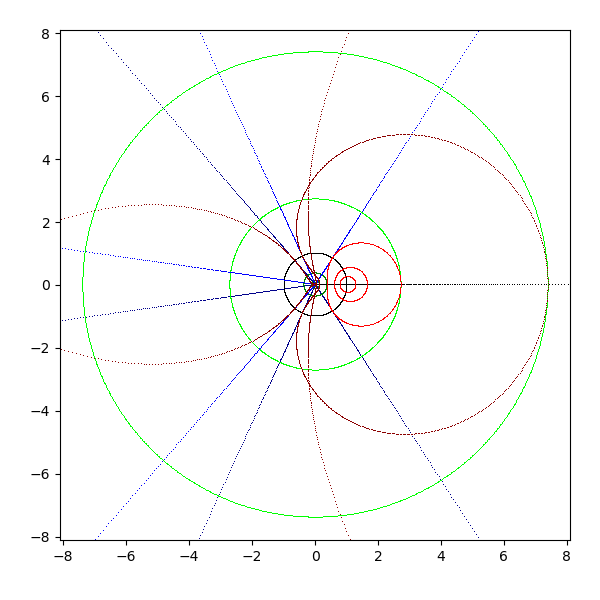
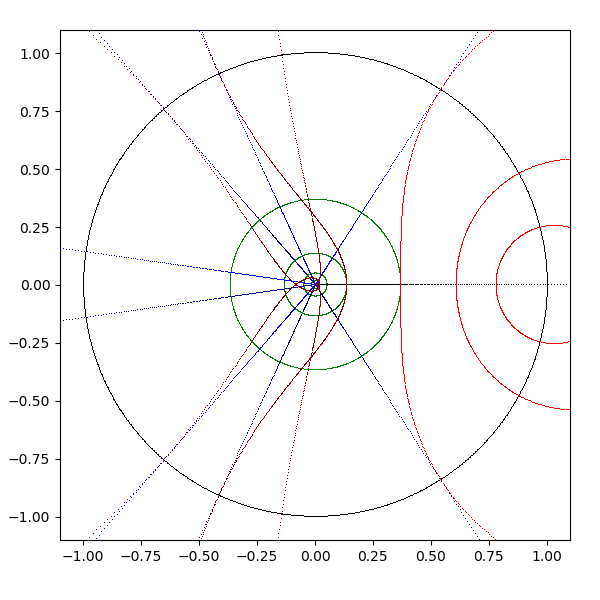
exp(z)

水平の直線は原点から伸びる半直線に、垂直の直線は原点を中心とする円に写像される
虚軸は単位円 (原点を中心に半径 1 の円) に写像される
原点は 1 (1+0i) に写像される
半径 1 以下の円は 1 (1+0i) を中心とする閉曲線に写像される

log(z)

原点を通る直線は水平な直線に、原点を中心とする円は垂直な直線に写像される
正の実軸は実軸に、負の実軸は高さ pi の水平線に写像される
正の虚軸は高さ pi/2 の水平線に、負の虚軸は高さ -pi/2 の錐変遷に写像される
半径 1 の円は虚軸に、1 より大きい円は右半面に、1 より小さい円は左半面に写像される

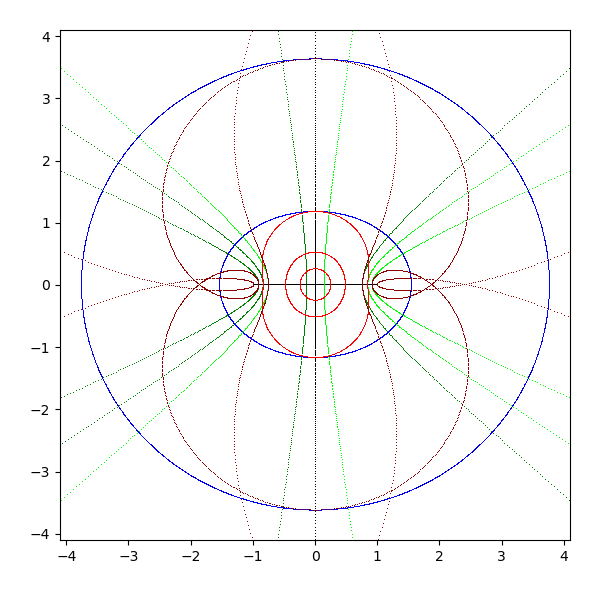
sin(z)

実軸は実軸上の [-1 + 0i, 1 + 0i] の区間に、虚軸は自分自身に写像される
水平な直線は楕円に写像される
垂直な直線は双曲線に写像される

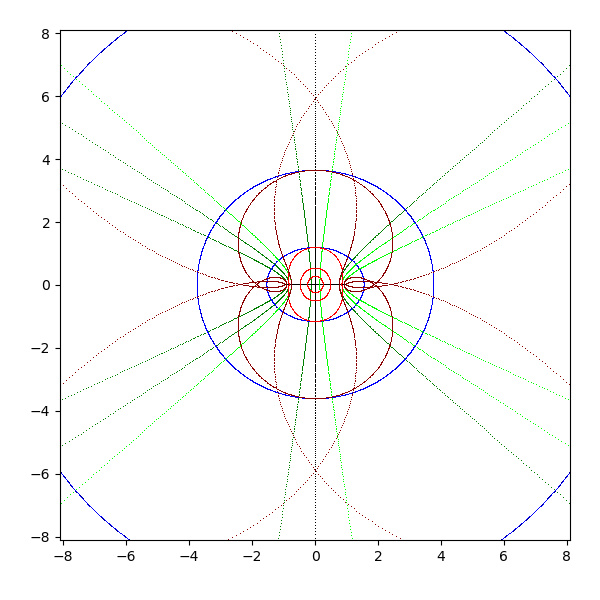
arcsin(z)

円は水平方向に引き伸ばすように写像される
虚軸は自分自身に、実軸は -pi/2 + ∞i, -pi/2 + 0i, pi/2 + 0i, pi/2 + ∞i の折れ線に写像される
ただし、正の実軸で負のゼロを選ぶと -pi/2 + ∞i, -pi/2 + 0i, pi/2 - 0i, pi/2 - ∞i に写像される

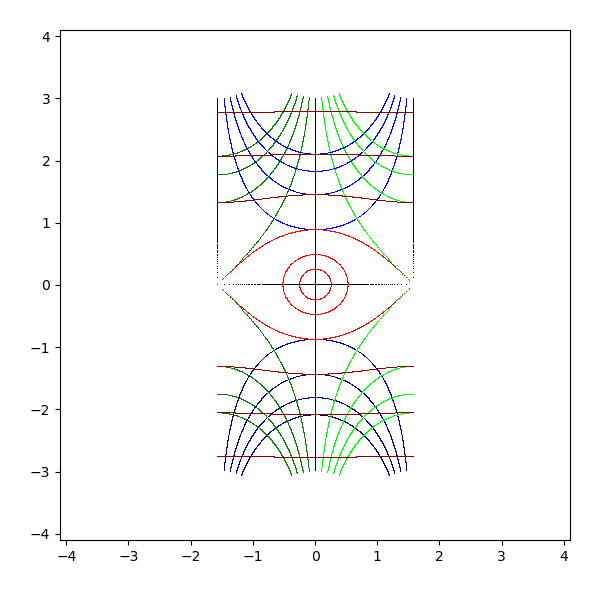
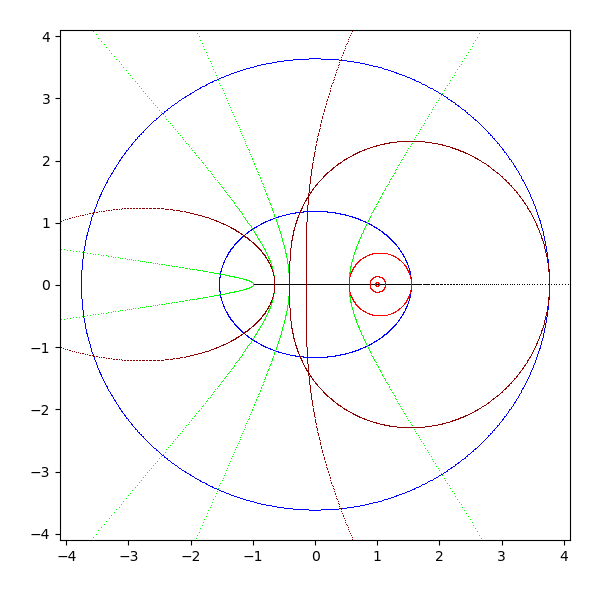
cos(z)

水平な直線は楕円に写像される
垂直な直線は双曲線に写像される
実軸は実軸上の [-1 + 0i, 1 + 0i] の区間に、虚軸は実軸の [1 + 0i, +∞+ 0i] に写像される
原点は実軸の 1 + 0i に写像される

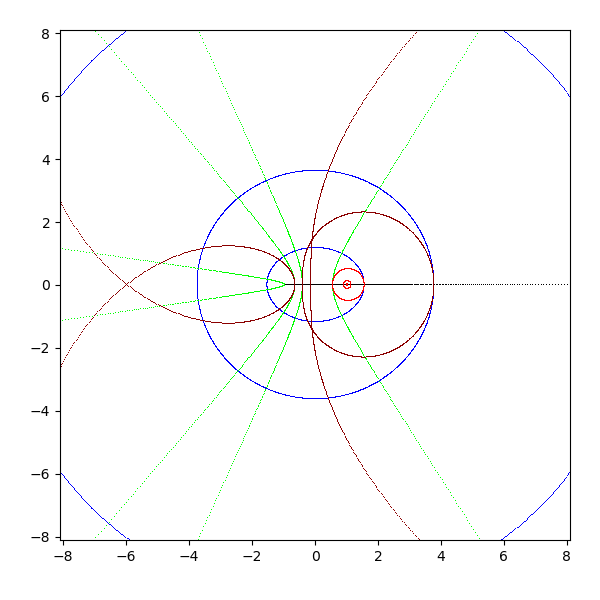
arccos(z)

公式 arccos z = pi/2 - arcsin z
arccos z は arcsin z を逆さまにして pi/2 右にずらしたものになる
虚軸は pi/2 のところに逆さまに、実軸は -pi/2 - ∞i, -pi/2 + 0i, pi/2 + 0i, pi/2 - ∞i の折れ線に写像される
ただし、負の実軸で負のゼロを選ぶと -pi/2 + ∞i, -pi/2 - 0i, pi/2 + 0i, pi/2 - ∞i に写像される

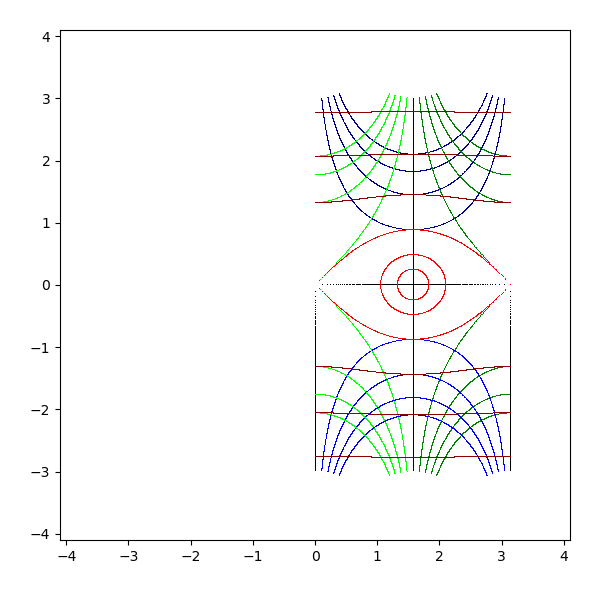
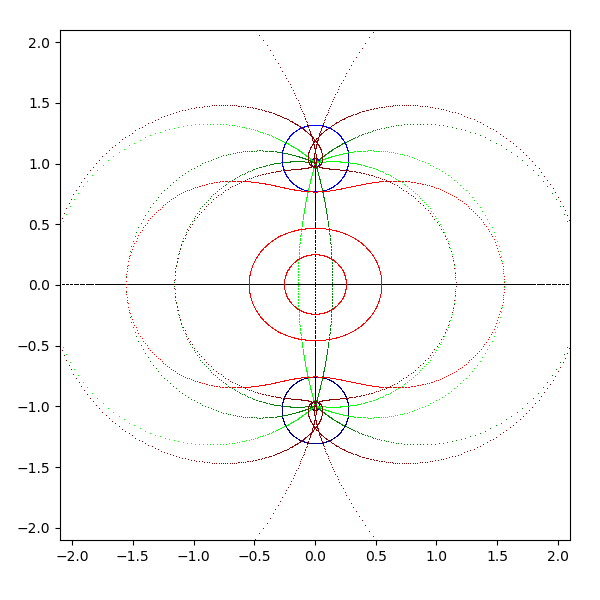
tan(z)

実軸は自分自身に、虚軸は [0 - i, 0 + i] に +∞i は -i に、-∞i は i に対応して写像される
水平な直線は 0 + i と 0 - i を囲む円に写像される
垂直な直線は 0 + i と 0 - i を通る円弧に写像される

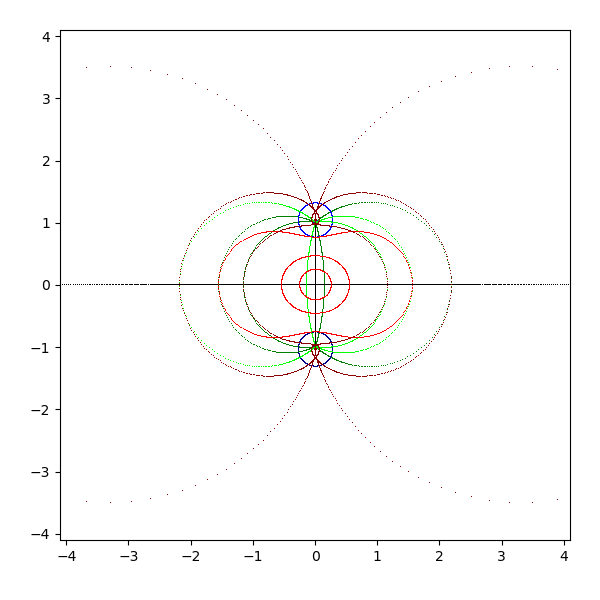
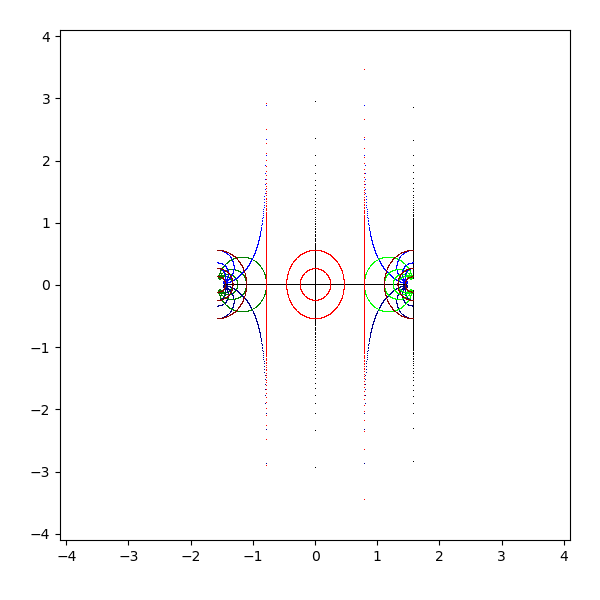
arctan(z)

実軸は [-pi/2 + 0i, pi/2 + 0i] に写像され、-∞ が -pi/2 に、∞が pi/2 に対応する
虚軸は [0 - ∞i, 0 - i] が [pi/2 - ∞i, pi/2 + 0i] に、[0 - i, 0 + i] が [0 - ∞i, 0 + ∞i] に、
[0 + i, 0 + ∞i] が [pi/2 + 0i, pi/2 + ∞i] に写像される
ただし、負の虚軸で負のゼロを用いると [-0.0 - ∞i, -0.0 - i] は [-pi/2 - ∞i, -pi/2 + 0i] に写像される

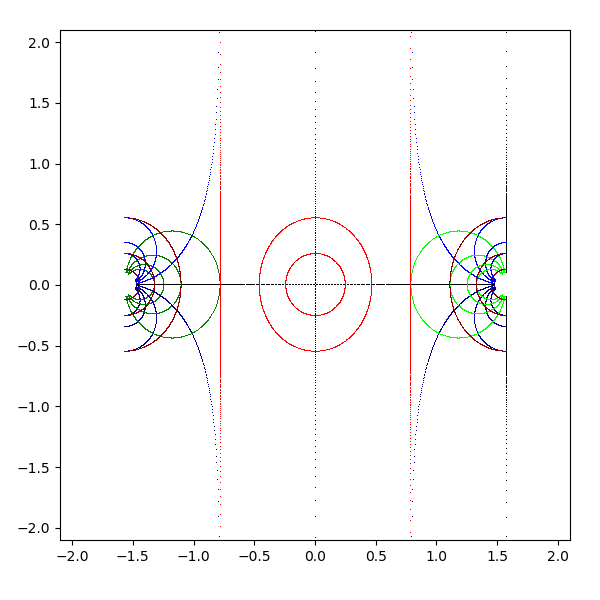
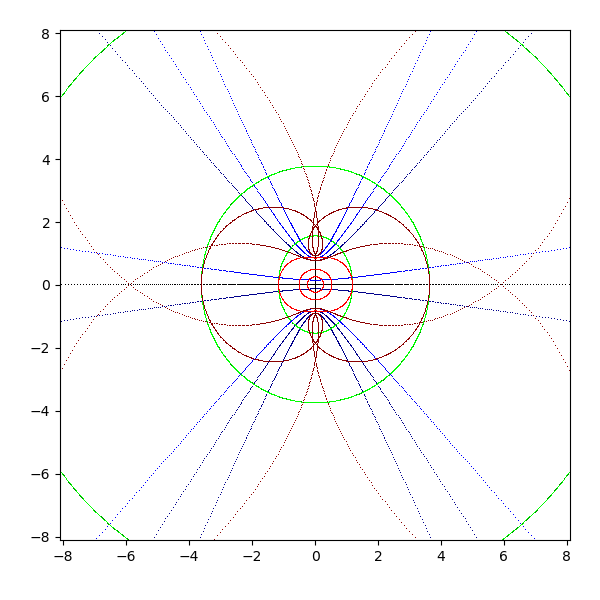
sinh(z)

sinh のグラフは sin のグラフを pi/2 回転したものではない
sinh では水平な直線が双曲線に、垂直な直線が円に写像されている
公式 sinh iz = i sin z (sinh z = -i sin iz)
z を pi/2 回転して sin に適用し、それを -pi/2 回転すると sinh z になる

z = a + bi に i を乗算すると -b + ai になる (pi/2 回転)
z = a + bi に -i を乗算すると b - ai になる (-pi/2 回転)

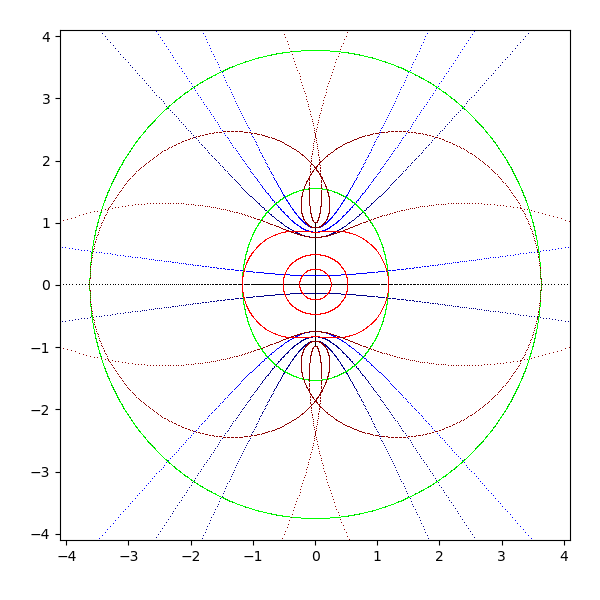
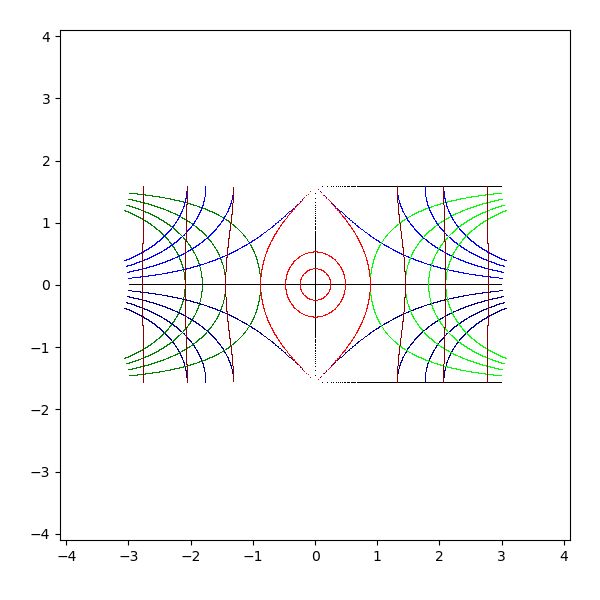
arcsinh(z)

公式 arcsin iz = i arcsinh z (arcsinh z = -i arcsin iz)
z を pi/2 回転して arcsin に適用し、それを -pi/2 回転すると arcsinh z になる

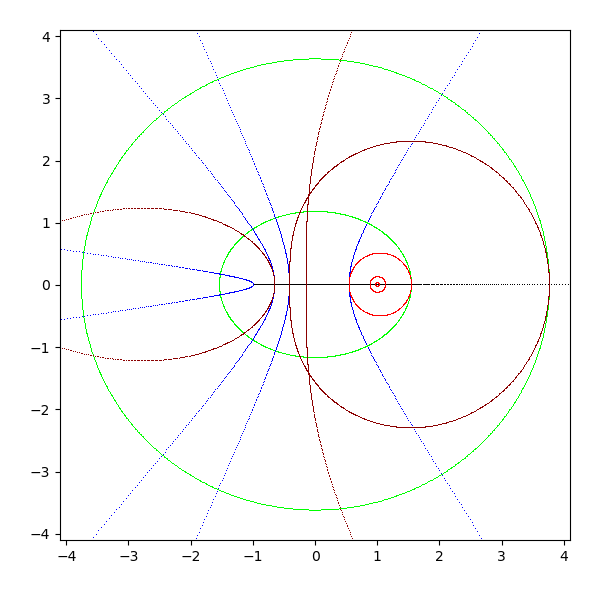
cosh(z)

公式 cosh iz = cos z (cosh z = cos -iz = cos iz)
z を pi/2 回転して cos に適用したものが cosh になる

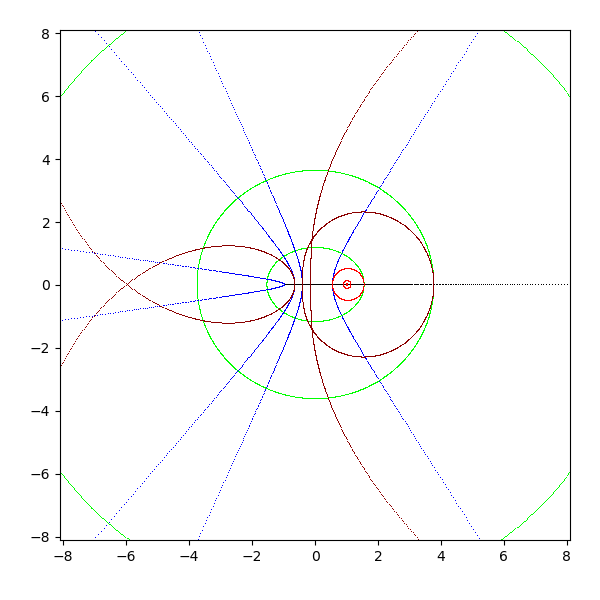
arccosh(z)

arccos z の第 4 象限を pi/2 回転し、第 1 象限を -pi/2 回転したようにみえる

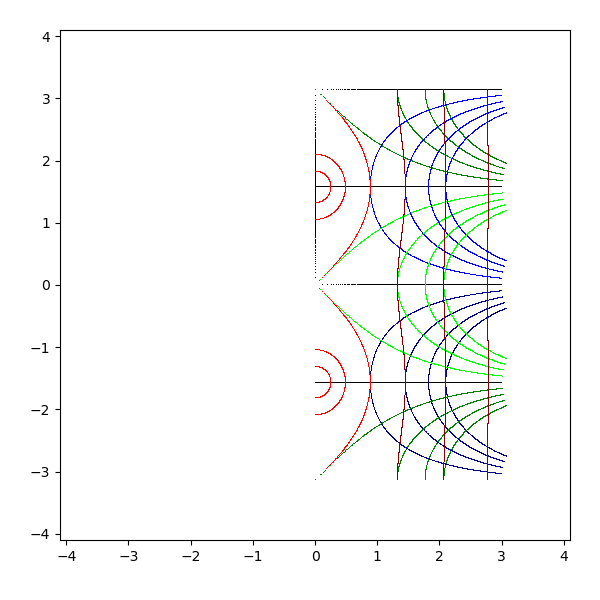
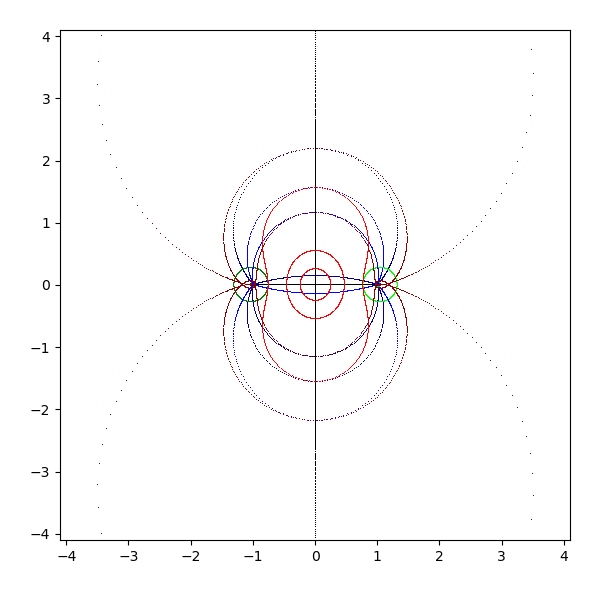
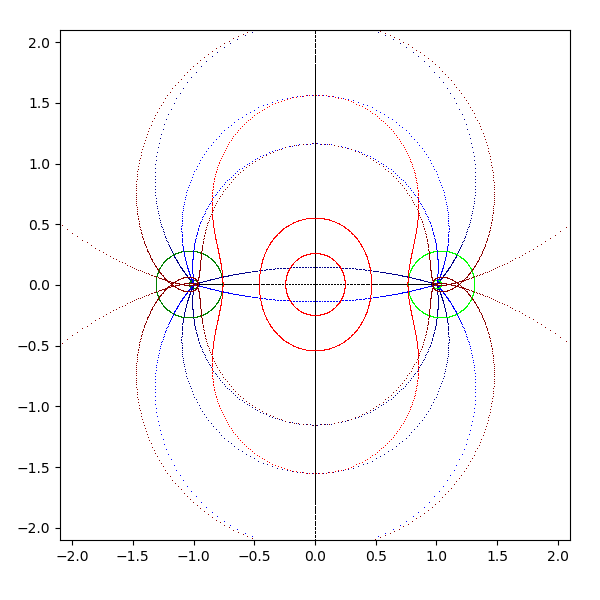
tanh(z)

公式 tan iz = i tanh z (tanh z = -i tan iz)
z を pi/2 回転して tan に適用し、それを -pi/2 回転すると tanh になる

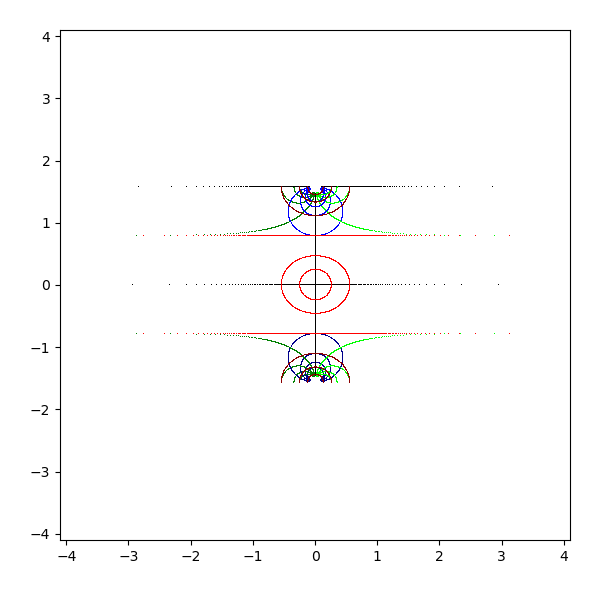
arctanh(z)

公式 arctan iz = i arctanh z (arctanh z = -i arctan iz)
z を pi/2 回転して arctan に適用し、それを -pi/2 回転すると arctanh になる

●プログラムリスト

リスト : 複素関数の描画

import math
import numpy as np
import matplotlib.pyplot as plt

plt.figure(figsize=(6, 6))
plt.subplots_adjust(left=0.1, right=0.95, bottom=0.1, top=0.95)
plt.xlim(-4.1, 4.1)
plt.ylim(-4.1, 4.1)

# 描画する複素関数をセットする
cfunc = np.sqrt

for i in np.linspace(-4.0, 4.0, 9):
    # 横線
    x = np.linspace(-10.0, 10.0, 1600)
    y = np.full(1600, i)
    z = np.array([complex(a, b) for a in x for b in y])
    w = cfunc(z)
    if i > 0.0:
        c = 'blue'
    elif i < 0.0:
        c = 'darkblue'
    else:
        c = 'black'
    plt.plot(np.real(w), np.imag(w), ',', color = c)
    # 縦線
    y = np.linspace(-10.0, 10.0, 1600)
    x = np.full(1600, i)
    z = np.array([complex(a, b) for a in x for b in y])
    w = cfunc(z)
    if i > 0.0:
        c = 'lime'
    elif i < 0.0:
        c = 'green'
    else:
        c = 'black'
    plt.plot(np.real(w), np.imag(w), ',', color= c)
# 円
for r, n in [(0.25, 800), (0.5, 800), (1.0, 800), (2.0, 1600), (4.0, 1600), (8.0, 3200)]:
    theta = np.linspace(-math.pi, math.pi, n)
    z = np.array([complex(r * math.cos(x), r * math.sin(x)) for x in theta])
    w = cfunc(z)
    if r > 1.0:
        c = 'darkred'
    else:
        c = 'red'
    plt.plot(np.real(w), np.imag(w), ',', color = c)

plt.gca().set_aspect('equal')
plt.show()

●参考文献, URL

Guy L. Steele Jr., 『COMMON LISP 第 2 版』, 共立出版, 1991
複素関数で遊ぼう, (雑記帳 | 人生やっていき)