●巡回セールスマン問題
都市が下図のように散らばっているとします。セールスマンは各都市を 1 回ずつもれなく訪問して帰ってこなくてはなりません。このとき、一番短い巡路 (全ての都市を含む単純な閉路) を見つけるのが「巡回セールスマン問題 (Traveling Salesperson Problem, TSP)」です。
巡路の長さは自由に定義してもかまいません。たとえば、時間であったり料金であってもいいのですが、今回はオーソドックスに「距離」と定義することにしましょう。
Ａ Ｂ
● ●
● ●
Ｅ Ｆ
● ●
Ｃ Ｄ
都市の配置
図 : 巡回セールスマン問題
上図の場合、都市の個数は 6 つあるので、巡路の総数は (6 - 1)! / 2 = 60 通りしかありません。これならば総当りで簡単に答えを求めることができます。ところが、都市の個数が多くなると簡単ではありません。n 個の都市の場合は (n - 1)! / 2 の巡路を調べなくてはいけません。巡路の総数が n の階乗に比例して増えるというのは、まさに爆発的に増えるので、n が増えると厳密解を求めるのは大変困難になります。
今回は PuLP を使って、巡回セールスマン問題を解いてみましょう。
●プログラムの作成
今回は拙作のページ「Algorithms with Python: 巡回セールスマン問題 [4]」で作成したプログラムと同様に、標準入力からデータを読み込むことにします。あとのプログラムは拙作のページ「ハミルトン閉路」で作成したものとほぼ同じですが、目的関数を設定して最小値を求めるように修正します。プログラムは次のようになります。
リスト : 巡回セールスマン問題
import sys, math, time
import pulp
# 標準入力よりデータを読み込む
def read_data():
buff = []
for a in sys.stdin:
b = a.split()
buff.append((int(b[0]), int(b[1])))
return buff
# 距離を求める
def distance(p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx * dx + dy * dy)
# 隣接行列の生成
def make_matrix(ps):
return [[distance(p1, p2) for p2 in ps] for p1 in ps]
# 解を求める
def solver(ps):
size = len(ps)
ws = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('tsp')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
us = [pulp.LpVariable('u{}'.format(i), cat='Integer', lowBound=0, upBound=size-1) \
for i in range(size)]
# 目的関数
prob += pulp.lpSum([pulp.lpDot(w, x) for w, x in zip(ws, xs)])
# 制約条件
for i in range(size):
prob += pulp.lpSum([xs[j][i] for j in range(size)]) == 1
prob += pulp.lpSum([xs[i][j] for j in range(size)]) == 1
# 自分自身への辺は選択しない
for i in range(size): prob += xs[i][i] == 0
# 頂点に対応する変数の制約
for i in range(size):
for j in range(1, size):
if i == j: continue
prob += us[i] + 1 - (size - 1) * (1 - xs[i][j]) <= us[j]
prob += us[0] == 0 # スタート
for i in range(1, size): prob += 1 <= us[i]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([int(u.value()) for u in us])
print("z", prob.objective.value())
print(time.time() - s)
# 実行
solver(read_data())
データは関数 read_data() で読み込み、それを関数 solver() に渡します。引数 ps から関数 make_matrix() で隣接行列を生成します。目的関数は拙作のページ「最短経路問題」と同じで、選択した辺の長さの合計値になります。制約条件ですが、まずは「ハミルトン閉路」と同じ条件で試してみましょう。
テストデータは拙作のページ「Algorithms with Python: 巡回セールスマン問題 [4]」と同じものを使用します。
表 : テストデータ
r19.txt r20.txt r21.txt r22.txt r23.txt
--------------------------------------------
422 295 396 162 323 424 264 95 346 106
140 324 96 38 22 396 137 222 140 414
275 118 221 336 205 19 298 156 363 298
282 64 121 380 61 116 323 136 136 268
403 324 416 85 379 156 359 364 321 31
200 335 98 296 75 320 122 283 367 367
377 417 377 78 356 96 79 235 23 428
376 80 44 400 242 423 321 358 375 428
118 40 84 61 78 421 37 59 226 312
358 58 319 380 24 222 80 382 50 388
258 81 117 278 320 257 82 320 85 27
84 380 22 103 157 245 219 119 388 396
275 402 162 381 345 199 417 245 48 328
79 60 244 417 45 121 182 379 143 382
384 320 317 120 319 185 425 102 107 112
57 242 260 256 58 77 223 282 330 336
224 60 280 202 44 184 320 18 228 300
155 316 223 61 235 375 183 155 364 167
44 305 124 119 98 299 144 283 305 308
182 263 38 216 258 220 212 45
238 305 95 165 152 21
84 423 263 352
176 258
都市の数は 19 から 23 までで、配置は乱数で決めたものです。実行結果は次のようになりました。
$ python3 tsp0.py < r19.txt Status Optimal [0, 12, 4, 3, 18, 14, 16, 1, 7, 2, 5, 11, 15, 8, 17, 9, 6, 13, 10] z 1444.0588618791196 5.065310955047607 $ python3 tsp0.py < r20.txt Status Optimal [0, 5, 17, 13, 1, 11, 2, 12, 6, 16, 10, 7, 14, 15, 3, 18, 19, 4, 8, 9] z 1672.3115177286468 13.73769497871399 $ python3 tsp0.py < r21.txt Status Optimal [0, 18, 8, 10, 6, 17, 7, 20, 19, 13, 3, 15, 5, 11, 4, 9, 12, 1, 16, 14, 2] z 1623.6108717441127 12.862587928771973 $ python3 tsp0.py < r22.txt Status Optimal [0, 16, 1, 2, 6, 14, 17, 7, 19, 12, 13, 21, 5, 10, 4, 9, 3, 20, 15, 8, 18, 11] z 1873.8983412008597 12.548322677612305 $ python3 tsp0.py < r23.txt Status Optimal [0, 12, 2, 16, 22, 3, 13, 5, 10, 14, 19, 4, 15, 11, 18, 6, 9, 1, 7, 21, 20, 8, 17] z 1694.4037091208972 7.958694696426392
表 : 実行結果
秒
: 距離 : CBC : dp
--------+--------+--------+--------
r19.txt : 1444.1 : 5.06 : 13.19
r20.txt : 1672.3 : 13.74 : 28.01
r21.txt : 1623.6 : 12.86 : 61.87
r22.txt : 1873.9 : 12.55 : 135.79
r23.txt : 1694.4 : 7.96 : ----
- 実行環境 : Python 3.10.6, PuLP 2.7.0, Ubunts 22.04 LTS (WSL2, Windows 10), Intel Core i5-6200U 2.30GHz
dp は巡回セールスマン問題 [4] で作成した動的計画法のプログラムで厳密解を求めた時の実行時間です。r23.txt の場合、時間がかかりすぎたので、途中であきらめました。Python 3.8.10 (WSL1) で実行したときは約 5 分で解くことができました。MTZ 方式の制約はまだ弱いのですが、それでも dp よりは速くなりました。そこで、参考 URL 5 『Python を用いた最適化ソルバー Gurobi 入門』を参考に、MTZ 方式の制約を強化してみましょう。
●MTZ 方式の強化
MTZ 方式は 辺 \(X_{ij}\) (i -> j) を使った制約式ですが、 ここに辺 \(X_{ji}\) (j -> i) の条件を加えます。次の式を見てください。
\(X_{ji}\) が 0 の場合、式 2 は (a) または (b) になります。これは式 1 と同じ制約ですね。次に \(X_{ji}\) が 1 の場合を考えます。\(X_{ij}\) が 0 であれば、式 2 は \(us[i] \leq us[j] + 1\) (c) となります。j -> i に行く辺を選ぶのですから、\(us[i]\) の値は \(us[j] + 1\) になるので式 (c) を満たします。
最後に、\(X_{ij}\) と \(X_{ji}\) が 1 の場合を考えます (式 (d))。\(us[i]\) が最小値の 1 のとき、式 (d) は \(size - 1 \leq us[j]\) になるので条件を満たしますが、それ以外の値では条件を満たさないことがわかります。つまり、\(X_{ij}\) と \(X_{ji}\) は同時に選ぶことはできない、という制約を表していると考えることができます。
\(\begin{array}{lll}
1. & us[i] + 1 - (size - 1) \times (1 - xs[i][j]) \leq us[j] & (j \ne 0, i \ne j) \\
2. & us[i] + 1 - (size - 1) \times (1 - xs[i][j]) + (size - 3) \times xs[j][i] \leq us[j] & (i, j \ne 0, i \ne j)
\end{array}\)
\(\begin{array}{lll}
(a) & X_{ij} = 0, X_{ji} = 0 & us[i] + 2 - size \leq us[j] \\
(b) & X_{ij} = 1, X_{ji} = 0 & us[i] + 1 \leq us[j] \\
(c) & X_{ij} = 0, X_{ji} = 1 & us[i] + 1 - size + 1 + size - 3 \leq us[j] \\
& & us[i] \leq us[j] + 1 \\
(d) & X_{ij} = 1, X_{ji} = 1 & us[i] + 1 + size - 3 \leq us[j] \\
& & us[i] + size - 2 \leq us[j]
\end{array}\)
プログラムの修正は簡単ですが、MTZ 方式の制約を設定するとき、for ループの変数 i も 0 を除外することをお忘れなく。
それでは、実行してみましょう。
$ python3 tsp1.py < r19.txt Status Optimal z 1444.0588618791196 [0, 12, 4, 3, 18, 14, 16, 1, 7, 2, 5, 11, 15, 8, 17, 9, 6, 13, 10] 0.8493046760559082 $ python3 tsp1.py < r20.txt Status Optimal z 1672.3115177286468 [0, 5, 17, 13, 1, 11, 2, 12, 6, 16, 10, 7, 14, 15, 3, 18, 19, 4, 8, 9] 3.683788776397705 $ python3 tsp1.py < r21.txt Status Optimal z 1623.6108717441127 [0, 18, 8, 10, 6, 17, 7, 20, 19, 13, 3, 15, 5, 11, 4, 9, 12, 1, 16, 14, 2] 3.900728225708008 $ python3 tsp1.py < r22.txt Status Optimal z 1873.8983412008597 [0, 6, 21, 20, 16, 8, 5, 15, 3, 10, 9, 1, 17, 12, 18, 13, 19, 2, 7, 14, 4, 11] 1.4932434558868408 $ python3 tsp1.py < r23.txt Status Optimal z 1694.4037091208972 [0, 11, 21, 7, 1, 20, 10, 18, 13, 9, 4, 19, 8, 12, 5, 17, 14, 22, 16, 2, 3, 15, 6] 4.677115201950073
表 : 実行結果
秒
: 距離 : MTZ0 : MTZ1
--------+--------+--------+--------
r19.txt : 1444.1 : 5.06 : 0.85
r20.txt : 1672.3 : 13.74 : 3.68
r21.txt : 1623.6 : 12.86 : 3.90
r22.txt : 1873.9 : 12.55 : 1.49
r23.txt : 1694.4 : 7.96 : 4.68
MTZ 方式の制約を強化することで、実行時間を短縮することができました。
●MTZ 方式の強化 (2)
制約式の強化はこれだけではありません。us[i] (i != 0) の範囲は 1 から size - 1 までですが、ここにも辺 \(X_{ij}\) と \(X_{ji}\) を使った制約を追加することができます。次の式を見てください。
\(\begin{array}{ll}
1. & 1 \leq U_{i} \leq size - 1, \ (i \ne 0) \\
2a.& 1 + (1 - X_{0i}) + (size - 3) \times X_{i0} \leq U_{i} \\
2b.& U_{i} \leq (size - 1) - (1 - X_{i0}) - (size - 3) \times X_{0i}
\end{array}\)
式 2a は \(U_{i}\) の下界を表し、式 2b は上界を表しています。まず最初に、式 2a から説明しましょう。次の式を見てください。
\(\begin{array}{lll}
a. & X_{0i} = 0, X_{i0} = 0 & 2 \leq U_{i} \\
b. & X_{0i} = 1, X_{i0} = 0 & 1 \leq U_{i} \\
c. & X_{0i} = 0, X_{i0} = 1 & size - 1 \leq U_{i} \\
d. & X_{0i} = 1, X_{i0} = 1 & size - 2 \leq U_{i}
\end{array}\)
辺 \(X_{0i}\) は最初に選択する辺、\(X_{i0}\) は最後に選択する辺を表します。a の場合、\(X_{0i}\) は 0 なので、\(U_{i}\) は 2 以上であることがわかります。b の場合、\(X_{0i}\) は 1 なので、\(U_{i}\) は 1 になります。c の場合、\(X_{i0}\) は 1 なので、\(U_{i}\) の値は size - 1 となります。d の場合、最後に選択する辺は条件を満たしますが、最初に選択する辺は条件を満たしません。つまり、2 つの辺を同時に選ぶことはできないわけです。
次に式 2b を説明します。
\(\begin{array}{lll}
a. & X_{0i} = 0, X_{i0} = 0 & U_{i} \leq size - 2 \\
b. & X_{0i} = 1, X_{i0} = 0 & U_{i} \leq 1 \\
c. & X_{0i} = 0, X_{i0} = 1 & U_{i} \leq size - 1 \\
d. & X_{0i} = 1, X_{i0} = 1 & U_{i} \leq 2
\end{array}\)
a の場合、\(X_{i0}\) は 0 なので、\(U_{i}\) の値は size - 2 以下になります。b の場合、\(X_{0i}\) は 1 なので、\(U_{i}\) の値は 1 になります。c の場合、\(X_{i0}\) が 1 なので、\(U_{i}\) の値は size - 1 となります。d の場合、最初に選択する辺は条件を満たしていますが、最後に選択する辺は条件を満たしません。つまり、2 つの辺を同時に選ぶことはできないわけです。
以上の制約条件を設定するプログラムは次のようになります。
リスト : 制約条件の設定
# 頂点に対応する変数の制約
for i in range(1, size):
for j in range(1, size):
if i == j: continue
prob += us[i] + 1 - size * (1 - xs[i][j]) + (size - 3) * xs[j][i] <= us[j]
# 上界と下界の制約
for i in range(1, size):
prob += 1 + (1 - xs[0][i]) + (size - 3) * xs[i][0] <= us[i]
prob += us[i] <= (size - 1) - (1 - xs[i][0]) - (size - 3) * xs[0][i]
制約条件の式をそのままプログラムしただけなので、とくに難しいところはないと思います。
それでは実行してみましょう。
$ python3 tsp2.py < r19.txt Status Optimal z 1444.0588618791196 [0, 12, 4, 3, 18, 14, 16, 1, 7, 2, 5, 11, 15, 8, 17, 9, 6, 13, 10] 0.36330270767211914 $ python3 tsp2.py < r20.txt Status Optimal z 1672.3115177286468 [0, 5, 17, 13, 1, 11, 2, 12, 6, 16, 10, 7, 14, 15, 3, 18, 19, 4, 8, 9] 1.5430612564086914 $ python3 tsp2.py < r21.txt Status Optimal z 1623.610871744113 [0, 3, 13, 11, 15, 4, 14, 1, 2, 8, 18, 6, 16, 10, 17, 12, 9, 20, 5, 7, 19] 1.1122725009918213 $ python3 tsp2.py < r22.txt Status Optimal z 1873.8983412008597 [0, 16, 1, 2, 6, 14, 17, 7, 19, 12, 13, 21, 5, 10, 4, 9, 3, 20, 15, 8, 18, 11] 0.48087644577026367 $ python3 tsp2.py < r23.txt Status Optimal z 1694.4037091208972 [0, 12, 2, 16, 22, 3, 13, 5, 10, 14, 19, 4, 15, 11, 18, 6, 9, 1, 7, 21, 20, 8, 17] 2.641566753387451
表 : 実行結果
秒
: 距離 : MTZ0 : MTZ1 : MTZ2
--------+--------+--------+--------+--------
r19.txt : 1444.1 : 5.06 : 0.85 : 0.36
r20.txt : 1672.3 : 13.74 : 3.68 : 1.54
r21.txt : 1623.6 : 12.86 : 3.90 : 1.11
r22.txt : 1873.9 : 12.55 : 1.49 : 0.48
r23.txt : 1694.4 : 7.96 : 4.68 : 2.64
上界と下界の制約を強化した効果はとても大きいですね。最適化ソルバーを使う場合、適切な制約条件を設定することがいかに重要であるか、実感することができました。
ご参考までに、都市を 30 から 35 に増やして実行してみました。都市のデータはプログラムリストの中に記述してあります。興味のある方はいろいろ試してみてください。
- 都市 = 30
Status Optimal z 2107.1164165203804 [0, 9, 6, 16, 23, 10, 11, 5, 21, 3, 2, 12, 20, 28, 1, 22, 8, 13, 17, 4, 25, 14, 24, 27, 18, 19, 29, 26, 7, 15] 5.7379536628723145
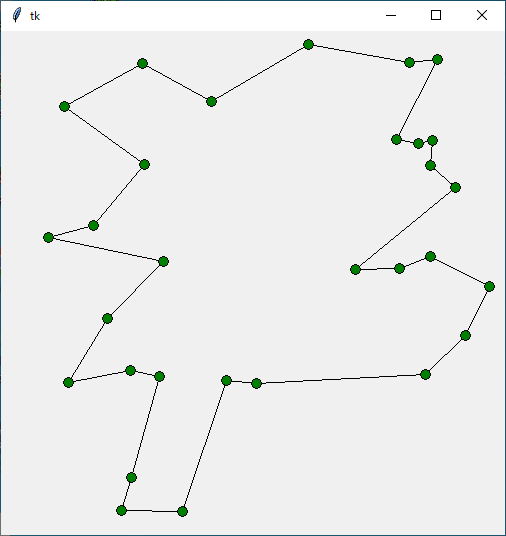
Status Optimal z 2109.987751296947 [0, 11, 13, 25, 15, 12, 6, 24, 21, 2, 3, 16, 18, 30, 29, 28, 20, 27, 8, 17, 4, 14, 26, 23, 1, 22, 19, 9, 10, 5, 7] 1.908207893371582
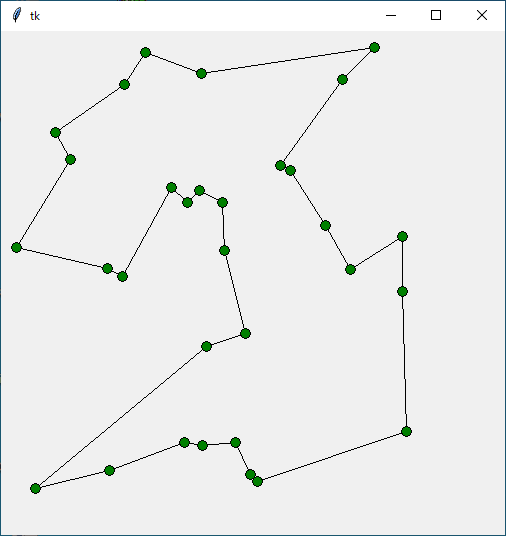
Status Optimal z 2000.4848173951339 [0, 9, 13, 20, 15, 25, 12, 21, 19, 6, 16, 10, 30, 4, 14, 1, 26, 8, 28, 11, 24, 31, 18, 17, 3, 27, 29, 23, 2, 22, 7, 5] 0.6576001644134521
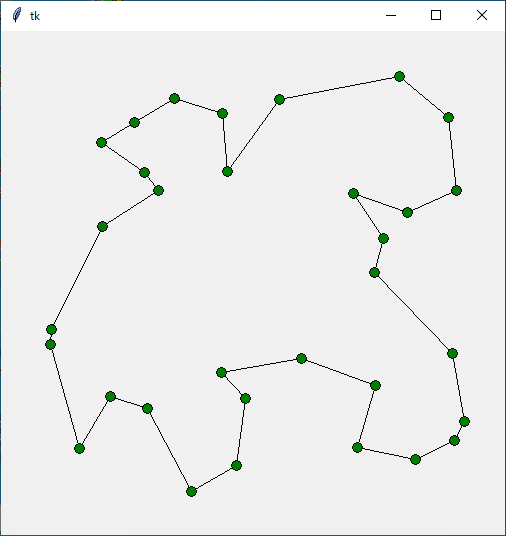
Status Optimal z 2407.4327709030326 [0, 6, 10, 15, 4, 27, 30, 29, 31, 19, 5, 1, 17, 2, 3, 12, 32, 13, 25, 8, 22, 21, 18, 14, 16, 24, 26, 28, 23, 9, 11, 7, 20] 61.740641832351685
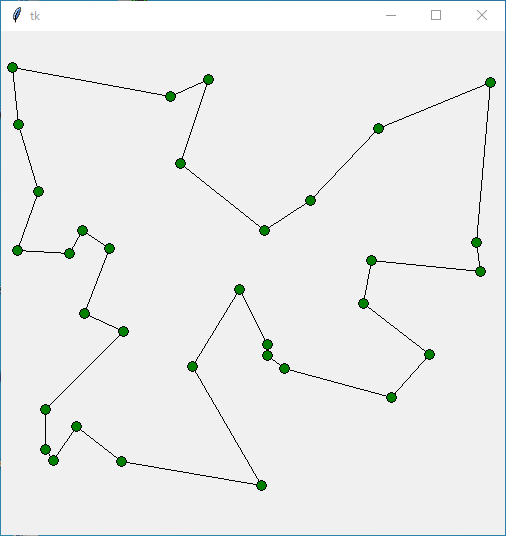
Status Optimal z 2318.344547552223 [0, 10, 18, 5, 9, 24, 12, 23, 1, 14, 19, 3, 30, 28, 27, 33, 4, 16, 13, 20, 26, 8, 2, 31, 29, 15, 7, 21, 11, 17, 6, 22, 25, 32] 3.7241899967193604
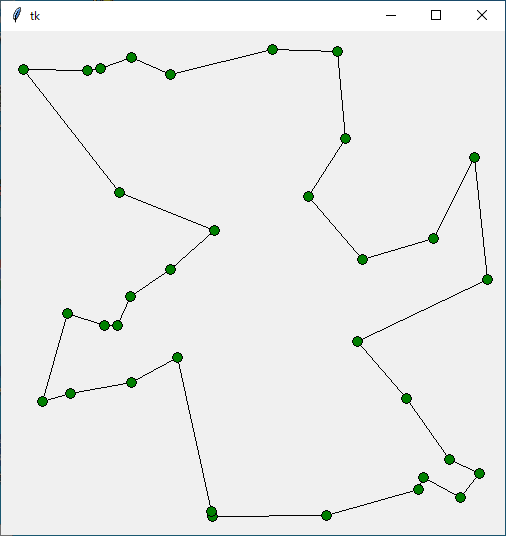
Status Optimal z 2332.18624211698 [0, 24, 28, 13, 31, 17, 3, 1, 11, 6, 2, 10, 5, 25, 32, 30, 23, 19, 22, 34, 9, 7, 14, 20, 27, 21, 18, 29, 8, 16, 26, 15, 33, 12, 4] 6.1202712059021
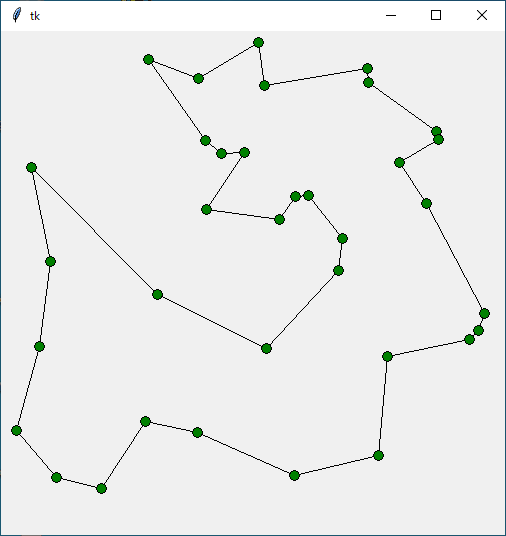
表 : 実行結果
都市 : 距離 : 秒
------+--------+-------
30 : 2107.1 : 5.75
31 : 2110.0 : 1.91
32 : 2000.5 : 0.66
33 : 2407.4 : 61.74
34 : 2318.3 : 3.72
35 : 2332.2 : 6.12
●プログラムリスト
#
# tsp.py : PuLP による巡回セールスマン問題の解法
#
# Copyright (C) 2019-2023 Makoto Hiroi
#
import sys, math, time, random
import pulp
import tkinter as tk
# 乱数でデータを生成
def make_data(n):
return [(random.randrange(480) + 10, random.randrange(480) + 10) for _ in range(n)]
# 描画
def draw(ps, xs):
root = tk.Tk()
c0 = tk.Canvas(root, width = 500, height = 500)
c0.pack()
for i in range(len(xs)):
for j in range(len(xs)):
if xs[i][j].value() == 0: continue
c0.create_line(ps[i][0], ps[i][1], ps[j][0], ps[j][1], width = 1.0)
for i, j in ps:
c0.create_oval(i - 5, j - 5, i + 5, j + 5, fill = 'green')
root.mainloop()
# 標準入力よりデータを読み込む
def read_data():
buff = []
for a in sys.stdin:
b = a.split()
buff.append((int(b[0]), int(b[1])))
return buff
# 距離を求める
def distance(p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx * dx + dy * dy)
# 隣接行列の生成
def make_matrix(ps):
return [[distance(p1, p2) for p2 in ps] for p1 in ps]
# 解を求める
def solver(ps):
size = len(ps)
ws = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('tsp')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
us = [pulp.LpVariable('u{}'.format(i), cat='Integer', lowBound=0, upBound=size-1) \
for i in range(size)]
# 目的関数
prob += pulp.lpSum([pulp.lpDot(w, x) for w, x in zip(ws, xs)])
# 制約条件
for i in range(size):
prob += pulp.lpSum([xs[j][i] for j in range(size)]) == 1
prob += pulp.lpSum([xs[i][j] for j in range(size)]) == 1
# 自分自身への辺は選択しない
for i in range(size): prob += xs[i][i] == 0
# 頂点に対応する変数の制約
for i in range(1, size):
for j in range(1, size):
if i == j: continue
prob += us[i] + 1 - size * (1 - xs[i][j]) + (size - 3) * xs[j][i] <= us[j]
# 上界と下界の制約
for i in range(1, size):
prob += 1 + (1 - xs[0][i]) + (size - 3) * xs[i][0] <= us[i]
prob += us[i] <= (size - 1) - (1 - xs[i][0]) - (size - 3) * xs[0][i]
prob += us[0] == 0 # スタート
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print([int(u.value()) for u in us])
print(time.time() - s)
# Tkinter による描画
# draw(ps, xs)
# データ
ps30 = [(255, 352), (431, 109), (354, 238), (141, 32), (67, 351), (417, 112), (395, 108),
(398, 237), (162, 230), (488, 255), (464, 304), (436, 28), (47, 206), (181, 480),
(424, 343), (106, 287), (429, 134), (408, 31), (63, 75), (429, 225), (158, 345),
(307, 13), (129, 339), (120, 479), (143, 133), (92, 194), (225, 349), (130, 446),
(454, 156), (210, 70)]
ps31 = [(183, 411), (279, 134), (373, 16), (221, 171), (144, 21), (341, 48), (401, 260),
(198, 159), (121, 245), (234, 411), (249, 443), (123, 53), (69, 128), (108, 439),
(34, 457), (205, 315), (106, 237), (244, 302), (349, 238), (54, 101), (256, 450),
(200, 42), (223, 219), (186, 171), (201, 414), (170, 156), (15, 216), (324, 194),
(289, 139), (405, 400), (401, 205)]
ps32 = [(221, 82), (78, 417), (235, 434), (453, 409), (220, 341), (352, 162), (190, 460),
(463, 390), (414, 428), (101, 195), (300, 327), (109, 365), (278, 68),
(143, 141), (244, 367), (173, 67), (406, 181), (49, 313), (447, 86), (146, 377),
(382, 207), (226, 140), (356, 416), (374, 354), (100, 111), (455, 159),
(398, 45), (373, 241), (133, 91), (451, 322), (50, 298), (157, 159)]
ps33 = [(17, 93), (83, 282), (52, 429), (238, 258), (81, 199), (309, 169), (207, 48),
(179, 132), (169, 65), (390, 366), (108, 217), (37, 160), (266, 324), (16, 219),
(68, 222), (120, 430), (11, 36), (260, 454), (489, 51), (44, 378), (370, 229),
(362, 272), (283, 337), (191, 335), (266, 313), (475, 211), (377, 97),
(263, 199), (479, 240), (44, 418), (75, 395), (122, 300), (428, 323)]
ps34 = [(271, 18), (448, 428), (176, 326), (432, 207), (405, 367), (116, 294),
(459, 466), (103, 294), (336, 20), (417, 458), (130, 351), (307, 165),
(86, 39), (118, 161), (213, 199), (169, 43), (361, 228), (211, 485), (422, 446),
(69, 362), (169, 238), (356, 310), (344, 107), (99, 37), (22, 38), (325, 484),
(486, 248), (41, 370), (478, 442), (210, 480), (473, 126), (66, 282),
(129, 265), (130, 26)]
ps35 = [(341, 207), (196, 401), (15, 399), (367, 51), (30, 136), (425, 172), (278, 188),
(307, 164), (263, 54), (220, 122), (294, 165), (257, 11), (243, 121),
(144, 390), (156, 263), (49, 230), (293, 444), (477, 299), (377, 424),
(337, 239), (197, 47), (204, 109), (435, 100), (468, 308), (55, 446), (386, 325),
(483, 282), (38, 315), (147, 28), (398, 131), (100, 457), (437, 108), (265, 317),
(366, 37), (205, 178)]
# 実行
for ps in [ps30, ps31, ps32, ps33, ps34, ps35]:
solver(ps)
●フロー型部分巡回路除去制約
今回は flow formulation (単品種フロー) と呼ばれる部分巡回路除去制約を紹介します。セールスマンは「もの」を所持していて、都市を訪問するたびに「もの」を一つ置いていきます。n 個の都市を巡回するのであれば、セールスマンは n 個の「もの」を持っていて、都市を移動するたびに持っている「もの」は一つずつ減っていきます。セールスマンが運ぶ「もの」の個数をフローとみなして定式化するのが単品種フローの考え方です。
簡単な例を示しましょう。次の図を見てください。
: A B C D
A -- 3 -- B ---+-------------
| | A : X 3 0 0
0 2 B : 0 X 2 0
| | C : 0 0 X 1
D -- 1 -- C D : 0 0 0 X
都市 A から出発して B, C, D の順番で巡回します。都市 i から j にを移動するときサラリーマンが持っている「もの」の個数を \(f_{ij}\) とすると、\(f_{AB} = 3, f_{BC} = 2, f_{CD} = 1, f_{DA} = 0\) になります。これを表にすると上図 (右) のようになり、次式に示すような関係が成り立ちます。
\(\begin{array}{l}
(f_{AB} + f_{AC} + f_{AD}) - (f_{BA} + f_{CA} + f_{DA}) = 3 \\
(f_{BA} + f_{BC} + f_{BD}) - (f_{AB} + f_{CB} + f_{DB}) = -1 \\
(f_{CA} + f_{CB} + f_{CD}) - (f_{AC} + f_{BC} + f_{DC}) = -1 \\
(f_{DA} + f_{DB} + f_{DC}) - (f_{AD} + f_{BD} + f_{CD}) = -1
\end{array}\)
出発点 A を除いて、頂点から流出するフローから流入するフローを引き算すると -1 になります。出発点は特別で、都市の個数を n とすると、フローの差は n - 1 になります。
フローを表す変数 \(f_{ij}\) を使って制約条件を記述すると次のようになります。
\(\begin{array}{l}
\displaystyle \sum_{j=1} f_{0j} - \sum_{j=1} f_{j0} = n - 1 \\
\displaystyle \sum_{j=0} f_{ij} - \sum_{j=1} f_{ji} = -1, \quad (i \ne 0, j \ne i)
\end{array}\)
このほかにも、変数 \(f_{ij}\) には制約条件があります。\(f_{ij}\) の値は、辺 \(X_{ij}\) が 1 であれば n - 1 以下になり、\(X_{ij}\) が 0 であれば 0 になります。したがって、制約条件は次式のようになります。
\(
0 \leq f_{ij} \leq (n - 1) \times X_{ij}
\)
あとはこれを PuLP でプログラムするだけです。次のリストを見てください。
リスト : 単品種フロー型部分巡回路除去制約
def solver(ps):
size = len(ps)
ws = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('tsp')
# 変数の生成
xs = []
fs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs1 = [pulp.LpVariable('f{}_{}'.format(i, j), cat='Integer', lowBound=0) for j in range(size)]
fs.append(fs1)
# 目的関数
prob += pulp.lpSum([pulp.lpDot(w, x) for w, x in zip(ws, xs)])
# 制約条件
for i in range(size):
prob += pulp.lpSum([xs[j][i] for j in range(size)]) == 1
prob += pulp.lpSum([xs[i][j] for j in range(size)]) == 1
# 自分自身への辺は選択しない
for i in range(size): prob += xs[i][i] == 0
# 単品種フロー型部分巡回路除去制約
for i in range(size):
for j in range(size):
if i == j: continue
prob += fs[i][j] <= (size - 1) * xs[i][j]
prob += pulp.lpSum([fs[0][i] for i in range(1, size)]) \
- pulp.lpSum([fs[i][0] for i in range(1, size)]) == size - 1
for i in range(1, size):
prob += pulp.lpSum([fs[i][j] for j in range(size) if i != j]) \
- pulp.lpSum([fs[j][i] for j in range(size) if i != j]) == - 1
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
# draw(ps, xs)
フロー \(f_{ij}\) を表す変数は配列 fs に格納します。あとは制約条件をそのままプログラムしただけなので、とくに難しいところはないと思います。
実行結果を示します。
表 : 実行結果
秒
: 距離 : MTZ0 : MTZ1 : MTZ2 : FLOW
--------+--------+--------+--------+--------+-------
r19.txt : 1444.1 : 5.06 : 0.85 : 0.36 : 1.33
r20.txt : 1672.3 : 13.74 : 3.68 : 1.54 : 2.37
r21.txt : 1623.6 : 12.86 : 3.90 : 1.11 : 0.82
r22.txt : 1873.9 : 12.55 : 1.49 : 0.48 : 4.80
r23.txt : 1694.4 : 7.96 : 4.68 : 2.64 : 3.14
単品種フロー (FLOW) は MTZ 方式で制約を強化していない MTZ0 よりも高速ですが、強化版である MTZ2 よりも遅くなる場合が多いようです。そこで、単品種フローの制約をもう少しだけ強化してみましょう。
●制約の強化
制約の強化は簡単です。変数 \(f_{ij}\) の値が n - 1 になるのは i が 0 のときだけです。それ以外の変数の値は n - 2 以下になります。これを制約として追加しましょう。プログラムの修正も簡単です。次のリストを見てください。
リスト : 制約の強化
for i in range(1, size):
prob += fs[0][i] <= (size - 1) * xs[0][i]
for i in range(1, size):
for j in range(size):
if i == j: continue
prob += fs[i][j] <= (size - 2) * xs[i][j]
fs[0][i] の上限値を (size - 1) * xs[0][i] とし、それ以外の変数 fs[i][j] の上限値は (size - 2) * xs[i][j] とするだけです。
実行結果は次のようになりました。
表 : 実行結果
秒
: 距離 : MTZ0 : MTZ1 : MTZ2 : FLOW : FLOW1
--------+--------+--------+--------+--------+--------+--------
r19.txt : 1444.1 : 5.06 : 0.85 : 0.36 : 1.33 : 0.45
r20.txt : 1672.3 : 13.74 : 3.68 : 1.54 : 2.37 : 1.14
r21.txt : 1623.6 : 12.86 : 3.90 : 1.11 : 0.82 : 1.43
r22.txt : 1873.9 : 12.55 : 1.49 : 0.48 : 4.80 : 5.82
r23.txt : 1694.4 : 7.96 : 4.68 : 2.64 : 3.14 : 2.11
データによって効果はまちまちですが、制約を強化したことにより MTZ2 よりも速くなる場合もあるようです。制約式によって得手不得手があるのかもしれません。ご参考までに都市の数を 30 から 35 に増やしたときの実行結果を示します。
表 : 実行結果
都市 : 距離 : MTZ : FLOW : FLOW1
------+--------+-------+-------+--------
30 : 2107.1 : 5.75 : 11.84 : 5.12
31 : 2110.0 : 1.91 : ---- : 44.61
32 : 2000.5 : 0.66 : 15.89 : 6.05
33 : 2407.4 : 61.74 : 73.26 : 44.32
34 : 2318.3 : 3.72 : 23.41 : 102.92
35 : 2332.2 : 6.12 : ---- : 215.68
FLOW の 31, 35 都市は時間がかかりすぎるため、途中であきらめました。都市の個数が増えると、MTZ 方式のほうが速いですね。興味のある方はいろいろ試してみてください。
●参考 URL
- 汎用MIPソルバによる巡回セールスマン問題の求解 : 多項式オーダ本数の部分巡回路除去制約 [PDF], (沼田一道さん)
- ロジスティクス工学 07 配送計画, (宮本裕一郎さん)
●プログラムリスト
リスト : 制約式の強化
def solver(ps):
size = len(ps)
ws = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('tsp')
# 変数の生成
xs = []
fs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs1 = [pulp.LpVariable('f{}_{}'.format(i, j), cat='Integer', lowBound=0) for j in range(size)]
fs.append(fs1)
# 目的関数
prob += pulp.lpSum([pulp.lpDot(w, x) for w, x in zip(ws, xs)])
# 制約条件
for i in range(size):
prob += pulp.lpSum([xs[j][i] for j in range(size)]) == 1
prob += pulp.lpSum([xs[i][j] for j in range(size)]) == 1
# 自分自身への辺は選択しない
for i in range(size): prob += xs[i][i] == 0
# 単品種フロー型部分巡回路除去制約 (強化版)
for i in range(1, size):
prob += fs[0][i] <= (size - 1) * xs[0][i]
for i in range(1, size):
for j in range(size):
if i == j: continue
prob += fs[i][j] <= (size - 2) * xs[i][j]
prob += pulp.lpSum([fs[0][i] for i in range(1, size)]) \
- pulp.lpSum([fs[i][0] for i in range(1, size)]) == size - 1
for i in range(1, size):
prob += pulp.lpSum([fs[i][j] for j in range(size) if i != j]) \
- pulp.lpSum([fs[j][i] for j in range(size) if i != j]) == - 1
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
# draw(ps, xs)