●最大フロー問題
「最大フロー問題 (Maximum flow problem)」または「最大流問題」とは、ネットワーク上でソース (供給点) からシンク (需要点) まで流すことができる「もの」の最大値を求める問題です。ソースから流れ出したものは、辺と頂点を経由してシンクに流入しますが、このとき次に示す制約条件を満たさなければなりません。
- 各辺には容量があり、それ以上の量を流すことはできない
- ソースとシンク以外の頂点において、流入する総量と流出する総量は等しい (保存則)
最大フロー問題は昔からいろいろな解法アルゴリズムが考案されていますが、線形計画法でも解くことが可能です。簡単な例題として、下図に示す有効グラフ (出典: 参考 URL 1 『最適化基礎 第9回 最大流問題と増加路アルゴリズム』) において、A から F までの最大フローを求めてみましょう。
辺 : 容量
-------+------
Ｂ─────Ｄ A -> B : 5
／│ ／│＼ A -> C : 2
／ │ ／ │ ＼ B -> C : 6
Ａ │ ／ │ Ｆ B -> D : 4
＼ │ ／ │ ／ C -> D : 2
＼│／ │／ C -> E : 3
Ｃ─────Ｅ D -> E : 3
D -> F : 1
E -> F : 9
図 : 有向グラフ
総量を f とし、辺 i -> j に対応する変数を \(X_{ij}\) とすると、目的関数と制約条件は次式のようになります。
1. 辺の容量
\(\begin{array}{l} 0 \leq X_{ab} \leq 5 \\ 0 \leq X_{ac} \leq 2 \\ 0 \leq X_{bc} \leq 6 \\ 0 \leq X_{bd} \leq 4 \\ 0 \leq X_{cd} \leq 2 \\ 0 \leq X_{ce} \leq 3 \\ 0 \leq X_{de} \leq 3 \\ 0 \leq X_{df} \leq 1 \\ 0 \leq X_{ef} \leq 9 \end{array}\)
2. 各頂点の保存則
\(\begin{array}{ll} B & X_{ab} = X_{bd} + X_{bc} \\ C & X_{ac} + X_{bc} = X_{cd} + X_{ce} \\ D & X_{bd} + X_{cd} = X_{de} + X_{df} \\ E & X_{ce} + X_{de} = X_{ef} \end{array}\)
あとはこれを PuLP でそのままプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 最大フロー問題
import pulp
prob = pulp.LpProblem('max-flow', sense = pulp.LpMaximize)
# 変数
xab = pulp.LpVariable('xab', lowBound = 0, upBound = 5)
xac = pulp.LpVariable('xac', lowBound = 0, upBound = 2)
xbc = pulp.LpVariable('xbc', lowBound = 0, upBound = 6)
xbd = pulp.LpVariable('xbd', lowBound = 0, upBound = 4)
xcd = pulp.LpVariable('xcd', lowBound = 0, upBound = 2)
xce = pulp.LpVariable('xce', lowBound = 0, upBound = 3)
xde = pulp.LpVariable('xde', lowBound = 0, upBound = 3)
xdf = pulp.LpVariable('xdf', lowBound = 0, upBound = 1)
xef = pulp.LpVariable('xef', lowBound = 0, upBound = 9)
# 目的関数
prob += xab + xac
# 制約条件
prob += xab == xbc + xbd
prob += xac + xbc == xcd + xce
prob += xbd + xcd == xde + xdf
prob += xce + xde == xef
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print('xab =', xab.value())
print('xac =', xac.value())
print('xbc =', xbc.value())
print('xbd =', xbd.value())
print('xcd =', xcd.value())
print('xce =', xce.value())
print('xde =', xde.value())
print('xdf =', xdf.value())
print('xef =', xef.value())
print("f", prob.objective.value())
Status Optimal xab = 5.0 xac = 2.0 xbc = 1.0 xbd = 4.0 xcd = 0.0 xce = 3.0 xde = 3.0 xdf = 1.0 xef = 6.0 f 7.0
結果は 7 になりました。ところで、今回のプログラムは変数を一つずつ定義しましたが、Python の内包表記を使って変数を辞書に格納することもできます。ご参考までに、プログラムリストと実行結果を示します。
リスト ; 最大フロー問題 (2)
import pulp
prob = pulp.LpProblem('max-flow', sense = pulp.LpMaximize)
# 辺
es = ['ab', 'ac', 'bc', 'bd', 'cd', 'ce', 'de', 'df', 'ef']
# 容量
ws = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# 変数
vs = {e: pulp.LpVariable('x{}'.format(e), lowBound = 0, upBound = w) for e, w in zip(es, ws)}
# 目的関数
prob += vs['ab'] + vs['ac']
# 制約条件
prob += vs['ab'] == vs['bc'] + vs['bd']
prob += vs['ac'] + vs['bc'] == vs['cd'] + vs['ce']
prob += vs['bd'] + vs['cd'] == vs['de'] + vs['df']
prob += vs['ce'] + vs['de'] == vs['ef']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es:
print(e, vs[e].value())
print("f", prob.objective.value())
Status Optimal ab 5.0 ac 2.0 bc 1.0 bd 4.0 cd 0.0 ce 3.0 de 3.0 df 1.0 ef 6.0 f 7.0
●参考 URL
- 最適化基礎 第9回 最大流問題と増加路アルゴリズム [PDF], (塩浦昭義さん)
- 最大フロー問題 - Wikipedia
●最小カット問題
有向グラフの頂点の集合 V をソース側の集合 S とシンク側の集合 T に分けることを「s - t カット」といいます。このとき、S から T に向かう辺の容量の総和を「カットの容量」といいます。最小カット問題は、カットの容量が最小となる分割の仕方を求める問題です。ようするに、ソースからシンクにものが流れなくなるような辺の切断の仕方で、切断する辺の容量の総和が最小となる組み合わせを求める問題、ということになります。
最小カット問題にも高速な解法アルゴリズムが考案されていますが、線形計画法でも解くことが可能です。最小カット問題の定式化については、参考 URL 『数理計画法 第９回 ネットワーク計画 非線形計画』の説明がわかりやすいと思います。講義資料を公開されている塩浦昭義先生に感謝いたします。
頂点に対応する変数を \(V_i\) とし、辺 (i -> j) に対応する変数を \(X_{ij}\) とします。\(V_i\) の値はソース側に属していれば 0 とし、シンク側に属していれば 1 とします。\(X_{ij}\) は切断する辺であれば 1 とし、そうでなければ 0 とします。すると、目的関数と制約条件は次のようになります。
\( \displaystyle \sum_{i,j} W_{ij} X_{ij} \)
\(W_{ij}\) は辺 (i -> j) の容量
\( V_i - V_j + X_{ij} \geq 0 \)
目的関数は簡単ですね。制約条件ですが、\(V_{i}\) がシンク側で \(V_{j}\) がソース側のときだけ \(V_{i} - V_{j}\) の値は -1 になります。したがって、制約条件を満たすには \(X_{ij}\) を 1 としなければなりません。それ以外の場合は \(X_{ij}\) が 0 でも 1 でも条件を満たしますが、目的関数は最小化されるので \(X_{ij}\) の値は 0 になります。これで最小カットと切断する辺を求めることができます。
それでは、拙作のページ「最大フロー問題」と同じ有向グラフで最小カットを求めてみましょう。プログラムは次のようになります。
リスト : 最小カット問題
import pulp
prob = pulp.LpProblem('min-cut')
# 辺
xab = pulp.LpVariable('xab', cat='Binary')
xac = pulp.LpVariable('xac', cat='Binary')
xbc = pulp.LpVariable('xbc', cat='Binary')
xbd = pulp.LpVariable('xbd', cat='Binary')
xcd = pulp.LpVariable('xcd', cat='Binary')
xce = pulp.LpVariable('xce', cat='Binary')
xde = pulp.LpVariable('xde', cat='Binary')
xdf = pulp.LpVariable('xdf', cat='Binary')
xef = pulp.LpVariable('xef', cat='Binary')
xs = [xab, xac, xbc, xbd, xcd, xce, xde, xdf, xef]
# 重み
ws = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# 頂点
va = pulp.LpVariable('va', cat='Binary')
vb = pulp.LpVariable('vb', cat='Binary')
vc = pulp.LpVariable('vc', cat='Binary')
vd = pulp.LpVariable('vd', cat='Binary')
ve = pulp.LpVariable('ve', cat='Binary')
vf = pulp.LpVariable('vf', cat='Binary')
vs = [va, vb, vc , vd, ve, vf]
# 目的関数
prob += pulp.lpDot(ws, xs)
# 制約条件
prob += va == 0
prob += vf == 1
prob += va - vb + xab >= 0
prob += va - vc + xac >= 0
prob += vb - vc + xbc >= 0
prob += vb - vd + xbd >= 0
prob += vc - vd + xcd >= 0
prob += vc - ve + xce >= 0
prob += vd - ve + xde >= 0
prob += vd - vf + xdf >= 0
prob += ve - vf + xef >= 0
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print('xab =', xab.value())
print('xac =', xac.value())
print('xbc =', xbc.value())
print('xbd =', xbd.value())
print('xcd =', xcd.value())
print('xce =', xce.value())
print('xde =', xde.value())
print('xdf =', xdf.value())
print('xef =', xef.value())
print("z", prob.objective.value())
Status Optimal xab = 0.0 xac = 0.0 xbc = 0.0 xbd = 0.0 xcd = 0.0 xce = 1.0 xde = 1.0 xdf = 1.0 xef = 0.0 z 7.0
最小カットは 7 になりました。これは最大フローと一致していますが偶然ではありません。最大フローと最小カットの値は一致することが証明されているそうです。これを「最大フロー最小カット定理」といいます。興味のある方は参考 URL をお読みください。
ご参考までに、Python の辞書を使ったプログラムと実行結果を示します。
リスト : 最小カット問題 (2)
import pulp
prob = pulp.LpProblem('min-cut')
# 辺
es = ['ab', 'ac', 'bc', 'bd', 'cd', 'ce', 'de', 'df', 'ef']
# 容量
ws = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# 辺の変数
xs = {e: pulp.LpVariable('x{}'.format(e), cat='Binary') for e in es}
# 頂点の変数
vs = {e: pulp.LpVariable('v{}'.format(e), cat='Binary') for e in ['a', 'b', 'c', 'd', 'e', 'f']}
# 目的関数
prob += pulp.lpDot(ws, [xs[e] for e in es])
# 制約条件
prob += vs['a'] == 0
prob += vs['f'] == 1
prob += vs['a'] - vs['b'] + xs['ab'] >= 0
prob += vs['a'] - vs['c'] + xs['ac'] >= 0
prob += vs['b'] - vs['c'] + xs['bc'] >= 0
prob += vs['b'] - vs['d'] + xs['bd'] >= 0
prob += vs['c'] - vs['d'] + xs['cd'] >= 0
prob += vs['c'] - vs['e'] + xs['ce'] >= 0
prob += vs['d'] - vs['e'] + xs['de'] >= 0
prob += vs['d'] - vs['f'] + xs['df'] >= 0
prob += vs['e'] - vs['f'] + xs['ef'] >= 0
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es:
print(e, ' =', xs[e].value())
print("z", prob.objective.value())
Status Optimal ab = 0.0 ac = 0.0 bc = 0.0 bd = 0.0 cd = 0.0 ce = 1.0 de = 1.0 df = 1.0 ef = 0.0 z 7.0
●参考 URL
- 数理計画法 第９回 ネットワーク計画 非線形計画 [PDF], (塩浦昭義さん)
- カット (グラフ理論) - Wikipedia
- 最大フロー最小カット定理 - Wikipedia
●最小費用フロー問題
ネットワーク上で決められた量の「もの」をソース (供給点) からシンク (需要点) まで流すとき、かかる費用 (コスト) が最小となる流し方を求める問題を「最小費用フロー問題」または「最小費用流問題」といいます。基本的な制約条件は最大フロー問題と同じです。
- 各辺には容量があり、それ以上の量を流すことはできない
- ソースとシンク以外の頂点において、流入する総量と流出する総量は等しい (保存則)
最小費用フロー問題は各辺に費用が定義されていて、ソースから流す量が f のとき、かかる費用が最小となる流し方を求めることになります。この問題も高速な解法アルゴリズムが考案されていますが、線形計画法でも解くことが可能です。簡単な例題として、下図に示す有効グラフ (出典 : 参考 URL 1 『最適化基礎 第11回 最小費用流問題 最大重みマッチングとオークション』) において、流量が 6 で A から F まで流すときの最小費用フローを求めてみましょう。
辺 : 容量 : 費用
-------+------+------
Ｂ─────Ｄ A -> B : 5 : 3
／│ ／│＼ A -> C : 2 : 7
／ │ ／ │ ＼ B -> C : 6 : 1
Ａ │ ／ │ Ｆ B -> D : 4 : 2
＼ │ ／ │ ／ C -> D : 2 : 9
＼│／ │／ C -> E : 3 : 1
Ｃ─────Ｅ D -> E : 3 : 7
D -> F : 1 : 8
E -> F : 9 : 4
図 : 有向グラフ
辺 i -> j の費用を Cij、そこに流れる量を変数 Xij で表すことにすると、目的関数と制約条件は次式のようになります。
\( z = \displaystyle \sum_{i,j} C_{ij} X_{ij} \)
1. 辺の容量
\(\begin{array}{l} 0 \leq X_{ab} \leq 5 \\ 0 \leq X_{ac} \leq 2 \\ 0 \leq X_{bc} \leq 6 \\ 0 \leq X_{bd} \leq 4 \\ 0 \leq X_{cd} \leq 2 \\ 0 \leq X_{ce} \leq 3 \\ 0 \leq X_{de} \leq 3 \\ 0 \leq X_{df} \leq 1 \\ 0 \leq X_{ef} \leq 9 \end{array}\)
2. 各頂点の保存則
\(\begin{array}{ll} A: & X_{ab} + X_{ac} = 6 \\ B: & X_{ab} = X_{bd} + X_{bc} \\ C: & X_{ac} + X_{bc} = X_{cd} + X_{ce} \\ D: & X_{bd} + X_{cd} = X_{de} + X_{df} \\ E: & X_{ce} + X_{de} = X_{ef} \end{array}\)
あとはこれを PuLP でそのままプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 最小費用フロー
import pulp
prob = pulp.LpProblem('min-flow')
# 辺
es = ['ab', 'ac', 'bc', 'bd', 'cd', 'ce', 'de', 'df', 'ef']
# 容量
ws = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# コスト
cs = [3, 7, 1, 2, 9, 1, 7, 8, 4]
# 変数
vs = {e: pulp.LpVariable('x{}'.format(e), lowBound = 0, upBound = m) for e, m in zip(es, ws)}
# 目的関数
prob += pulp.lpDot(cs, [vs[e] for e in es])
# 制約条件
prob += vs['ab'] + vs['ac'] == 6
prob += vs['ab'] == vs['bc'] + vs['bd']
prob += vs['ac'] + vs['bc'] == vs['cd'] + vs['ce']
prob += vs['bd'] + vs['cd'] == vs['de'] + vs['df']
prob += vs['ce'] + vs['de'] == vs['ef']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es:
print(e, vs[e].value())
print("z", prob.objective.value())
Status Optimal ab 5.0 ac 1.0 bc 2.0 bd 3.0 cd 0.0 ce 3.0 de 2.0 df 1.0 ef 5.0 z 75.0
最小費用は 75 になりました。ところで、流すものの総量 f を 1 として最小費用フロー問題を解くと、最短経路 (最小路) を求めることができます。上図の場合は次のようになります。
Status Optimal ab 1.0 ac 0.0 bc 1.0 bd 0.0 cd 0.0 ce 1.0 de 0.0 df 0.0 ef 1.0 z 9.0
最短経路は A -> B -> C -> E -> F で、費用は 9 になりました。
●参考 URL
- 最適化基礎 第11回 最小費用流問題 最大重みマッチングとオークション [PDF], (塩浦昭義さん)
●二部グラフの最大マッチング
頂点を 2 つの集合に分けたとき、同じ集合の頂点間には辺が無く、異なる集合の頂点間にのみ辺があるグラフを「二部グラフ」といいます。そして、頂点を共有していない辺の部分集合を「マッチング」といい、できるだけ大きな部分集合を求めることを「最大マッチング問題」といいます。二部グラフとマッチングの例を下図に示します。
緑の太線は最大マッチングの一例です。マッチングのうち、すべての頂点がいずれかの辺の頂点になっているものを「完全マッチング」といいます。上図は完全マッチングにもなっています。このように、完全マッチングは最大マッチングになります。
最大マッチング問題にも効率的な解法アルゴリズムがいくつか考案されていますが、最大フロー問題に帰着させると線形計画法を使って解くことが可能です。ソースの頂点を s とし、シンクの頂点を t とします。s から集合 S の頂点 {a, b, c, d, e} に辺を引き、集合 T の頂点 {v, w, x, y, z} から t に辺を引きます。各辺の容量を 1 として、頂点 s から頂点 t までの最大フローを求めるとき、S から T に流れる辺が求める「最大マッチング」となります。
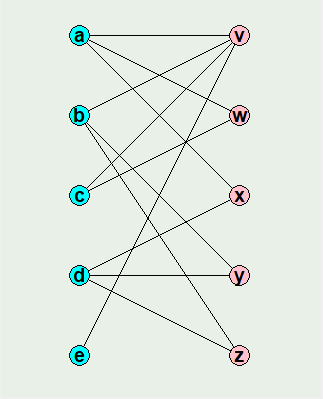
図 : 二部グラフの例 (出典 : 参考文献 1 『データ構造とアルゴリズム』)
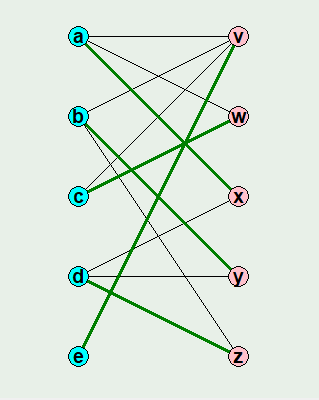図 : マッチングの例
プログラムと実行結果を示します。
リスト : 最大マッチング問題
import pulp
prob = pulp.LpProblem('matching', sense = pulp.LpMaximize)
# 辺
es1 = ['sa', 'sb', 'sc', 'sd', 'se']
es2 = ['av', 'aw', 'ax', 'bv', 'by', 'bz',
'cv', 'cw', 'dx', 'dy', 'dz', 'ev']
es3 = ['vt', 'wt', 'xt', 'yt', 'zt']
# 変数
xs = {e: pulp.LpVariable(e, cat = 'Binary') for e in es1 + es2 + es3}
# 目的関数
prob += pulp.lpSum([xs[e] for e in es1])
# 制約条件
prob += xs['sa'] == xs['av'] + xs['aw'] + xs['ax']
prob += xs['sb'] == xs['bv'] + xs['by'] + xs['bz']
prob += xs['sc'] == xs['cv'] + xs['cw']
prob += xs['sd'] == xs['dx'] + xs['dy'] + xs['dz']
prob += xs['se'] == xs['ev']
prob += xs['vt'] == xs['av'] + xs['bv'] + xs['cv'] + xs['ev']
prob += xs['wt'] == xs['aw'] + xs['cw']
prob += xs['xt'] == xs['ax'] + xs['dx']
prob += xs['yt'] == xs['by'] + xs['dy']
prob += xs['zt'] == xs['bz'] + xs['dz']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es2:
print(e, xs[e].value())
print("z", prob.objective.value())
Status Optimal av 0.0 aw 0.0 ax 1.0 bv 0.0 by 0.0 bz 1.0 cv 0.0 cw 1.0 dx 0.0 dy 1.0 dz 0.0 ev 1.0 z 5.0
辺は a - x, b - z, c - w, d - y, e - v の 5 つで、当然ですが完全マッチングになりました。
●参考文献・URL
- A.V.Aho, John E. Hopcroft, Jeffrey D. Ulman, 『データ構造とアルゴリズム』, 培風館, 1987
- 実世界で超頻出！二部マッチング (輸送問題、ネットワークフロー問題）の解法を総整理！ - Qiita, (Kensuke Otsuki さん)
●二部グラフの最小重み最大マッチング
二部グラフの各辺に重みが定義されていて、その総和が最小となる最大マッチングを求めることを考えます。これは「最小費用フロー問題」に帰着させることにより、線形計画法で解くことが可能です。今回は簡単な例題として、最大マッチングの二部グラフで、辺の重みを下図のように定義したとき、総和が最小となる完全マッチングを求めます。
辺 : a-v a-w a-x b-v b-y b-z c-v c-w d-x d-y d-z e-v ------+------------------------------------------------- 重み : 3 7 1 2 9 1 7 8 4 2 6 5
プログラムは簡単です。最大マッチングと同様に、ソースの頂点 s とシンクの頂点 t を用意して、各頂点と辺を結びます。各辺の容量を 1 として総量 5 をソースからシンクに流すとき、重みが最小となる流し方が「最小重み完全マッチング」になります。
プログラムと実行結果を示します。
リスト : 最小重み完全マッチング
import pulp
prob = pulp.LpProblem('matching')
# 辺
es1 = ['sa', 'sb', 'sc', 'sd', 'se']
es2 = ['av', 'aw', 'ax', 'bv', 'by', 'bz',
'cv', 'cw', 'dx', 'dy', 'dz', 'ev']
es3 = ['vt', 'wt', 'xt', 'yt', 'zt']
# 重み (es2 に対応)
ws = [3, 7, 1, 2, 9, 1, 7, 8, 4 , 2, 6, 5]
# 変数
xs = {e: pulp.LpVariable(e, cat = 'Binary') for e in es1 + es2 + es3}
# 目的関数
prob += pulp.lpDot(ws, [xs[e] for e in es2])
# 制約条件
prob += pulp.lpSum([xs[e] for e in es1]) == 5
prob += xs['sa'] == xs['av'] + xs['aw'] + xs['ax']
prob += xs['sb'] == xs['bv'] + xs['by'] + xs['bz']
prob += xs['sc'] == xs['cv'] + xs['cw']
prob += xs['sd'] == xs['dx'] + xs['dy'] + xs['dz']
prob += xs['se'] == xs['ev']
prob += xs['vt'] == xs['av'] + xs['bv'] + xs['cv'] + xs['ev']
prob += xs['wt'] == xs['aw'] + xs['cw']
prob += xs['xt'] == xs['ax'] + xs['dx']
prob += xs['yt'] == xs['by'] + xs['dy']
prob += xs['zt'] == xs['bz'] + xs['dz']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es2:
print(e, xs[e].value())
print("z", prob.objective.value())
Status Optimal av 0.0 aw 0.0 ax 1.0 bv 0.0 by 0.0 bz 1.0 cv 0.0 cw 1.0 dx 0.0 dy 1.0 dz 0.0 ev 1.0 z 17.0
重みの最小値は 17 になりました。たまたま最大マッチングで求めたマッチングと一致しました。興味のある方はデータを変えて試してみてください。
●割当て問題
n 人の作業員に n 個の仕事を割り当てるとき、最も効率の良い割り当て方 (または利益が最大となる割り当て方) を見つけることを「割当て問題」といいます。この問題は「ハンガリー法」という解法アルゴリズムが考案されていますが、線形計画法でも解くことが可能です。今回は簡単な例題として、各作業員の作業とその費用が下表 (出典 : 参考 URL 1『割当問題』) に示されているとき、総費用が最小となる割り当て方を求めてみましょう。
表 : 作業員の費用
作 業
: a b c d e
---+----------------
A : 9 5 1 9 7
作 B : 2 8 2 7 5
業 C : 1 3 9 5 9
員 D : 8 7 2 6 4
E : 2 3 6 2 8
割当て問題は、各作業員に異なる仕事を一つずつ割り当てます。作業員 i に作業 j を割り当てるか否かを変数 \(X_{ij}\) で表すことにします。\(X_{ij}\) が 1 ならば作業を行う、0 ならば作業を行いません。作業員 i が作業 j を行う費用を \(W_{ij}\) とすると、目的関数は次のようになります。
\( z = \displaystyle \sum_i \sum_j W_{ij} X_{ij} \)
制約条件も簡単です。各作業員には異なる作業が割り当てられ、各作業には異なる作業員が割り当てられるので、条件は次式のようになります。
1. 作業員 i が行う作業は 1 つ
\( \displaystyle \sum_j X_{ij} = 1, \quad (i = 0, \ldots, n - 1) \)
2. 作業 j に割り当てられる作業員は一人
\( \displaystyle \sum_i X_{ij} = 1, \quad (j = 0, \ldots, n - 1) \)
あとは、これをそのまま PuLP でプログラムするだけです。プログラムと実行結果を示します。
リスト : 割当て問題
import pulp
#
# 作業員の費用
# a b c d e
ps = [[9, 5, 1, 9, 7], # A
[2, 8, 2, 7, 5], # B
[1, 3, 9, 5, 9], # C
[8, 7, 2, 6, 4], # D
[2, 3, 6, 2, 8]] # E
def solver(ws):
prob = pulp.LpProblem('assignment')
# 変数
xs = []
for i in range(len(ws)):
xs1 = [pulp.LpVariable('x_{}_{}'.format(i, j), cat='Binary') for j in range(len(ws))]
xs.append(xs1)
# 目的関数
prob += pulp.lpSum([pulp.lpDot(ws[i], xs[i]) for i in range(len(ws))])
# 制約
for i in range(len(ws)):
prob += pulp.lpSum(xs[i]) == 1 # 作業員に 1 つの仕事
prob += pulp.lpSum([xs[j][i] for j in range(len(ws))]) == 1 # 仕事には一人の作業員
#
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for xs1 in xs:
print([x.value() for x in xs1])
print(prob.objective.value())
# 実行
solver(ps)
Status Optimal [0.0, 0.0, 1.0, 0.0, 0.0] [1.0, 0.0, 0.0, 0.0, 0.0] [0.0, 1.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0, 1.0] [0.0, 0.0, 0.0, 1.0, 0.0] 12.0
割当ては (A, c), (B, a), (C, b), (D, e), (E, d) で、総費用は 12 になりました。ところで、割当て問題は作業員の集合と作業の集合の二部グラフと考えることができるので、「最小重み最大マッチング」と同じ方法で解くことができます。ご参考までに、プログラムと実行結果を示します。
リスト : 割当て問題 (最小重み最大マッチング)
def solver1(ws):
prob = pulp.LpProblem('assignment')
# 変数
xs = []
for i in range(len(ws)):
xs1 = [pulp.LpVariable('x_{}_{}'.format(i, j), cat='Binary') for j in range(len(ws))]
xs.append(xs1)
# ソースから作業員への辺
ys = [pulp.LpVariable('y_{}'.format(j), cat='Binary') for j in range(len(ws))]
# 仕事からシンクへの辺
zs = [pulp.LpVariable('z_{}'.format(j), cat='Binary') for j in range(len(ws))]
# 目的関数
prob += pulp.lpSum([pulp.lpDot(ws[i], xs[i]) for i in range(len(ws))])
# 制約
prob += pulp.lpSum(ys) == len(ws) # 流す総量
for i in range(len(ws)):
prob += ys[i] == pulp.lpSum(xs[i])
prob += pulp.lpSum([xs[j][i] for j in range(len(ws))]) == zs[i]
#
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for xs1 in xs:
print([x.value() for x in xs1])
print(prob.objective.value())
solver1(ps)
Status Optimal [0.0, 0.0, 1.0, 0.0, 0.0] [1.0, 0.0, 0.0, 0.0, 0.0] [0.0, 1.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0, 1.0] [0.0, 0.0, 0.0, 1.0, 0.0] 12.0
実行結果は同じです。
●参考 URL
- 割当問題, (木暮仁さん)
●多品種フロー問題
「最大フロー問題」はネットワーク上でソース s からシンク t まで流すことができる「もの」の最大値を求める問題でした。ソースとシンクのペアは (s, t) の一つだけですが、これを複数に増やしたものが「多品種フロー問題」です。品種はソースとシンクのペア (si, ti) のことと考えてください。ネットワーク上に複数の「もの」が流れるので、制約条件は次のようになります。
- 各辺には容量があり、そこを流れる各品種の量の総和がそれを超えてはならない
- ソースとシンク以外の頂点において、各品種ごとに流入する総量と流出する総量は等しい (保存則)
今回は簡単な例題として、下図に示す有効グラフにおいて、(A, E) と (B, F) の二品種の最大フローを求めてみましょう。
辺 : 容量
-------+------
Ｂ─────Ｄ A -> B : 5
／│ ／│＼ A -> C : 2
／ │ ／ │ ＼ B -> C : 6
Ａ │ ／ │ Ｆ B -> D : 4
＼ │ ／ │ ／ C -> D : 2
＼│／ │／ C -> E : 3
Ｃ─────Ｅ D -> E : 3
D -> F : 1
E -> F : 9
図 : 有向グラフ
(A, E) の品種を X, (B, F) の品種を Y とします。辺 i -> j に対応する変数を \(X_{ij}, Y_{ij}\) とすると、目的関数と制約条件は次式のようになります。
\( f = X_{ab} + X_{ac} + Y_{bc} + Y_{bd} \)
1. 辺の容量
\(\begin{array}{l} 0 \leq X_{ab} + Y_{ab} \leq 5 \\ 0 \leq X_{ac} + Y_{ac} \leq 2 \\ 0 \leq X_{bc} + Y_{bc} \leq 6 \\ 0 \leq X_{bd} + Y_{bd} \leq 4 \\ 0 \leq X_{cd} + Y_{cd} \leq 2 \\ 0 \leq X_{ce} + Y_{ce} \leq 3 \\ 0 \leq X_{de} + Y_{de} \leq 3 \\ 0 \leq X_{df} + Y_{df} \leq 1 \\ 0 \leq X_{ef} + Y_{ef} \leq 9 \end{array}\)
2. 各頂点の保存則
\(X\)
\(\begin{array}{l} B: X_{ab} = X_{bd} + X_{bc} \\ C: X_{ac} + X_{bc} = X_{cd} + X_{ce} \\ D: X_{bd} + X_{cd} = X_{de} + X_{df} \\ E: X_{ce} + X_{de} = X_{ab} + X_{ac} \\ \end{array}\)
\(Y\)
\(\begin{array}{l} C: Y_{ac} + Y_{bc} = Y_{cd} + Y_{ce} \\ D: Y_{bd} + Y_{cd} = Y_{de} + Y_{df} \\ E: Y_{ce} + Y_{de} = Y_{ef} \\ F: Y_{df} + Y_{ef} = Y_{bc} + Y_{bd} \end{array}\)
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 多品種フロー問題
import pulp
prob = pulp.LpProblem('max-flow', sense = pulp.LpMaximize)
# 辺
es = ['ab', 'ac', 'bc', 'bd', 'cd', 'ce', 'de', 'df', 'ef']
# 最大容量
ms = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# 変数
xs = {e: pulp.LpVariable('x{}'.format(e), lowBound = 0) for e in es}
ys = {e: pulp.LpVariable('y{}'.format(e), lowBound = 0) for e in es}
# 目的関数
prob += xs['ab'] + xs['ac'] + ys['bc'] + ys['bd']
# 制約条件
for e, m in zip(es, ms):
prob += xs[e] + ys[e] <= m
prob += xs['ab'] == xs['bc'] + xs['bd']
prob += xs['ac'] + xs['bc'] == xs['cd'] + xs['ce']
prob += xs['bd'] + xs['cd'] == xs['de'] + xs['df']
prob += xs['ce'] + xs['de'] == xs['ab'] + xs['ac']
prob += ys['ac'] + ys['bc'] == ys['cd'] + ys['ce']
prob += ys['bd'] + ys['cd'] == ys['de'] + ys['df']
prob += ys['ce'] + ys['de'] == ys['ef']
prob += ys['df'] + ys['ef'] == ys['bc'] + ys['bd']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es:
print(e, 'x =', xs[e].value(), 'y =', ys[e].value())
print("f", prob.objective.value())
Status Optimal ab x = 3.0 y = 0.0 ac x = 2.0 y = 0.0 bc x = 0.0 y = 1.0 bd x = 3.0 y = 1.0 cd x = 0.0 y = 0.0 ce x = 2.0 y = 1.0 de x = 3.0 y = 0.0 df x = 0.0 y = 1.0 ef x = 0.0 y = 1.0 f 7.0
最大フローは 7 になりました。今回は X を 5 個と Y を 2 個流す解が求まりましたが、解はこれひとつだけではありません。たとえば、制約条件に prob += ys['bc'] + ys['bd'] >= 3 を追加すれば、Y を 3 個以上流す解を (それが存在すれば) 求めることができます。
●多品種で最小費用フローを求める
次は、多品種の「最小費用フロー問題」を解いてみましょう。上図と同じ経路図において、品種 X と品種 Y の費用が以下のように定義されているとします。
辺 : ab ac bc bd cd ce de df ef ---+---------------------------- X : 3 7 1 2 9 1 7 8 4 Y : 5 9 3 4 11 3 9 10 6
X の費用を \(Wx_{ij}\), Y の費用を \(Wy_{ij}\) とすると、目的関数は次のようになります。
\( z = \displaystyle \sum_{i,j} Wx_{ij} X_{ij} + \sum_{i,j} Wy_{ij} Y_{ij} \)
今回は X を 4 個, Y を 2 個流すことにします。プログラムリストと実行結果を示します。
リスト : 多品種の最小費用フロー問題
import pulp
prob = pulp.LpProblem('min-flow')
# 辺
es = ['ab', 'ac', 'bc', 'bd', 'cd', 'ce', 'de', 'df', 'ef']
# 最大容量
ms = [5, 2, 6, 4, 2, 3, 3, 1, 9]
# コスト
wxs = [3, 7, 1, 2, 9, 1, 7, 8, 4]
wys = [5, 9, 3, 4, 11, 3, 9, 10, 6]
# 変数
xs = {e: pulp.LpVariable('x{}'.format(e), lowBound = 0) for e in es}
ys = {e: pulp.LpVariable('y{}'.format(e), lowBound = 0) for e in es}
# 目的関数
prob += pulp.lpDot(wxs, [xs[e] for e in es]) + pulp.lpDot(wys, [ys[e] for e in es])
# 制約条件
for e, m in zip(es, ms):
prob += xs[e] + ys[e] <= m
prob += xs['ab'] + xs['ac'] == 4
prob += xs['ab'] == xs['bc'] + xs['bd']
prob += xs['ac'] + xs['bc'] == xs['cd'] + xs['ce']
prob += xs['bd'] + xs['cd'] == xs['de'] + xs['df']
prob += xs['ce'] + xs['de'] == xs['ab'] + xs['ac']
prob += ys['bc'] + ys['bd'] == 2
prob += ys['ac'] + ys['bc'] == ys['cd'] + ys['ce']
prob += ys['bd'] + ys['cd'] == ys['de'] + ys['df']
prob += ys['ce'] + ys['de'] == ys['ef']
prob += ys['df'] + ys['ef'] == ys['bc'] + ys['bd']
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for e in es:
print(e, 'x =', xs[e].value(), 'y =', ys[e].value())
print("z", prob.objective.value())
Status Optimal ab x = 4.0 y = 0.0 ac x = 0.0 y = 0.0 bc x = 3.0 y = 0.0 bd x = 1.0 y = 2.0 cd x = 0.0 y = 0.0 ce x = 3.0 y = 0.0 de x = 1.0 y = 1.0 df x = 0.0 y = 1.0 ef x = 0.0 y = 1.0 z 60.0
最小費用は 60 になりました。ちなみに、X を 3 個、Y を 3 個流すことにすると、最小費用は 67 になります。興味のある方はいろいろ試してみてください。
●参考 URL
- ネットワークフローとその代表的な問題 [PDF], (金子紘也さん)