●施設配置問題
「施設配置問題 (facility location problem)」は、工場や倉庫など重要な施設の配置を決定する問題です。施設配置問題には様々な種類の問題がありますが、今回は基本的な問題である p-median 問題と p-center 問題を取り上げます。どちらの問題も、施設の候補地の集合と、その利用者の集合が与えられていて、ある基準を満たすよう候補地の集合から p 個の施設を選択します。p-median 問題は、利用者の移動距離の総和が最小となる配置を求めます。p-center 問題は、利用者の最大の移動距離が最小となる配置を求めます。
●p-median 問題
簡単な例題として、施設の候補地の集合 F = {f0, f1, f2} と利用者の集合 D = {d0, d1, d2} において、施設 f を 2 つ選ぶ場合を考えてみましょう。下表に施設と利用者の距離と利用者の人数を示します。
表 : 人数と距離
: f0 : f1 : f2
--------+----+----+-----
d0 (2) : 11 : 3 : 6
d1 (10) : 1 : 7 : 9
d2 (4) : 8 : 5 : 12
出典 : ロジスティクス工学 05 施設配置 (参考 URL 2)
施設 \(f_{i}\) の選択を表す変数 (Binary) を \(F_{i}\) とし、利用者 \(d_{i}\) が施設 \(f_{j}\) を使うことを表す変数 (Binary) を \(X_{ij}\) とします。\(d_{i}\) の人数を \(W_{i}, d_{i}\) と \(f_{j}\) の距離を \(C_{ij}\) とすると、目的関数と制約条件は次のようになります。
\( \displaystyle \sum_i \sum_j W_{i} C_{ij} X_{ij} \)
1. 配置する施設は二つ
\( \displaystyle \sum_i F_{i} = 2 \)
2. 利用者が使用する施設は一つだけ
\( \displaystyle \sum_j X_{ij} = 1, \quad (i = 0, 1, 2) \)
3. \(F_{j}\) が 0 ならば \(X_{ij}\) も 0 になる
\( X_{ij} \leq F_{j}, \quad (i = 0, 1, 2, j = 0, 1, 2) \)
最後の制約条件は、施設 \(F_{j}\) を配置しないのであれば、その施設は利用できないことをことを表します。あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 施設配置問題 (p-median)
import pulp
prob = pulp.LpProblem('p-median')
# コスト (距離)
# f0 f1 f2
cs = [[11, 3, 6], # d0
[ 1, 7, 9], # d1
[ 8, 5, 12]] # d2
# 人数
ws = [2, 10, 4]
# 変数
# fs[i] : 施設 fi を配置するか否か
# xs[i][j] : di が fi を利用するか否か
#
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(3)]
xs = []
for i in range(3):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(3)]
xs.append(xs1)
# 目的関数
prob += pulp.lpSum([ws[i] * pulp.lpDot(cs[i], xs[i]) for i in range(3)])
# 制約条件
prob += pulp.lpSum(fs) == 2
for i in range(3):
prob += pulp.lpSum(xs[i]) == 1
for i in range(3):
for j in range(3):
prob += xs[i][j] <= fs[j]
#
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([f.value() for f in fs])
for xs1 in xs:
print([x.value() for x in xs1])
print(prob.objective.value())
Status Optimal [1.0, 1.0, 0.0] [0.0, 1.0, 0.0] [1.0, 0.0, 0.0] [0.0, 1.0, 0.0] 36.0
施設を配置するのは f0 と f1 で、d0 と d2 が f1 を利用し、d1 が f0 を利用します。このときの費用は 36 になりました。
次は、顧客 (1 つ) を平面上にランダムに n 個配置して、その中から施設となるものを p 個選んでみましょう。この場合、施設と顧客の距離の総和が最小となる p 個のグループに顧客を分けることになります。プログラムは次のようになります。
リスト : p-median 問題 (乱数での配置)
def solver(ps, p):
size = len(ps)
cs = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('p-median')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum([pulp.lpDot(c, x) for c, x in zip(cs, xs)])
# 制約条件
prob += pulp.lpSum(fs) == p
for x in xs:
prob += pulp.lpSum(x) == 1
for i in range(size):
prob += xs[i][i] >= fs[i] # 削除しても動作する
for j in range(size):
prob += xs[i][j] <= fs[j]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, xs)
# 実行
for n in [60, 80, 100, 120, 140]:
print("-----", n, "-----")
solver(make_data(n), n // 20)
関数 make_matirx() や draw() は拙作のページ「巡回セールスマン問題」のプログラムを流用しています。制約条件では、次の制約式を追加しています。
施設 \(F_{i}\) を選んだ場合、i 番目の顧客は自分自身を利用することになるので、\(X_{ii}\) の値は 1 になります。上記の制約条件を追加することで、fs[i] が 1 ならば xs[i][i] の値を 1 にすることができます。なお、この制約条件がなくてもプログラムは正常に動作しますが、制約を追加すると実行時間がほんのちょっとですが速くなるようです。
施設の個数は顧客数の 1 / 20 としました。あとのプログラムは簡単なので、説明は割愛いたします。プログラムの実行例を示します。
----- 60 ----- Status Optimal z 6248.465323403335 0.9079859256744385
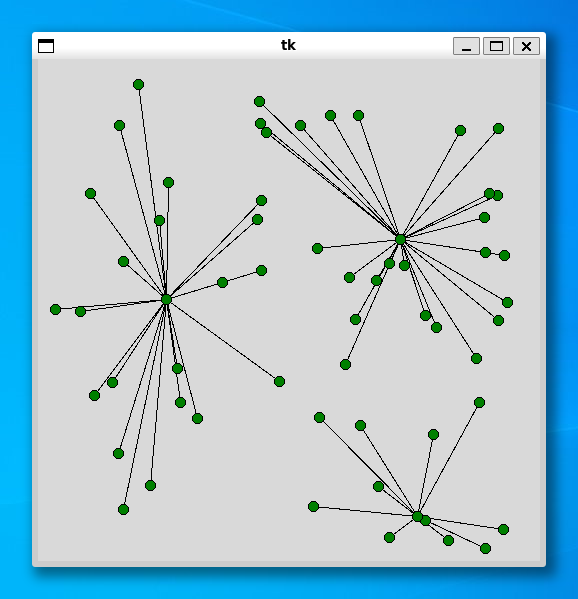
----- 80 ----- Status Optimal z 6770.522178037366 0.7746577262878418
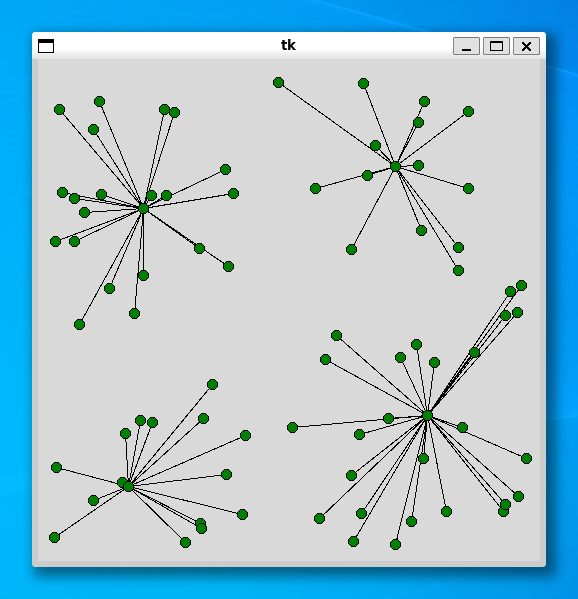
----- 100 ----- Status Optimal z 7413.4740469953595 1.1458191871643066
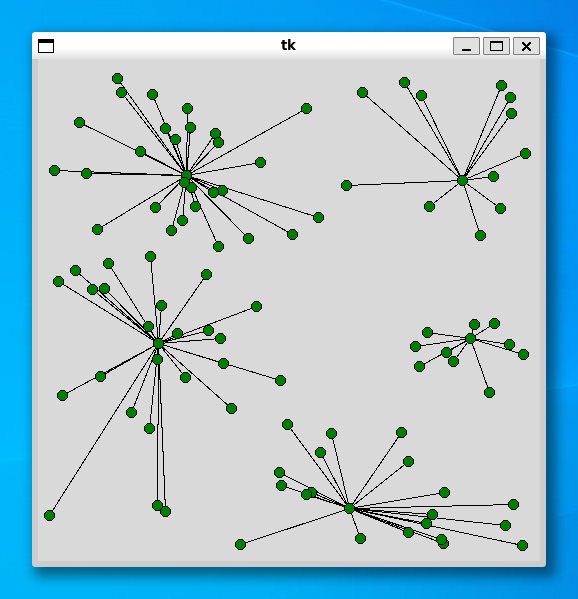
----- 120 ----- Status Optimal z 8525.763664093749 4.902146577835083
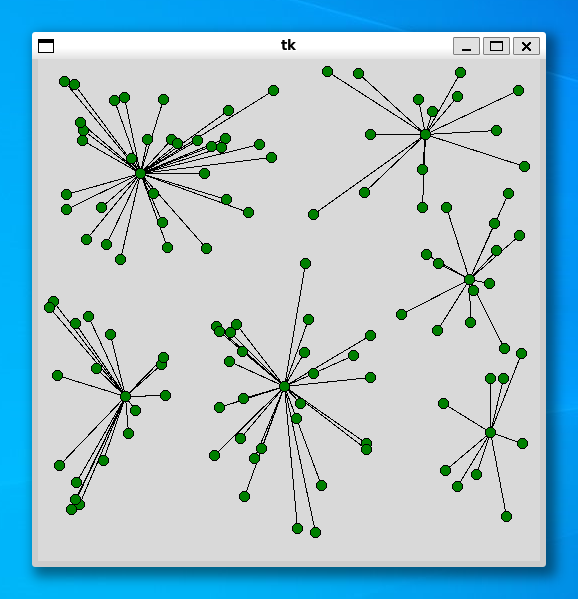
----- 140 ----- Status Optimal z 9315.709622085995 3.148613452911377
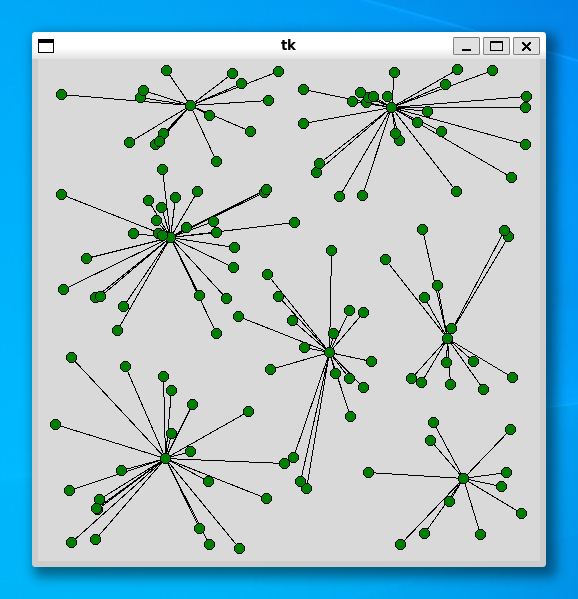
- 実行環境 : Python 3.10.6, PuLP 2.7.0, Ubunts 22.04 LTS (WSL2, Windows 10), Intel Core i5-6200U 2.30GHz
顧客の個数が 100 程度であれば、制約式を強化しなくても高速に解くことができるようです。ところで、施設の個数の割合を変更すると、実行時間が変化するかもしれません。興味のある方はいろいろ試してみてください。
●p-center 問題
次は p-center 問題のプログラムを作りましょう。まずは最初に p-median と同じ例題を取り上げます。p-center 問題の場合、利用者の人数は関係なく、施設と利用者の距離が問題になります。
表 : 距離
: f0 : f1 : f2
---+----+----+-----
d0 : 11 : 3 : 6
d1 : 1 : 7 : 9
d2 : 8 : 5 : 12
出典 : 参考 URL 2『ロジスティクス工学 05 施設配置』
施設 \(f_{i}\) の選択を表す変数 (Binary) を \(F_{i}\) とし、利用者 \(d_{i}\) が施設 \(f_{j}\) を使うことを表す変数 (Binary) を \(X_{ij}\) とします。\(d_{i}\) と \(f_{j}\) の距離を \(C_{ij}\) とすると、目的関数と制約条件は次のようになります。
1. i と j の距離を z 以下にする
\( \displaystyle \sum_j C_{ij} X_{ij} \leq z \)
2. 配置する施設は二つ
\( \displaystyle \sum_i F_{i} = 2 \)
3. 利用者が使用する施設は一つだけ
\( \displaystyle \sum_j X_{ij} = 1, \quad (i = 0, 1, 2) \)
4. \(F_{j}\) が 0 ならば \(X_{ij}\) も 0 になる
\( X_{ij} \leq F_{j}, \quad (i = 0, 1, 2, j = 0, 1, 2) \)
ポイントは最大の移動距離を変数 z で表すところです。変数 z を目的関数にすることで、z を最小化することができます。そして、制約条件に最初の式を追加します。i -> j までの距離が z 以下である条件を追加することで、z が最小となるように \(X_{ij}\) が選択されます。
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 施設配置問題 (p-center)
import pulp
prob = pulp.LpProblem('p-center')
# コスト (距離)
# f0 f1 f2
cs = [[11, 3, 6], # d0
[ 1, 7, 9], # d1
[ 8, 5, 12]] # d2
# 変数
# fs[i] : 施設 fi を配置するか否か
# xs[i][j] : di が fi を利用するか否か
#
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(3)]
xs = []
for i in range(3):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(3)]
xs.append(xs1)
z = pulp.LpVariable('z', lowBound = 0)
# 目的関数
prob += z
# 制約条件
prob += pulp.lpSum(fs) == 2
for c, x in zip(cs, xs):
prob += pulp.lpDot(c, x) <= z
for i in range(3):
prob += pulp.lpSum(xs[i]) == 1
for i in range(3):
for j in range(3):
prob += xs[i][j] <= fs[j]
#
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([f.value() for f in fs])
for xs1 in xs:
print([x.value() for x in xs1])
print(prob.objective.value())
Status Optimal [1.0, 1.0, 0.0] [0.0, 1.0, 0.0] [1.0, 0.0, 0.0] [0.0, 1.0, 0.0] 5.0
施設を配置するのは f0 と f1 で、d0 と d2 が f1 を利用し、d1 が f0 を利用します。このときの最大距離 z は d2 -> f1 の 5 になりました。d0 -> f1 は 3 で、d1 -> f0 は 1 なので、z よりも小さく条件を満たしていることがわかります。
次は、顧客 (1 つ) を平面上にランダムに n 個配置して、その中から施設となるものを p 個選んでみましょう。この場合、施設と顧客の最大距離が最小となる p 個のグループに顧客を分けることになります。プログラムは次のようになります。
リスト : p-center 問題 (乱数での配置)
def solver(ps, p):
size = len(ps)
cs = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('p-center')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
z = pulp.LpVariable('z', lowBound = 0)
# 目的関数
prob += z
# 制約条件
prob += pulp.lpSum(fs) == p
for c, x in zip(cs, xs):
prob += pulp.lpDot(c, x) <= z
for x in xs:
prob += pulp.lpSum(x) == 1
for i in range(size):
prob += xs[i][i] >= fs[i] # この条件がないと p-center は動作しない
for j in range(size):
prob += xs[i][j] <= fs[j]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, xs)
# 実行
for n in [20, 40, 60, 80, 100]:
print("-----", n, "-----")
solver(make_data(n), n // 10)
p-median の場合、制約条件 xs[i][i] >= fs[i] はなくても動作しましたが、p-center では必要になります。省略すると正常に動作しません。ご注意くださいませ。
施設の個数は顧客数の 1 / 10 としました。あとのプログラムは簡単なので、説明は割愛いたします。プログラムの実行例を示します。
----- 20 ----- Status Optimal z 233.829 0.18664097785949707
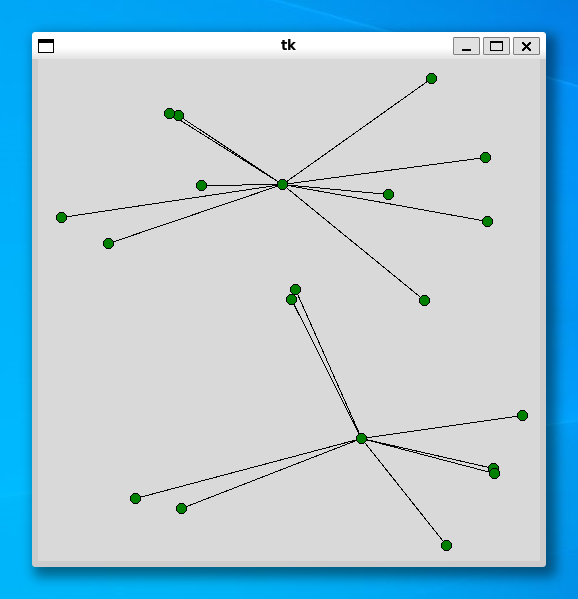
----- 40 ----- Status Optimal z 158.04113 1.6332387924194336
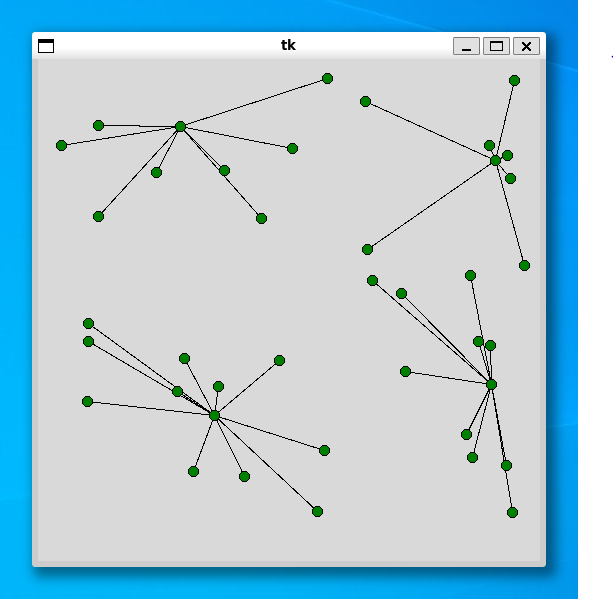
----- 60 ----- Status Optimal z 126.81088 4.916394233703613
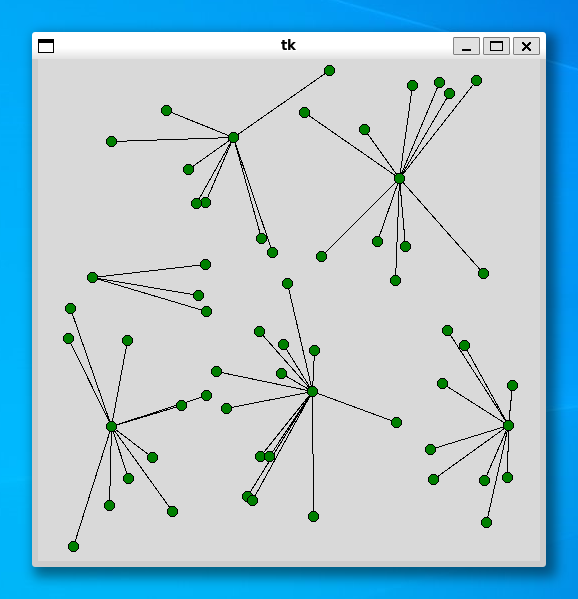
----- 80 ----- Status Optimal z 111.12605 11.52083158493042
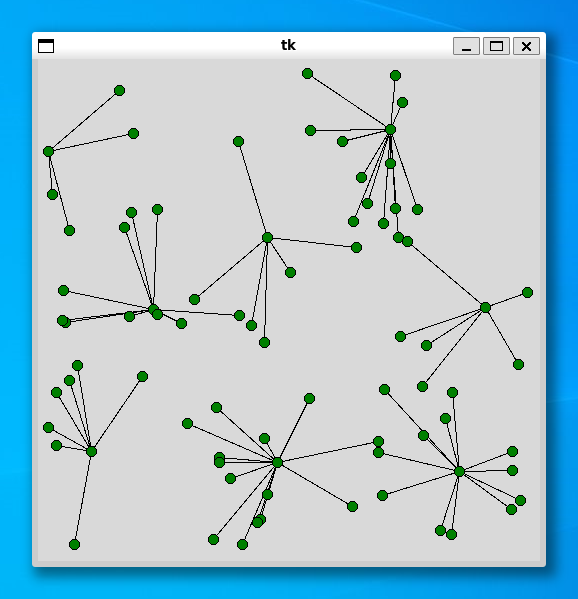
----- 100 ----- Status Optimal z 100.0 25.18533682823181
- 実行環境 : Python 3.10.6, PuLP 2.7.0, Ubunts 22.04 LTS (WSL2, Windows 10), Intel Core i5-6200U 2.30GHz
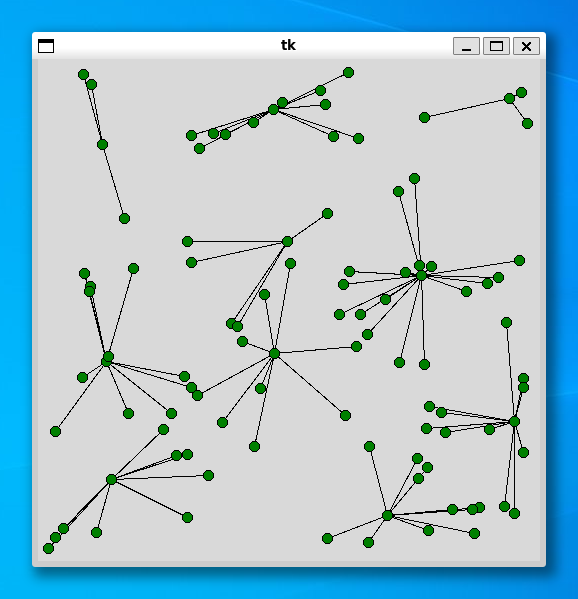
ご参考までに、同じデータ (顧客 100, 施設 10) を使って、p-median 問題と p-center 問題を解いた結果を示します。
>>> import shisetu >>> xs = shisetu.make_data(100) >>> shisetu.solver_median(xs, 10) Status Optimal z 4971.496149734859 2.376474618911743 >>> shisetu.solver_center(xs, 10) Status Optimal z 90.934042 16.181299209594727
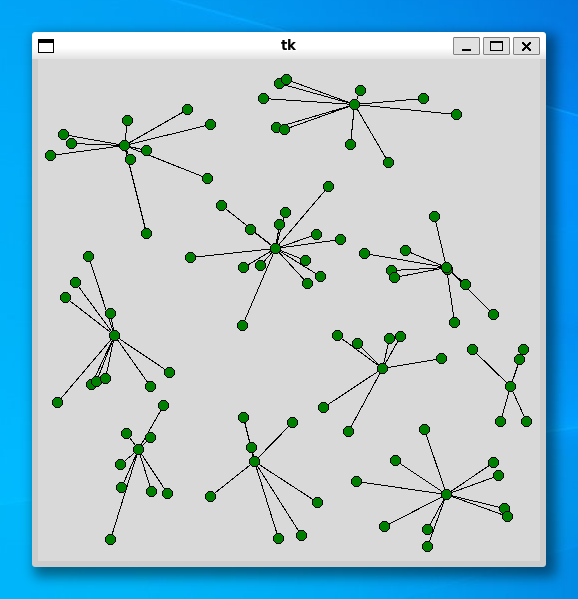
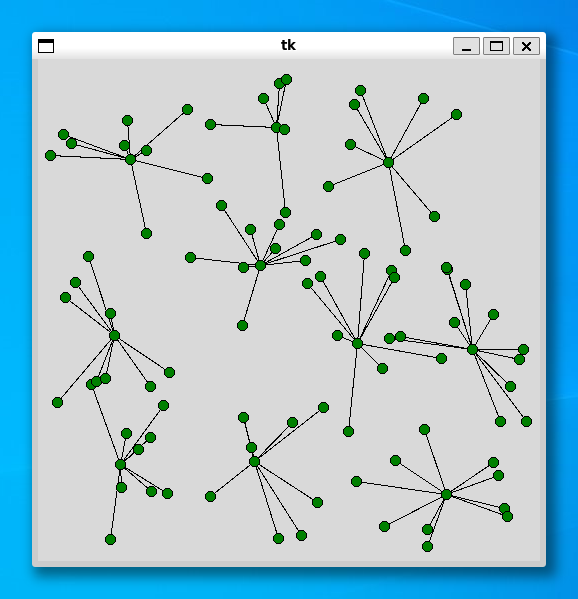
p-center 問題は p-median 問題よりも実行時間がかかるようです。それでも、顧客が 100 個程度であれば 1 分もかからずに解くことができました。興味のある方はいろいろ試してみてください。
●参考 URL
- 数理最適化入門(4):施設配置の数理モデル [PDF], (田中健一さん)
- ロジスティクス工学 05 施設配置 [PDF], (宮本裕一郎さん)
●プログラムリスト
#
# shisetu.py : 施設配置問題 (p-median と p-center)
#
# Copyright (C) 2019-2023 Makoto Hiroi
#
import sys, math, time, random
import pulp
import tkinter as tk
# 乱数でデータを生成
def make_data(n):
return [(random.randrange(480) + 10, random.randrange(480) + 10) for _ in range(n)]
# 描画
def draw(ps, xs):
root = tk.Tk()
c0 = tk.Canvas(root, width = 500, height = 500)
c0.pack()
for i in range(len(xs)):
for j in range(len(xs)):
if xs[i][j].value() == 0: continue
c0.create_line(ps[i][0], ps[i][1], ps[j][0], ps[j][1], width = 1.0)
for i, j in ps:
c0.create_oval(i - 5, j - 5, i + 5, j + 5, fill = 'green')
root.mainloop()
# 標準入力よりデータを読み込む
def read_data():
buff = []
for a in sys.stdin:
b = a.split()
buff.append((int(b[0]), int(b[1])))
return buff
# 距離を求める
def distance(p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx * dx + dy * dy)
# 隣接行列の生成
def make_matrix(ps):
return [[distance(p1, p2) for p2 in ps] for p1 in ps]
# 解を求める
def solver_median(ps, p):
size = len(ps)
cs = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('p-median')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum([pulp.lpDot(c, x) for c, x in zip(cs, xs)])
# 制約条件
prob += pulp.lpSum(fs) == p
for x in xs:
prob += pulp.lpSum(x) == 1
for i in range(size):
prob += xs[i][i] >= fs[i]
for j in range(size):
prob += xs[i][j] <= fs[j]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, xs)
def solver_center(ps, p):
size = len(ps)
cs = make_matrix(ps) # 隣接行列
prob = pulp.LpProblem('p-center')
# 変数の生成
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat='Binary') for j in range(size)]
xs.append(xs1)
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
z = pulp.LpVariable('z', lowBound = 0)
# 目的関数
prob += z
# 制約条件
prob += pulp.lpSum(fs) == p
for c, x in zip(cs, xs):
prob += pulp.lpDot(c, x) <= z
for x in xs:
prob += pulp.lpSum(x) == 1
for i in range(size):
prob += xs[i][i] >= fs[i]
for j in range(size):
prob += xs[i][j] <= fs[j]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, xs)
●施設配置問題 (2)
施設配置問題の続きです。今回は集合被覆問題と最大被覆問題を取り上げます。
●集合被覆問題
施設配置問題でいう「集合被覆問題 (set cover problem)」は、施設の候補地の集合 F と利用者の集合 D が与えられたとき、すべての利用者が施設を利用でき、なおかつ施設の個数を最小にする配置を求める問題です。数学での定義は参考 URL 3『集合被覆問題 - Wikipedia』をお読みください。
簡単な例題として、利用者 \(D_{i}\) が利用できる施設の候補地 \(F_{j}\) が下表のように与えられているとき、施設の個数が最小となる配置を求めてみましょう。
表 : 利用可能な施設
: f0 : f1 : f2 : f3 : f4
----+----+----+----+----+----
d0 : 1 : 0 : 0 : 0 : 1
d1 : 1 : 1 : 0 : 0 : 0
d2 : 0 : 1 : 1 : 0 : 0
d3 : 0 : 0 : 1 : 1 : 0
d4 : 0 : 0 : 0 : 1 : 1
(出典 : 参考 URL 2 『ロジスティクス工学 05 施設配置』)
施設 \(f_{j}\) の選択を表す変数 (Binary) を \(F_{j}\) とし、上表の要素を \(W_{ij}\) で表すことにします。目的関数と制約条件は次のようになります。
\( \displaystyle \sum_j F_{j} \)
\( \displaystyle \sum_j W_{ij} F_{j} \geq 1 \quad (i= 0, 1, 2, 3, 4) \)
目的関数は簡単ですね。制約条件ですが、利用者 \(D_{i}\) が利用できる施設は W の i 行目に定義されているので、その要素と F の要素の内積を計算して、その値が 1 以上であれば \(D_{i}\) は施設を利用することができます。
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 集合被覆問題 (set cover problem)
import pulp
prob = pulp.LpProblem('set-cover')
# 利用可能な施設
# f0 f1 f2 f3 f4
ws = [[ 1, 0, 0, 0, 1], # d0
[ 1, 1, 0, 0, 0], # d1
[ 0, 1, 1, 0, 0], # d2
[ 0, 0, 1, 1, 0], # d3
[ 0, 0, 0, 1, 1]] # d4
# 変数
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(5)]
# 目的関数
prob += pulp.lpSum(fs)
# 制約条件
for w in ws:
prob += pulp.lpDot(w, fs) >= 1
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([f.value() for f in fs])
print(prob.objective.value())
Status Optimal [0.0, 1.0, 0.0, 1.0, 1.0] 3.0
配置する施設は f1, f3, f4 の三つになりました。
次は、利用者を平面上にランダムに n 個配置し、半径 r 内にある施設を利用できる条件で、集合被覆問題を解いてみましょう。施設は利用者の中から選びます。プログラムは次のようになります。
リスト : 集合被覆問題 (乱数による配置)
# 行列の生成
def make_matrix(ps, r):
def check(l):
if l <= r:
return 1
else:
return 0
return [[check(distance(p1, p2)) for p2 in ps] for p1 in ps]
# 解を求める
def solver_set(ps, r):
size = len(ps)
cs = make_matrix(ps, r)
prob = pulp.LpProblem('set-cover')
# 変数の生成
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum(fs)
# 制約条件
for c in cs:
prob += pulp.lpDot(c, fs) >= 1
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, fs, r)
# 実行
for n in [25, 50, 75, 100]:
print("-----", n, "-----")
solver_set(make_data(n), 100)
関数 make_matrix() は利用者 p1 と施設 p2 の距離を計算して、それが半径 r 以下であれば要素を 1 に、そうでなければ要素を 0 にします。これで利用者が利用できる施設を行列で表すことができます。
それでは実行してみましょう。半径は 100 としました。
----- 25 ----- Status Optimal z 9.0 0.008144140243530273
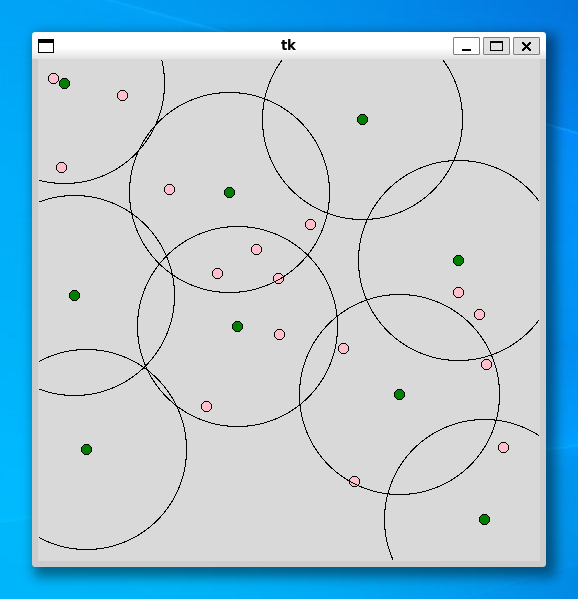
----- 50 ----- Status Optimal z 8.0 0.010876893997192383
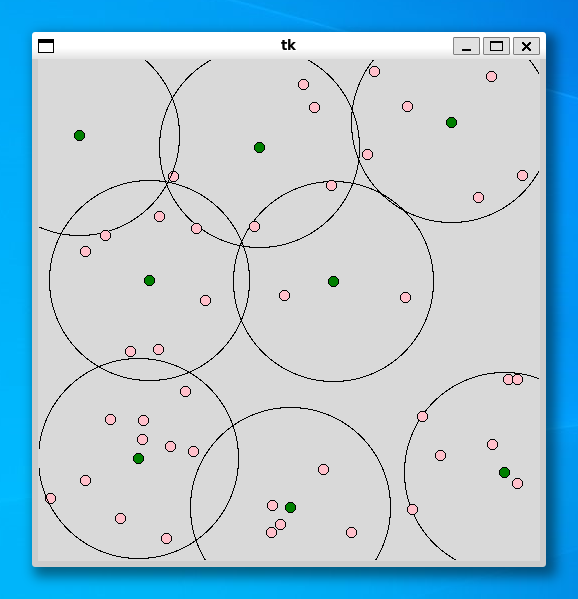
----- 75 ----- Status Optimal z 9.0 0.012598037719726562
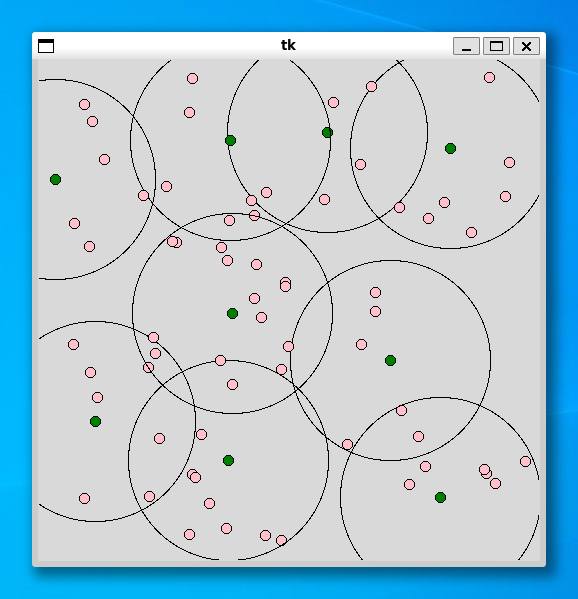
----- 100 ----- Status Optimal z 9.0 0.016979217529296875
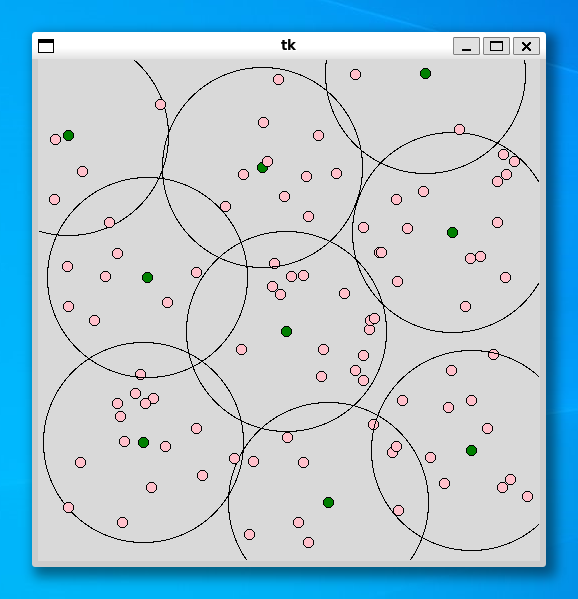
どの利用者 (pink) も施設 (green) を中心とした円の中に入っていることがわかります。実行時間も高速で、利用者の個数が 100 個でもすぐに解を求めることができました。もっと時間がかかると思っていたので、こんなに速いとは大変驚きました。最適化ソルバー (CBC) は優秀ですね。
●最大被覆問題
施設設置問題における「最大被覆問題 (max cover problem)」は、あらかじめ設置する施設の個数 (p) を決めておいて、できるだけ多くの利用者をカバーするような設置場所を求める問題です。簡単な例題として、設置する施設の個数が 2 つで、利用者 \(D_{i}\) が利用できる施設の候補地 \(F_{j}\) が下表のように与えられているとき、利用者の総和が最大となる設置場所を求めてみましょう。
表 : 利用可能な施設
: f0 : f1 : f2 : f3 : f4
--------+----+----+----+----+----
d0 (1) : 1 : 0 : 0 : 0 : 1
d1 (4) : 1 : 1 : 0 : 0 : 0
d2 (5) : 0 : 1 : 1 : 0 : 0
d3 (3) : 0 : 0 : 1 : 1 : 0
d4 (2) : 0 : 0 : 0 : 1 : 1
カッコ内の数字は人数
(出典 : 参考 URL 2『ロジスティクス工学 05 施設配置』)
施設 \(f_{i}\) の選択を表す変数 (Binary) を \(F_{i}\), 利用者 \(d_{i}\) が施設を利用できるか否かを表す変数 (Binary) を \(X_{i}\), 利用者の人数を \(D_{i}\) とし、上表の要素を \(W_{ij}\) で表すことにします。目的関数と制約条件は次のようになります。
\( \displaystyle \sum_i D_{i} X_{i} \)
\(\begin{array}{l} \displaystyle \sum_j F_{j} = 2 \\ \displaystyle \sum_j W_{ij} F_{j} \leq X_{i} \quad (i= 0, 1, 2, 3, 4) \end{array}\)
目的関数は簡単ですね。制約条件ですが、最初の式は設置する施設の数を表します。次の式は、\(X_{i}\) が 1 ならば施設を利用できるので、左辺式の値は 1 以上になることを表しています。\(X_{i}\) が 0 ならば施設を利用できないので、左辺式は 0 でもいいわけです。
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 最大被覆問題 (max cover)
import pulp
prob = pulp.LpProblem('max-cover', sense = pulp.LpMaximize)
# 利用可能な施設
# f0 f1 f2 f3 f4
ws = [[ 1, 0, 0, 0, 1], # d0
[ 1, 1, 0, 0, 0], # d1
[ 0, 1, 1, 0, 0], # d2
[ 0, 0, 1, 1, 0], # d3
[ 0, 0, 0, 1, 1]] # d4
# 利用者の人数
ds = [1, 4, 5, 3, 2]
# 変数
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(5)]
xs = [pulp.LpVariable('x{}'.format(i), cat='Binary') for i in range(5)]
# 目的関数
prob += pulp.lpDot(ds, xs)
# 制約条件
prob += pulp.lpSum(fs) == 2
for i in range(5):
prob += pulp.lpDot(ws[i], fs) >= xs[i]
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([f.value() for f in fs])
print([x.value() for x in xs])
print(prob.objective.value())
Status Optimal [0.0, 1.0, 0.0, 1.0, 0.0] [0.0, 1.0, 1.0, 1.0, 1.0] 14.0
設置する施設は f1 と f3 で、d1 から d4 までの計 14 人をカバーすることができます。残念ながら d0 の人は施設を利用することはできません。
次は、利用者 (一人) を平面上にランダムに n 個配置し、半径 r 内にある施設を利用できる条件で、最大被覆問題を解いてみましょう。施設は利用者の中から選びます。プログラムは次のようになります。
リスト : 最大被覆問題 (乱数による配置)
def solver_max(ps, r, p):
size = len(ps)
ws = make_matrix(ps, r) # 行列
prob = pulp.LpProblem('max-cover', sense = pulp.LpMaximize)
# 変数の生成
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
xs = [pulp.LpVariable('x{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum(xs)
# 制約条件
prob += pulp.lpSum(fs) == p
for i in range(size):
prob += pulp.lpDot(ws[i], fs) >= xs[i]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
z = prob.objective.value()
print(z, z / size)
print(time.time() - s)
draw(ps, fs, r)
# 実行
for n in [25, 50, 75, 100]:
print("-----", n, "-----")
solver_max(make_data(n), 100, 7)
関数 make_matrix() は集合被覆問題で作成したものと同じです。プログラムは簡単なので説明は割愛いたしhます。
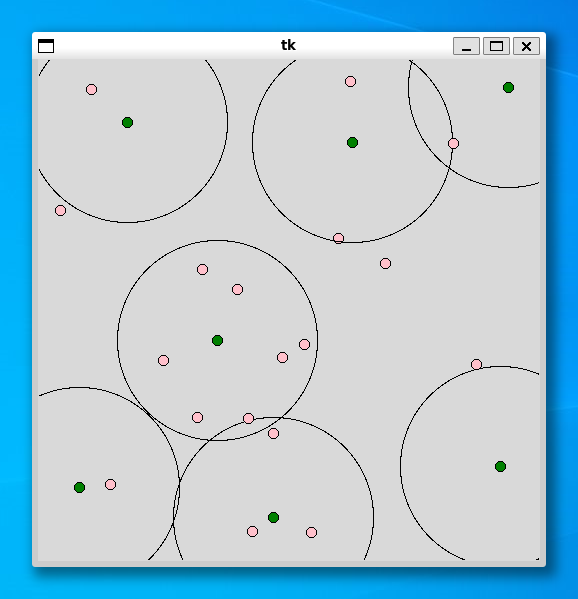
それでは実行してみましょう。半径 r は 100 で、設置する施設数 p は 7 としました。
----- 25 ----- Status Optimal 22.0 0.88 0.027833938598632812
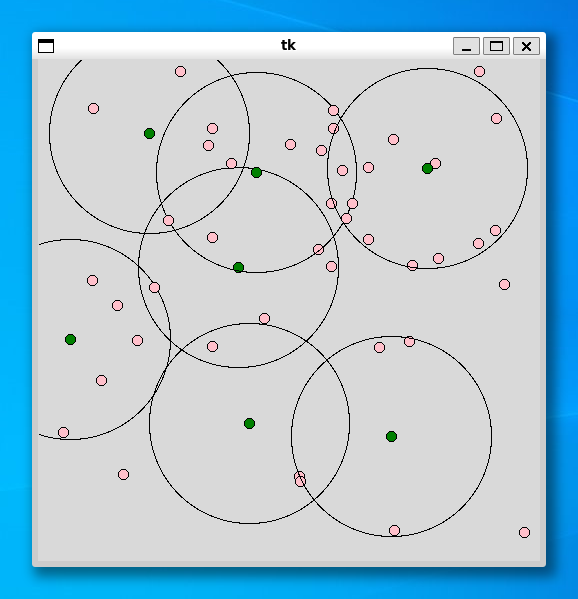
----- 50 ----- Status Optimal 46.0 0.92 0.024124622344970703
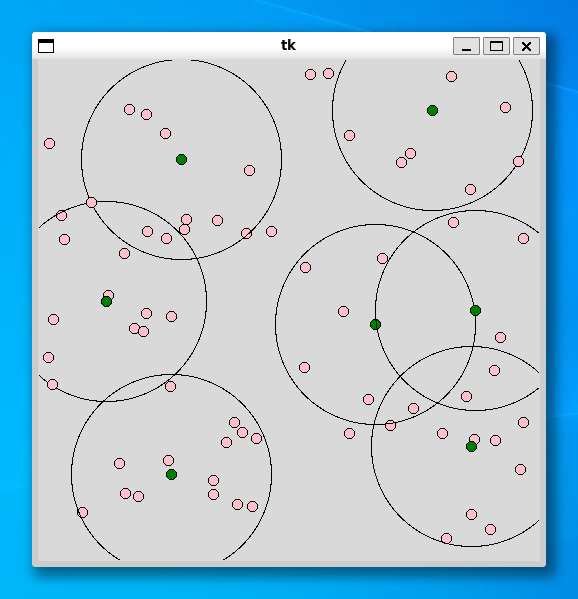
----- 75 ----- Status Optimal 70.0 0.9333333333333333 0.016228914260864258
----- 100 ----- Status Optimal 92.0 0.92 0.019514083862304688
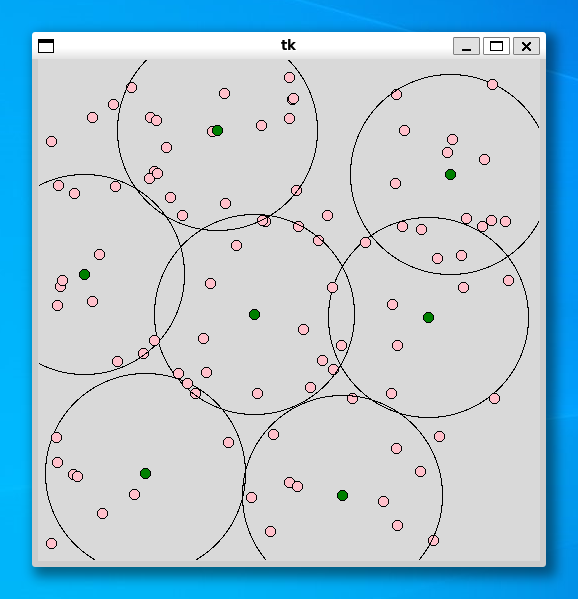
集合被覆問題と同じように、利用者の個数が 100 個でもすぐに解を求めることができました。興味のある方は、施設の個数や半径を変更するなど、いろいろ試してみてください。
●参考 URL
- 数理最適化入門(4):施設配置の数理モデル [PDF], (田中健一さん)
- ロジスティクス工学 05 施設配置 [PDF], (宮本裕一郎さん)
- 集合被覆問題 - Wikipedia
●プログラムリスト
#
# cover.py : 集合被覆問題と最大被覆問題 (乱数版)
#
# Copyright (C) 2019-2023 Makoto Hiroi
#
import sys, math, time, random
import pulp
import tkinter as tk
# 乱数でデータを生成
def make_data(n):
return [(random.randrange(480) + 10, random.randrange(480) + 10) for _ in range(n)]
# 描画
def draw(ps, fs, r):
root = tk.Tk()
c0 = tk.Canvas(root, width = 500, height = 500)
c0.pack()
for k, (i, j) in zip(fs, ps):
if k.value() == 1:
c0.create_oval(i - 5, j - 5, i + 5, j + 5, fill = 'green')
c0.create_oval(i - r, j - r, i + r, j + r)
else:
c0.create_oval(i - 5, j - 5, i + 5, j + 5, fill = 'pink')
root.mainloop()
# 標準入力よりデータを読み込む
def read_data():
buff = []
for a in sys.stdin:
b = a.split()
buff.append((int(b[0]), int(b[1])))
return buff
# 距離を求める
def distance(p1, p2):
dx = p1[0] - p2[0]
dy = p1[1] - p2[1]
return math.sqrt(dx * dx + dy * dy)
# 行列の生成
def make_matrix(ps, r):
def check(l):
if l <= r:
return 1
else:
return 0
return [[check(distance(p1, p2)) for p2 in ps] for p1 in ps]
# 集合被覆問題
def solver_set(ps, r):
size = len(ps)
cs = make_matrix(ps, r) # 行列
prob = pulp.LpProblem('set-cover')
# 変数の生成
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum(fs)
# 制約条件
for c in cs:
prob += pulp.lpDot(c, fs) >= 1
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print("z", prob.objective.value())
print(time.time() - s)
draw(ps, fs, r)
# 最大被覆問題
def solver_max(ps, r, p):
size = len(ps)
ws = make_matrix(ps, r) # 行列
prob = pulp.LpProblem('max-cover', sense = pulp.LpMaximize)
# 変数の生成
fs = [pulp.LpVariable('f{}'.format(i), cat='Binary') for i in range(size)]
xs = [pulp.LpVariable('x{}'.format(i), cat='Binary') for i in range(size)]
# 目的関数
prob += pulp.lpSum(xs)
# 制約条件
prob += pulp.lpSum(fs) == p
for i in range(size):
prob += pulp.lpDot(ws[i], fs) >= xs[i]
s = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
z = prob.objective.value()
print(z, z / size)
print(time.time() - s)
draw(ps, fs, r)