●地図の配色問題
今回は、Puzzle DE Programming で取り上げた「地図の配色問題」を PuLP で解いてみましょう。地図の配色問題は、平面上にある隣り合った地域が同じ色にならないように塗り分けるという問題です。1976 年にアッペルとハーケンにより、どんな場合でも 4 色あれば塗り分けできることが証明されました。これを「四色問題」といいます。
┌─────────┐ │ a │ ├──┬───┬──┤ │ b │ c │ d │ ├──┴─┬─┴──┤ │ e │ f │ └────┴────┘ 図 : 簡単な地図
今回は、図に示す簡単な地図を 4 色で塗り分けてみます。地図は参考文献『Prolog の技芸』から引用しました。
PuLP で地図の配色問題を解く場合、地図をグラフとして考えます。領域 a, b, c, d, e, f を頂点 (0, 1, 2, 3, 4, 5) とし、隣接している頂点を辺で結びます。頂点の色は変数 \(X_{ij}\) (Binary) で表します。頂点 i が色 j で塗られるならば \(X_{ij}\) は 1 になり、そうでなければ 0 とします。使用する色は変数 \(Y_{j}\) (Binary) で表します。色 j を使用した場合、\(Y_{j}\) の値は 1 になり、そうでなければ 0 とします。
目的関数と制約条件は次のようになります。
\( \displaystyle \sum_j Y_{j} \)
1. 頂点に塗られる色は一つ
\( \displaystyle \sum_j X_{ij} = 1 \)
2. 色 j が未使用 (0) ならば \(X_{ij}\) も 0
\( X_{ij} \leq Y_{j} \)
3. 辺 (i, j) の頂点 i, j の色は異なる
\( X_{ik} + X_{jk} \leq 1 \)
目的関数は簡単ですね。これを最小化することで、最も少ない色で地図を塗り分けることができます。制約条件ですが、最後の式が隣接した頂点の色が異なることを表しています。頂点 i, j が両方とも色 k で塗られている場合、\(X_{ik}\) と \(X_{ik}\) の値は 1 になります。すると、左辺式の値は 2 になるので、制約条件は不成立になります。条件を満たす場合は、どちらかの変数が 1 か両方の変数が 0 のときだけです。
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 地図の配色問題
import pulp
# 辺
edge = [
(0, 1), (0, 2), (0, 3),
(1, 2), (1, 4),
(2, 3), (2, 4), (2, 5),
(3, 5), (4, 5)
]
# 頂点の個数
size = 6
# 色の最大数
max_color = 4
prob = pulp.LpProblem('coloring')
# 変数
xs = []
for n in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(n, i), cat = 'Binary') for i in range(max_color)]
xs.append(xs1)
ys = [pulp.LpVariable('y{}'.format(i), cat = 'Binary') for i in range(max_color)]
# 目的関数 (最小化)
prob += pulp.lpSum(ys)
# 制約条件
for x in xs:
prob += pulp.lpSum(x) == 1 # 頂点には必ず色が塗られる
for i in range(size):
for j in range(max_color):
prob += xs[i][j] <= ys[j] # 色 j が塗られない場合、xs[i][j] は 0 になる
for i, j in edge:
for k in range(max_color):
prob += xs[i][k] + xs[j][k] <= 1 # 隣接する頂点は同じ色にならない
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
for xs1 in xs:
print([x.value() for x in xs1])
print(prob.objective.value())
Status Optimal [0.0, 0.0, 0.0, 1.0] [0.0, 0.0, 1.0, 0.0] [0.0, 1.0, 0.0, 0.0] [0.0, 0.0, 1.0, 0.0] [0.0, 0.0, 0.0, 1.0] [1.0, 0.0, 0.0, 0.0] 4.0
頂点の色は a = 3, b = 2, c = 1, d = 2, e = 3, f = 0 になり、四色で塗り分けることができました。
●参考文献・URL
- Leon Sterling, Ehud Shapiro, 『Prolog の技芸』, 共立出版, 1988
- グラフの彩色数問題の IP ソルバを用いた高速化手法の提案 [PDF], (牧井慶太朗さん, リンク切れ)
●グラフ彩色問題
「グラフ彩色 (Graph coloring)」は、隣接する頂点の色が同じにならないように、すべての頂点を塗り分けることをいいます。これを「頂点彩色」といいます。頂点のほかに、辺についても同様のことを考えることができます。これを「辺彩色」といいます。グラフ彩色というと、頂点彩色のことを指すのが一般的なようです。前回取り上げた「地図の配色問題」は頂点彩色問題のひとつです。今回は頂点彩色問題を取り上げます。
基本的な考え方は「地図の配色問題」と同じですが、彩色数の上限値が問題になります。完全グラフ (任意の頂点間に辺が存在するグラフ) の場合、彩色数は頂点の個数 n と一致しますが、一般的なグラフでは n よりも小さな値になるでしょう。彩色数の上限値が厳密解に近ければ、最適化ソルバーの実行時間を短縮することができるかもしれません。そこで、今回は「貪欲法」で彩色数の上限値を求めることにします。
●Welsh-Powell のアルゴリズム
貪欲法での彩色アルゴリズムは簡単です。
- 頂点の集合に順番 \(v_{0}, \ldots, v_{i}, \ldots, v_{n-1}\) を付ける
- 頂点 \(v_{i}\) の色を決めるとき、\(v_{0}\) から \(v_{i-1}\) までの頂点は k 色で塗り分けられているとする
- \(v_{i}\) と隣接する頂点が k 色で塗り分けられるならば、その中の最小値を \(v_{i}\) に塗る
- そうでなければ、新しい色 k + 1 を \(v_{i}\) に塗る
- 次の頂点 \(v_{i+1}\) の色を決める (2 に戻る)
- すべての頂点の色が決まれば終了
1 の順序付けですが、次数 (頂点に接続されている辺の本数) の大きい方から順番に行う方法を「Welsh-Powell のアルゴリズム」といいます。この場合、最大色数は最悪でもグラフの最大次数 + 1 になることが知られています。
プログラムは次のようになります。
リスト : 貪欲彩色
# 隣接リスト
def make_adjacent(edge, n):
xs = [[] for _ in range(n)]
for i, j in edge:
xs[i].append(j)
xs[j].append(i)
return xs
# 貪欲法
def greedy_coloring(edge, n):
xs = make_adjacent(edge, n)
ys = [0] * n
max_color = 0
for i in sorted(range(n), key = lambda x: -len(xs[x])):
cs = [ys[j] for j in xs[i]]
c = 1
while c in cs: c += 1
ys[i] = c
if max_color < c: max_color = c
return max_color, ys
関数 greedy_coloring() の引数 edge は辺を格納したコレクション、n は頂点の個数です。頂点は正整数 (0 - n-1) で表し、辺は両端の頂点 i, j (i < j) を格納したタプル (i, j) で表します。
最初に、関数 make_adjacent() で隣接リストを生成し、変数 xs にセットします。変数 ys は色を格納した配列 (Python のリスト) です。0 は色が塗られていないことを表します。変数 max_color は最大色数を格納します。次の for ループで頂点を順番に取り出して色を決めていきます。このとき、関数 sorted() で次数の降順で頂点をソートします。頂点 x の次数は len(xs[x]) で簡単に求めることができます。今回は降順にソートするので、負の値を比較することに注意してください。
色を決定する処理も簡単です。頂点 i に隣接する頂点の色を取り出して変数 cs にセットします。変数 c は色を表します。c の値を 1 からひとつずつ増やしていき、その値が cs に含まれていなければ、ys[i] に c をセットします。c が max_color よりも大きくなったならば、max_color の値を c に更新します。最後に max_color と ys を返します。
簡単な実行例を示しましょう。
>>> import color >>> edge = [ ... (0, 1), (0, 2), (0, 3), ... (1, 2), (1, 4), ... (2, 3), (2, 4), (2, 5), ... (3, 5), (4, 5) ... ] >>> color.make_adjacent(edge, 6) [[1, 2, 3], [0, 2, 4], [0, 1, 3, 4, 5], [0, 2, 5], [1, 2, 5], [2, 3, 4]] >>> color.greedy_coloring(edge, 6) (4, [2, 3, 1, 3, 2, 4])
edge は「地図の配色問題」で取り上げた地図と同じデータです。このように、greedy_coloring() でも最適解が求まる場合もあります。
●テストデータの生成
次はテストデータを生成する関数 make_edge() を作ります。
リスト : テストデータの生成
def make_edge(n):
edge = set()
size = int(n * (n - 1) / 2 * 0.3) # 辺密度 30 %
# 0 から n - 1 までの巡回路
for i in range(n - 1):
edge.add((i, i+1))
edge.add((0, n - 1))
while len(edge) <= size:
i = random.randrange(n)
j = random.randrange(n)
if i == j:
continue
elif i > j:
i, j = j, i
edge.add((i, j))
return edge
make_edge() の引数 n は頂点の個数です。edge は辺を格納するセット (集合) です。辺の本数は完全グラフが最大で、その値は n * (n - 1) / 2 になります。辺密度とは、グラフの辺の本数を n * (n - 1) / 2 で割った値です。今回は辺密度が 30 % になるように辺を生成します。
最初に 0 から n - 1 までの巡回路を作ります。次の while ループで、頂点 i, j を乱数で選び、それが同じ値でなければ edge に追加します。このとき i > j であれば、i と j の値を交換します。Python のセットは重複要素を許さないので、同じ辺が格納されることはありません。あと辺の本数が size になるまで処理を繰り返すだけです。
●解法プログラム
PuLP による解法プログラムは次のようになります。
リスト : グラフ彩色問題
def solver(edge, size):
prob = pulp.LpProblem('coloring')
# 貪欲法
max_color, _ = greedy_coloring(edge, size)
print("edge =", len(edge), "greedy =", max_color)
# 変数
xs = []
for n in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(n, i), cat = 'Binary') for i in range(max_color)]
xs.append(xs1)
ys = [pulp.LpVariable('y{}'.format(i), cat = 'Binary') for i in range(max_color)]
# 目的関数 (最小化)
prob += pulp.lpSum(ys)
# 制約条件
for x in xs:
prob += pulp.lpSum(x) == 1 # 頂点には必ず色が塗られる
for i, j in edge:
for k in range(max_color):
prob += xs[i][k] + xs[j][k] <= 1 # 隣接する頂点は同じ色にならない
for i in range(size):
for j in range(max_color):
prob += xs[i][j] <= ys[j] # 色 j が塗られない場合、xs[i][j] は 0 になる
start = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([y.value() for y in ys])
print(prob.objective.value())
print(time.time() - start)
# 実行
for n in [15, 20, 25, 30, 35]:
print("-----", n, "-----")
xs = make_edge(n)
solver(xs, n)
目的関数と制約条件は「地図の配色問題」のプログラムと同じです。大きな違いは、色の上限値 max_color を関数 greedy_coloring() で求めているところです。あとはとくに難しいところはないと思います。
それでは実行してみましょう。
----- 15 ----- edge = 32 greedy = 4 Status Optimal [1.0, 1.0, 1.0, 1.0] 4.0 0.03456687927246094 ----- 20 ----- edge = 58 greedy = 4 Status Optimal [1.0, 1.0, 1.0, 1.0] 4.0 0.05794882774353027 ----- 25 ----- edge = 91 greedy = 6 Status Optimal [1.0, 0.0, 1.0, 1.0, 1.0, 1.0] 5.0 8.245569944381714 ----- 30 ----- edge = 131 greedy = 6 Status Optimal [1.0, 1.0, 1.0, 1.0, 0.0, 1.0] 5.0 0.250288724899292 ----- 35 ----- edge = 179 greedy = 5 Status Optimal [1.0, 1.0, 1.0, 1.0, 1.0] 5.0 3.453038454055786
- 実行環境 : Python 3.10.6, PuLP 2.7.0, Ubunts 22.04 LTS (WSL2, Windows 10), Intel Core i5-6200U 2.30GHz
頂点の個数が 25 個程度でもちょっと時間がかかりますね。グラフ彩色問題は解くのが難しい問題であることがわかります。頂点の個数が増えると、解くまでに時間がかかるようになりますが、辺密度によっても実行時間は左右されます。興味のある方はいろいろ試してみてください。
●参考文献・URL
- グラフの彩色数問題の IP ソルバを用いた高速化手法の提案 [PDF], (牧井慶太朗さん, リンク切れ)
- グラフ彩色 - Wikipedia
●プログラムリスト
#
# color.py : グラフ彩色問題 (辺を乱数で選ぶ)
#
# Copyright (C) 2019-2023 Makoto Hiroi
#
import random, time
import pulp
# 乱数で辺を結ぶ
def make_edge(n):
edge = set()
size = int(n * (n - 1) / 2 * 0.3) # 辺密度 30 %
# 0 から n - 1 までの巡回路
for i in range(n - 1):
edge.add((i, i+1))
edge.add((0, n - 1))
while len(edge) <= size:
i = random.randrange(n)
j = random.randrange(n)
if i == j:
continue
elif i > j:
i, j = j, i
edge.add((i, j))
return edge
# 隣接リスト
def make_adjacent(edge, n):
xs = [[] for _ in range(n)]
for i, j in edge:
xs[i].append(j)
xs[j].append(i)
return xs
# 貪欲法
def greedy_coloring(edge, n):
xs = make_adjacent(edge, n)
ys = [0] * n
max_color = 0
for i in sorted(range(n), key = lambda x: -len(xs[x])):
cs = [ys[j] for j in xs[i]]
c = 1
while c in cs: c += 1
ys[i] = c
if max_color < c: max_color = c
return max_color, ys
# 解法
def solver(edge, size):
prob = pulp.LpProblem('coloring')
# 貪欲法
max_color, _ = greedy_coloring(edge, size)
print("edge =", len(edge), "greedy =", max_color)
# 変数
xs = []
for n in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(n, i), cat = 'Binary') for i in range(max_color)]
xs.append(xs1)
ys = [pulp.LpVariable('y{}'.format(i), cat = 'Binary') for i in range(max_color)]
# 目的関数 (最小化)
prob += pulp.lpSum(ys)
# 制約条件
for x in xs:
prob += pulp.lpSum(x) == 1 # 頂点には必ず色が塗られる
for i, j in edge:
for k in range(max_color):
prob += xs[i][k] + xs[j][k] <= 1 # 隣接する頂点は同じ色にならない
for i in range(size):
for j in range(max_color):
prob += xs[i][j] <= ys[j] # 色 j が塗られない場合、xs[i][j] は 0 になる
start = time.time()
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([y.value() for y in ys])
print(prob.objective.value())
print(time.time() - start)
# 実行
for n in [15, 20, 25, 30, 35]:
print("-----", n, "-----")
xs = make_edge(n)
solver(xs, n)
●線形回帰
2 つのデータの間にある関連性のことを「相関」といい、一方が増加するにつれて他方も増加するまたは減少する傾向が見られるとき、相関関係 (または単に相関) があるといいます。
2 つのデータの間に相関が認められるとき、その関係を曲線や曲面で代表することを「回帰 (regression)」といいます。とくに、相関が線形傾向の場合、その関係を一本の直線で示すことができます。これを「直線回帰」とか「線形回帰」といい、その直線を「回帰直線」といいます。
線形回帰は「最小二乗法」で求めることができますが、最適化ソルバーを使って求めることも可能です。今回は簡単な例題として、東京の年平均気温が今後どの程度上昇するか、回帰を用いて推定してみましょう。データは気象庁「年ごとの値 (東京)」の 1975 年から 2018 年までの年平均気温を用いました。
線形回帰は 2 つのデータ \(X\) と \(Y\) の関係を一次式 \(Y = a \times X + b\) で近似します。求める値は a と b です。実際のデータを \(X_{i}, Y_{i}\) とすると、回帰直線から計算した値 \(a \times X_{i} + b\) と実際のデータ \(Y_{i}\) には誤差があります。これを \(Z_{i}\) としましょう。
目的関数は誤差の合計値を最小にすることになります。
\( \displaystyle \sum_i Z_{i} \)
次に制約条件ですが、PuLP では絶対値を求める関数 abs() を使うことができないので、次のように式に分けて条件を表します。
\(\begin{array}{ll} 1. & Y_{i} - (a \times X_{i}) \geq -Z_{i} \\ 2. & Y_{i} - (a \times X_{i}) \leq Z_{i} \\ 3. & Z_{i} \geq 0 \end{array}\)
条件式 3 で \(Z_{i}\) に非負条件を設定し、\(Y_{i} - (a \times X_{i})\) が \(-Z_{i}\) 以上 \(Z_{i}\) 以下であることを条件式 1, 2 で表します。たとえば、誤差が \(-Z_{i}\) の場合、1 が成立するとともに、2 は \(-Z_{i} \lt Z_{i}\) になるので成立します。逆に、誤差が \(Z_{i}\) の場合、2 が成立するとともに 1 は \(Z_{i} \gt -Z_{i}\) になるので、これも成立します。これで絶対値を表すことができます。
あとはこれを PuLP でプログラムするだけです。プログラムリストと実行結果を示します。
リスト : 回帰直線
import pulp
import matplotlib.pyplot as plt
# 東京の年平均気温 (1975 - 2018)
data = [
15.6, 15.0, 15.8, 16.1, 16.9, 15.4, 15.0, 16.0, 15.7, 14.9,
15.7, 15.2, 16.3, 15.4, 16.4, 17.0, 16.4, 16.0, 15.5, 16.9,
16.3, 15.8, 16.7, 16.7, 17.0, 16.9, 16.5, 16.7, 16.0, 17.3,
16.2, 16.4, 17.0, 16.4, 16.7, 16.9, 16.5, 16.3, 17.1, 16.6,
16.4, 16.4, 15.8, 16.8
]
xs = range(1975, 2019)
prob = pulp.LpProblem('regression')
# 変数
zs = [pulp.LpVariable('z{}'.format(i), lowBound=0) for i in xs]
a = pulp.LpVariable('a')
b = pulp.LpVariable('b')
# 目的関数
prob += pulp.lpSum(zs)
# 制約条件
for x, y in zip(xs, data):
prob += y - (a * x + b) >= -zs[x - 1975]
prob += y - (a * x + b) <= zs[x - 1975]
# 解法
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print(a.value(), b.value())
print(prob.objective.value())
# 散布図
plt.plot(xs, data, 'o')
# 回帰直線
plt.plot(range(1975, 2040), [a.value() * x + b.value() for x in range(1975,2040)])
# グラフの表示
plt.show()
Status Optimal 0.021621622 -26.945946 18.329729814000004
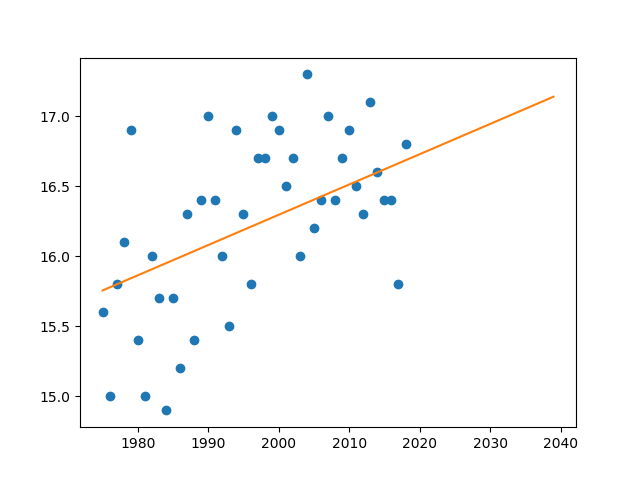
グラフの描画には Python のライブラリ matpoltlib を使いました。回帰直線は Y = 0.0216 * X - 26.95 になりました。今後もこの傾向が続くと仮定すると、東京の平均気温が 18 度になるのは 2080 年頃になりそうです。
なお、この結果は単純な線形回帰での推定にすぎず、実際の予測にはもっと複雑なモデルが使われていることでしょう。あくまでも回帰の例題ということで、結果については本気にしないようお願いいたします。
ところで、線形回帰は Python のライブラリ NumPy のほうが簡単に求めることができます。興味のある方は拙作のページ「お気楽 NumPy プログラミング超入門: 基本的な統計処理」をお読みくださいませ。
●参考 URL
- 線形回帰 - Wikipedia
- Algorithms with Python: 統計学の基礎知識 [3], (広井誠)
●ジョブショップ問題
スケジューリング問題 (scheduling problem) は、多くの仕事 (ジョブ) をいろいろな制約のもとで実行するとき、実行可能なスケジュールや最適なスケジュールを求める問題です。ジョブショップ問題 (job shop problem) はスケジューリング問題の一種で、限られた機械を用いて多数のジョブを実行するとき、目的関数 (仕事の完了時刻や納期遅れなど) が最小となるよう、機械に投入するジョブの順序を決定する問題です。
ジョブショップ問題にはいろいろな種類がありますが、今回は最も基本的な「1機械問題 (one-machine problem)」を取り上げます。これはすべてのジョブを 1 台の機械で処理するとき、処理するジョブの順番を決定する問題です。
4 つのジョブを 1 台の機械で処理します。ジョブに関するデータが下表のように与えらているとき、重み付き完了時刻和が最小となるジョブの処理順序を求めてください。なお、機械は同時に 2 つ以上のジョブを処理することはできず、一度処理を開始したら完了するまで処理を中断できないものとします。
表 : ジョブのデータ
ジョブ番号 : 0 : 1 : 2 : 3
-----------+---+---+---+---
重み W : 2 : 1 : 3 : 5
処理時間 P : 3 : 2 : 5 : 7
出典 : 『整数計画法による定式化入門』(参考文献 1)
ジョブ i の重みを \(W_{i}\), 完了時刻を \(C_{i}\) とすると、重み付き完了時刻和 Z は次式で表されます。
この問題の目的関数は重み付き完了時刻和 Z になります。制約条件ですが、次のようになります。
\(\begin{array}{ll} 1. & C_{i} \geq P_{i} \\ 2. & C_{j} \geq C_{i} + P_{j} \ \mathrm{or} \ C_{i} \geq C_{j} + P_{i} \end{array}\)
ジョブを最初に処理する場合、式 1 の等号が成り立ちます。ジョブが 2 番目以降に処理されるならば、式 1 は無条件に成立します。式 2 は論理和 (or) になっていて、ジョブ i が j よりも先に処理されるならば左辺が成り立ち、逆に j が i よりも先に処理されるならば右辺が成り立ちます。
PuLP では制約条件の定義に論理和を使うことはできないので、ジョブの前後関係を表す変数 (Binary) \(X_{ij}\) と M (大きな定数) を使って、式 2 を次のように書き直します。
\(i, j = 0, \ldots, n - 1, i \ne j\)
ジョブ i が j よりも先に処理される場合、\(X_{ij}\) の値は 1 で、そうでなければ 0 とします。式 2a は \(X_{ij}\) が 1 ならば式 2 の左辺と同じなので、条件を満たすことが分かります。\(X_{ij}\) が 0 ならば、2a の右辺は \(M\) になります。このとき、左辺の値は正になるので、\(M\) が十分に大きな値であれば条件を満たします。式 2b は簡単で、\(X_{ij}\) が 1 ならば \(X_{ji}\) は 0 で、\(X_{ij}\) が 0 ならば \(X_{ji}\) は 1 になります。これで論理和を表すことができます。
あとはこれを PuLP でプログラムするだけです。
リスト : ジョブショップ問題 (1機械問題)
import pulp
# job の数
size = 4
# 重み
ws = [2, 1, 3, 5]
# 所要時間
ps = [3, 2, 5, 7]
prob = pulp.LpProblem('one-machine')
# 変数
# 終了時刻
cs = [pulp.LpVariable('c{}'.format(i), lowBound=0) for i in range(size)]
# xs[i][j] = 1 ならば i は j に先行、0 ならば i は j の後
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat="Binary") for j in range(size)]
xs.append(xs1)
# 目的関数
prob += pulp.lpDot(ws, cs)
# 制約条件
for i in range(size):
prob += cs[i] >= ps[i]
for j in range(size):
if i == j: continue
prob += cs[i] - cs[j] + ps[j] <= 99 * (1 - xs[i][j])
prob += xs[i][j] + xs[j][i] == 1
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([c.value() for c in cs])
print(prob.objective.value())
大きな定数 M は 99 としました。あとは目的関数と制約条件をそのままプログラムしただけなので、とくに難しいところはないと思います。実行結果は次のようになりました。
Status Optimal [10.0, 17.0, 15.0, 7.0] 117.0
ジョブの順番は 3, 0, 2, 1 で、Z の値は 117 になりました。
●納期遅れの最小化
次は納期の遅れが最小となるジョブの処理順序を求めてみましょう。
4 つのジョブを 1 台の機械で処理します。ジョブに関するデータが下表のように与えらているとき、納期遅れの総和が最小となるジョブの処理順序を求めてください。なお、機械は同時に 2 つ以上のジョブを処理することはできず、一度処理を開始したら完了するまで処理を中断できないものとします。また、納期より速くジョブが終了した場合、納期遅れは 0 とします。
表 : ジョブのデータ
ジョブ番号 : 0 : 1 : 2 : 3
-----------+---+---+---+----
納期 D : 4 : 3 : 7 : 10
処理時間 P : 3 : 2 : 5 : 7
ジョブの完了時刻を C_{i}, 納期を D_{i} とすると、目的関数は次のようになります。
\( \displaystyle \sum_i \max(C_{i} - D_{i}, 0) \)
max() は引数を比較して大きいほうの値を返す関数です。PuLP では目的関数や制約条件の定義に max() を使用できないので、納期遅れを表す変数 T_{i} を導入して、目的関数と制約条件を書き直すことにします。
\( Z = \displaystyle \sum_i T_{i} \)
\(\begin{array}{ll} 1. & C_{i} \geq P_{i} \\ 2. & C_{i} - C_{j} + P_{j} \leq M * (1 - X_{ij}) \\ 3. & X_{ij} + X_{ji} = 1 \\ 4. & C_{i} - D_{i} \leq T_{i} \\ 5. & T_{i} \geq 0 \end{array}\)
\(i, j = 0, \ldots, n - 1, i \ne j\)
目的関数は簡単ですね。制約条件では式 4, 5 を新しく追加しています。式 5 で変数 \(T_{i}\) に非負条件を設定します。式 4 ですが、納期に間に合うと左辺は 0 以下の値になるので、変数 \(T_{i}\) の値は 0 になります。納期に送れると左辺は 0 より大きな値になるので、それが変数 \(T_{i}\) の値になります。これで納期に遅れたジョブの時間だけをカウントすることができます。
プログラムと実行結果を示します。
リスト : 納期遅れの最小化
import pulp
# job の数
size = 4
# 納期
ds = [4, 3, 7, 10]
# 所要時間
ps = [3, 2, 5, 7]
prob = pulp.LpProblem('one-machine')
# 変数
# 終了時刻
cs = [pulp.LpVariable('c{}'.format(i), lowBound=0) for i in range(size)]
# 遅延時間
ts = [pulp.LpVariable('t{}'.format(i), lowBound=0) for i in range(size)]
# xs[i][j] = 1 ならば i は j に先行、0 ならば i は j の後
xs = []
for i in range(size):
xs1 = [pulp.LpVariable('x{}_{}'.format(i, j), cat="Binary") for j in range(size)]
xs.append(xs1)
# 目的関数
prob += pulp.lpSum(ts)
# 制約条件
for i in range(size):
prob += cs[i] >= ps[i]
prob += cs[i] - ds[i] <= ts[i]
for j in range(size):
if i == j: continue
prob += cs[i] - cs[j] + ps[j] <= 99 * (1 - xs[i][j])
prob += xs[i][j] + xs[j][i] == 1
status = prob.solve(pulp.PULP_CBC_CMD(msg=0))
print("Status", pulp.LpStatus[status])
print([c.value() for c in cs])
print([t.value() for t in ts])
print(prob.objective.value())
Status Optimal [5.0, 2.0, 10.0, 17.0] [1.0, 0.0, 3.0, 7.0] 11.0
ジョブの順番は 1, 0, 2, 3 で、納期遅れの総和は 11 になりました。
●参考 URL
- 整数計画法による定式化入門 (PDF), (藤江哲也さん)