●Hello, SymPy!!
- SymPy は Python で数式処理システムのような記号計算を行うためのライブラリ
- 記号計算とは、数学で数式を計算するのと同様な計算を行うこと
- たとえば、f(x) = x2 の微分は f'(x) = 2x になるが、SymPy を使うと同じように計算できる
>>> import sympy as sy
>>> x = sy.Symbol('x')
>>> f = x**2 + 2*x + 1
>>> f
x**2 + 2*x + 1
>>> g = f.diff()
>>> g
2*x + 2
python3 -m pip install sympy
$ python3 -m pip freeze | grep sympy sympy==1.12 $ python3 -m pip freeze | grep mpmath mpmath==1.3.0
- 実行環境 : Python 3.10.6, Ubunts 22.04 LTS (WSL2 + WSLg, Windows 10), Intel Core i5-6200U 2.30GHz
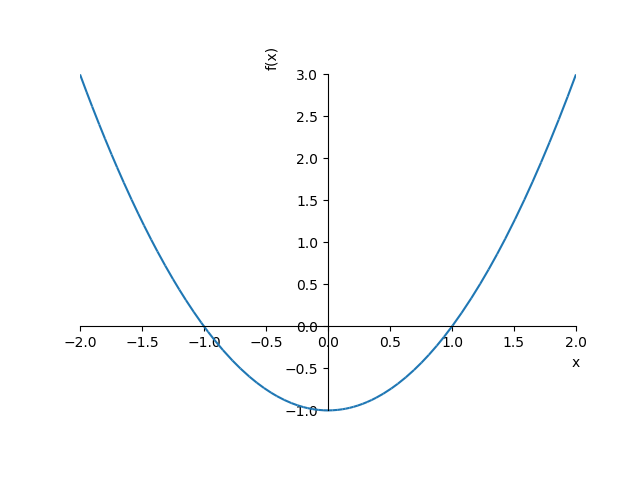
>>> f = x**2 - 1 >>> sy.plotting.plot(f, (x, -2, 2)) <sympy.plotting.plot.Plot object at 0x7f91ffedff40>
python3 -m pip install matplotlib
$ python3 -m pip freeze | grep matplotlib matplotlib==3.6.2
- SymPy, (本家)
- Welcome to SymPy’s documentation!, (本家)
- 3.2. Sympy : Python での代数計算, (Scipy Lecture Notes)
- Pythonで数学の勉強:代数基礎(数式と関数), (@tibigame さん)
- SymPy - Wikipedia
●SymPy の基本
- 数
- SymPy の数は整数 (多倍長整数)、有理数、浮動小数点数 (任意精度)、複素数
- 整数は Integer() で、浮動小数点数 Float() で生成できるが、Python の整数と浮動小数点数を使うこともできる
- Python の整数と浮動小数点数は自動的に SymPy のそれに変換される
- 有理数は Rational(p, q), p: 分子, q: 分母, p, q は多倍長整数
- Python3 の場合、除算 / の結果は浮動小数点数になる
- 整数同士の割り算で整数値を求めるには // を使う
- SymPy で a, b が整数 (Integer) の場合、a / b は有理数になる
- SymPy の虚数単位は I になる
- Python には複素数を表すデータ型 (complex) があるが SymPy にはない
- SymPy は虚数単位を含む数式を複素数として扱う
- 基本的な演算は Python と同じ (+, -, *, /, //, %, **)
- 定数と数学関数
- SymPy では特殊な定数 (E, pi, oo) や数学関数を数式として扱う
- E : 自然対数の底 (ネイピア数)
- pi : 円周率
- oo : 無限大
>>> import sympy as sy
>>> sy.Integer(12345)
12345
>>> sy.Integer('12345')
12345
>>> type(sy.Integer('12345'))
<class 'sympy.core.numbers.Integer'>
>>> sy.Float(1.2345)
1.23450000000000
>>> sy.Float('1.2345')
1.23450000000000
>>> type(sy.Float('1.2345'))
<class 'sympy.core.numbers.Float'>
>>> sy.Rational(1, 2)
1/2
>>> sy.Integer(1) / sy.Integer(3)
1/3
>>> sy.Rational(1, 2) + sy.Rational(1, 3)
5/6
>>> 1 + 2 * sy.I
1 + 2*I
>>> 1.1 + 2.2 * sy.I
1.1 + 2.2*I
>>> sy.sqrt(2)
sqrt(2)
>>> sy.sqrt(4)
2
>>> sy.sqrt(8)
2*sqrt(2)
>>> sy.pi
pi
>>> sy.E
E
>>> sy.oo
oo
- 数式の出力
- init_printing() を実行すると、使用しているコンソールに適した方法で数式を表示する
- SymPy は LaTex のフォーマットで数式を出力することができる
- それを受け付けるコンソール (たとえば IPython QTConsole など) であれば、美しい数式が表示される
- 本家の SymPy Live で公開されている Online Shell を試してみるとよい
- そうでなければ unicode pretty printer が使用される
- init_printing() の引数に use_unicode=False を指定すると ascii pretty printer になる
- 関数 latex() は数式を Latex 形式で出力する
- Latex 形式の数式は JavaScript のライブラリ MathJax を使うと Web 上で表示できる
- MathJax は拙作のページ お気楽 MathJax 超入門 を参照
>>> sy.init_printing() >>> sy.sqrt(2) √2 >>> 1 / sy.sqrt(2) √2 ── 2 >>> sy.pi π >>> sy.init_printing(use_unicode=False) >>> ssy.sqrt(2) ___ \/ 2 >>>s1 / sy.sqrt(2) ___ \/ 2 ----- 2 >>> sy.pi pi
- Latex 形式の出力例と MathJax での表示
>>> sy.latex(sy.sqrt(2))
\sqrt{2}
>>> sy.latex(1/sy.sqrt(2))
\frac{\sqrt{2}}{2}
>>> sy.latex(sy.pi)
\pi
\(\begin{array}{l}
\sqrt{2} \\
\frac{\sqrt{2}}{2} \\
\pi
\end{array}\)
- 変数の定義
- SumPy の場合、「シンボル (symbol)」を使って数式の変数を表す
- プログラミングにおいて、シンボルというデータ型は「記号」を意味するのが一般的
- Lisp / Scheme の世界では、シンボルは基本的なデータ型のひとつ
- シンボルは Symbol(), symbols(), var() などで生成する
- 引数にはシンボルの名前 (文字列) を渡す
- Symbol('name') => symbol
- symbols('name1 name2 ... nameN') => symbol1, symbol2, ..., symbolN
- var('name1 name2 ... nameN') => symbol1, symbol2, ..., symbolN
- Symbol() はシンボルをひとつ生成する
- symbols() と var() は複数のシンボルを生成する
- 引数の文字列を空白文字やカンマ (,) で区切る
- コロン (:) を使うと複数のシンボルを簡単に指定できる
- たとえば、a:z とすると a から z までの 26 個のシンボルを生成する
- x:10 は x0 から x9 まで, x1:6 は x1 から x5 までのシンボルを生成する
- 生成したシンボルは Python の変数に格納して使用する
- シンボル名と Python の変数名は同じにしたほうがわかりやすい
- var() は同じ名前の大域変数に生成したシンボルを格納する
>>> x, y, z = sy.symbols('x y z')
>>> x
x
>>> y
y
>>> z
z
>>> x + 2*y + 3*z
x + 2⋅y + 3⋅z
>>> (x + y) ** 2
2
(x + y)
>>> (x + y + z) ** 3
3
(x + y + z)
>>> x**3 + 2*x**2 + 3*x + 4
3 2
x + 2⋅x + 3⋅x + 4
>>> sy.sqrt(x)
√x
>>> sy.sqrt(x*x + y*y)
_________
╱ 2 2
╲╱ x + y
>>> sy.var('a:c')
(a, b, c)
>>> a
a
>>> b
b
>>> c
c
>>> sy.var('x1:4')
(x₁, x₂, x₃)
>>> x1
x₁
>>> x2
x₂
>>> x3
x₃
- 数式の展開と因数分解
- 数式 expr の展開は関数 expand() で、因数分解は関数 factor() で行うことができる
- 数式の展開は目的別の関数も用意されている
- expand_power_exp(), expand_power_base(), 指数を含む式の展開
- expand_trig(), 三角関数を含む式の展開
- expand_log(), 対数関数を含む式の展開
- この他にもいろいろある
- 詳細はリファレンス Simplify を参照
>>> sy.expand((x + y)**2)
2 2
x + 2⋅x⋅y + y
>>> sy.expand((x + y + z)**2)
2 2 2
x + 2⋅x⋅y + 2⋅x⋅z + y + 2⋅y⋅z + z
>>> sy.expand((x + y)**3)
3 2 2 3
x + 3⋅x ⋅y + 3⋅x⋅y + y
>>> a = sy.expand((x + y)**4)
>>> a
4 3 2 2 3 4
x + 4⋅x ⋅y + 6⋅x ⋅y + 4⋅x⋅y + y
>>> sy.factor(a)
4
(x + y)
>>> sy.factor(x**2 - 1)
(x - 1)⋅(x + 1)
>>> sy.factor(x**2 - 2*x + 1)
2
(x - 1)
>>> sy.factor(x**3 + y**3)
⎛ 2 2⎞
(x + y)⋅⎝x - x⋅y + y ⎠
>>> sy.expand_power_exp(x**(y+z))
y z
x ⋅x
>>> (x*y)**z
z
(x⋅y)
>>> sy.expand_power_base((x*y)**z)
z
(x⋅y)
>>> sy.expand_power_base((x*y)**z, force=True)
z z
x ⋅y
>>> sy.expand_trig(sy.sin(x + y))
sin(x)⋅cos(y) + sin(y)⋅cos(x)
>>> sy.expand_trig(sy.cos(x + y))
-sin(x)⋅sin(y) + cos(x)⋅cos(y)
>>> sy.expand_trig(sy.sin(2*x))
2⋅sin(x)⋅cos(x)
>>> sy.expand_trig(sy.cos(2*x))
2
2⋅cos (x) - 1
>>> sy.expand_log(sy.log(x*y))
log(x⋅y)
>>> sy.expand_log(sy.log(x*y), force=True)
log(x) + log(y)
>>> sy.expand_log(sy.log(x/y))
⎛x⎞
log⎜─⎟
⎝y⎠
>>> sy.expand_log(sy.log(x/y), force=True)
log(x) - log(y)
>>> sy.expand_log(sy.log(x**2))
⎛ 2⎞
log⎝x ⎠
>>> sy.expand_log(sy.log(x**2), force=True)
2⋅log(x)
>>> sy.var('x1 y1 z1', positive=True)
(x₁, y₁, z₁)
>>> sy.expand_log(sy.log(x1*y1))
log(x₁) + log(y₁)
>>> sy.expand_log(sy.log(x1/y1))
log(x₁) - log(y₁)
>>> sy.expand_log(sy.log(x1**2))
2⋅log(x₁)
- 数式を展開できない場合は、引数の数式をそのまま返す
- たとえば、log(x) の定義域は x > 0 だが、変数 x の範囲が負数を含んでいると数式を展開できない
- シンボルを生成するとき、positive=True を指定すると、その変数がとりうる値は正数に限定される
- または、force=True を指定すると、強制的に式を展開することができる
- 数式の簡約化
- 数式の簡約化は関数 simplify() を使うと簡単
- 目的別の関数も用意されている
- powsimp(), 指数の簡約化
- trigsimp(), 三角関数を含む式の簡約化
- logcombine(), 対数関数を含む式の簡約化
- この他にもいろいろある
- 詳細はリファレンス Simplify を参照
>>> (x**2 + 2*x + 1)/(x + 1) 2 x + 2⋅x + 1 ──────────── x + 1 >>> sy.simplify((x**2 + 2*x + 1)/(x + 1)) x + 1 >>> sy.simplify((x**2 - 1)/(x + 1)) x - 1 >>> x**y * x**z y z x ⋅x >>> sy.powsimp(x**y * x**z) y + z x >>> x**y / x**z y -z x ⋅x >>> sy.powsimp(x**y / x**z) y - z x >>> sy.sin(x)**2 + sy.cos(x)**2 2 2 sin (x) + cos (x) >>> sy.trigsimp(sy.sin(x)**2 + sy.cos(x)**2) 1 >>> sy.sin(x)*sy.cos(y) + sy.cos(x)*sy.sin(y) sin(x)⋅cos(y) + sin(y)⋅cos(x) >>> sy.trigsimp(sy.sin(x)*sy.cos(y) + sy.cos(x)*sy.sin(y)) sin(x + y) >>> sy.cos(x)*sy.cos(y) + sy.sin(x)*sy.sin(y) sin(x)⋅sin(y) + cos(x)⋅cos(y) >>> sy.trigsimp(sy.cos(x)*sy.cos(y) + sy.sin(x)*sy.sin(y)) cos(x - y) >>> 1 + sy.tan(x)**2 2 tan (x) + 1 >>> sy.trigsimp(1 + sy.tan(x)**2) 1 ─────── 2 cos (x) >>> sy.log(x) + sy.log(y) log(x) + log(y) >>> sy.logcombine(sy.log(x) + sy.log(y)) log(x) + log(y) >>> sy.logcombine(sy.log(x) + sy.log(y), force=True) log(x⋅y) >>> sy.log(x) - sy.log(y) log(x) - log(y) >>> sy.logcombine(sy.log(x) - sy.log(y)) log(x) - log(y) >>> sy.logcombine(sy.log(x) - sy.log(y), force=True) ⎛x⎞ log⎜─⎟ ⎝y⎠ >>> x * sy.log(y) x⋅log(y) >>> sy.logcombine(x * sy.log(y)) x⋅log(y) >>> sy.logcombine(x * sy.log(y), force=True) ⎛ x⎞ log⎝y ⎠
- 数式の評価
- 数式 expr の変数に値を代入するにはメソッド subs() を使う
expr.subs(変数, 値) => 値 or 数式
expr.subs([(変数1, 値1), (変数2, 値2), ...]) => 値 or 数式
expr.subs({変数1: 値1, 変数2: 値2, ...}) => 値 or 数式
expr.evalf([n]) => float_number sympy.N(expr, [n]) => float_number
>>> a = x**2
>>> a
2
x
>>> a.subs(x, 10)
100
>>> a.subs(x, 1.2345)
1.52399025000000
>>> a.subs(x, y + z)
2
(y + z)
>>> a.subs(x, sy.sqrt(2))
2
>>> b = a.subs(x, y + z)
>>> b.subs({y: sy.sqrt(2), z: sy.sqrt(3)})
2
(√2 + √3)
>>> sy.pi.evalf()
3.14159265358979
>>> sy.N(sy.pi, 50)
3.1415926535897932384626433832795028841971693993751
>>> sy.sqrt(2).evalf(50)
1.4142135623730950488016887242096980785696718753769
>>> b.subs({y: sy.sqrt(2), z: sy.sqrt(3)}).evalf()
9.89897948556636
>>> b.subs({y: sy.sqrt(2), z: sy.sqrt(3)}).evalf(20)
9.8989794855663561964
●多項式
- 多項式の除算で商と余りを求めるには関数 div() を使う
- 有理式 (多項式の分数) の簡約化には関数 cansel() がある
- 関数 apart() は有理式を「部分分数」に分解する
- 部分分数は、分母が因数分解されている有理式をいくつかの有理式に分解すること
- 次の条件を満たすとき、有理式 g(x) / f(x) は簡単な形に分解できる
- f(x) は 1 次式の積に因数分解できるような整式であること
- g(x) は f(x) より次数が少ない整式であること
\( \dfrac{g(x)}{f(x)} = \dfrac{b_1}{x - a_1} + \dfrac{b_2}{x - a_2} + \cdots + \dfrac{b_n}{x - a_n} \) - 関数 collect() は指定した変数で式をまとめる
- そのあと、メソッド coeff() で指定した次数の係数を取り出すことができる
>>> sy.div(x**3 + x**2 - 4*x + 1, x - 2)
⎛ 2 ⎞
⎝x + 3⋅x + 2, 5⎠
>>> sy.div(x**3 - x**2 - 4*x + 4, x - 2)
⎛ 2 ⎞
⎝x + x - 2, 0⎠
>>> (x**3 - x**2 - 4*x + 4) / (x - 2)
3 2
x - x - 4⋅x + 4
─────────────────
x - 2
>>> sy.cancel((x**3 - x**2 - 4*x + 4) / (x - 2))
2
x + x - 2
>>> sy.cancel((x**2 + 2*x + 1) / (x**2 + x))
x + 1
─────
x
>>> 1/(x - 1) + 1/(x - 2)
1 1
───── + ─────
x - 1 x - 2
>>> sy.cancel(1/(x - 1) + 1/(x - 2))
2⋅x - 3
──────────────
2
x - 3⋅x + 2
>>> sy.apart((2*x - 3)/(x**2 - 3*x + 2))
1 1
───── + ─────
x - 1 x - 2
>>> sy.apart((6*x**2 + x - 17) / (x**3 - 7*x -6))
1 3 2
───── + ───── + ─────
x + 2 x + 1 x - 3
>>> sy.apart((x + 1) / (x**4 + x**2))
x + 1 1 1
- ───── + ─── + ────
2 x 2
x + 1 x
>>> x**2 + y*x + z*x + y*z
2
x + x⋅y + x⋅z + y⋅z
>>> sy.collect(x**2 + y*x + z*x + y*z, x)
2
x + x⋅(y + z) + y⋅z
>>> sy.collect(x**2 + y*x + z*x + y*z, x).coeff(x, 2)
1
>>> sy.collect(x**2 + y*x + z*x + y*z, x).coeff(x, 1)
y + z
>>> sy.collect(x**2 + y*x + z*x + y*z, x).coeff(x, 0)
y⋅z
- 方程式の求解には関数 solveset(expr, var) を使う
- 数式 expr が 0 になる変数 var の値を求める
- キーワード引数 domain で領域を指定できる (Complexes が default)
- たとえば、x2 + 1 = 0 の解は I, -I になるが、実数では存在しない
- 解が存在しない場合は空集合を表す EmptySet() を返す
- SymPy の集合 (Set) は Python の set とは違う (あとで説明する)
- SymPy には特別な集合を表すクラスがあらかじめ定義されている
- EmptySet, 空集合
- UniversalSet, 全体集合
- Naturals, 自然数全体の集合
- Naturals0, 零と自然数全体の集合
- Integers, 整数全体の集合
- Reals, 実数全体の集合
- Complexes, 複素数全体の集合
- これらのクラスのオブジェクト (シングルトン) は sympy.S の同名の変数に格納されている
- 関数 roots(expr, var) は解とその個数を辞書に格納して返す
- 重根があるときは便利
>>> sy.solveset(x**2 - 1, x)
{-1, 1}
>>> sy.solveset(x**2 + 1, x)
{-ⅈ, ⅈ}
>>> sy.S.UniversalSet
UniversalSet()
>>> sy.S.EmptySet
∅
>>> sy.S.Complexes
ℂ
>>> sy.S.Reals
ℝ
>>> sy.S.Integers
ℤ
>>> sy.S.Naturals
ℕ
>>> sy.solveset(x**2 + 1, x, domain=sy.Reals)
∅
>>> sy.var('a b c')
(a, b, c)
>>> sy.solveset(a*x**2 + b*x + c, x)
⎧ _____________ _____________ ⎫
⎪ ╱ 2 ╱ 2 ⎪
⎨ b ╲╱ -4⋅a⋅c + b b ╲╱ -4⋅a⋅c + b ⎬
⎪- ──── - ────────────────, - ──── + ────────────────⎪
⎩ 2⋅a 2⋅a 2⋅a 2⋅a ⎭
>>> sy.solveset(x**3, x)
{0}
>>> sy.roots(x**3, x)
{0: 3}
>>> sy.solveset(x**3 - 4*x**2 + 5*x - 2, x)
{1, 2}
>>> sy.roots(x**3 - 4*x**2 + 5*x - 2, x)
{1: 2, 2: 1}
- 連立一次方程式は関数 linsolve([expr1, expr2, ...], [var1, var2, ...]) を使って解く
- 式と変数はタプルに格納して渡してもよい
- 鶴亀算
- 鶴と亀、合わせて 100 匹いる。足の合計が 272 本のとき、鶴と亀はそれぞれ何匹ずついるか。
- 鶴と亀とトンボが合わせて 10 匹いる。足の合計が 38 本で羽の合計が 14 枚であるとき、鶴と亀とトンボはそれぞれ何匹ずついるか。(トンボの足は 6 本で羽は 4 枚)
- 鶏と犬とタコ、合わせて 24 匹が台所にいる。足の合計が 102 本のとき、鶏、犬、タコはそれぞれ何匹ずついるか。
- 解答
- x + y = 100, 2x + 4y = 272 を解く
- x + y + z = 10, 2x + 4y + 6z = 38, 2x + 4z = 14 を解く
- x + y + z= 24, 2x + 4y + 8z = 102 を解く
- solveset() や linsolve() の他にも、方程式の解を求める関数 solve() がある
>>> sy.linsolve([x + y - 100, 2*x + 4*y - 272], [x, y])
{(64, 36)}
>>> sy.linsolve([x + y + z - 10, 2*x + 4*y + 6*z - 38, 2*x + 4*z -14], [x, y, z])
{(3, 5, 2)}
>>> sy.linsolve([x + y + z - 24, 2*x + 4*y + 8*z - 102], [x, y, z])
{(2⋅z - 3, -3⋅z + 27, z)}
●微積分
- 微分
- 微分は関数 diff(expr, var, [n]) で行う
- 引数 n に数値を指定すると高階微分になる
- または、diff(expr, var, var, ...) のように変数 var の後に同じ変数を指定すると高階微分になる
- 多変数関数の微分 (偏微分) も diff(expr, var1, var2, ...) で OK
- Derivative() は diff() と引数が同じで、評価前の状態を保持するオブジェクトを返す
- メソッド doit() で微分を実行する
>>> sy.var('n x y z')
(n, x, y, z)
>>> sy.diff(x**2, x)
2⋅x
>>> sy.diff(x**2, x, 2)
2
>>> sy.diff(x**2, x, 3)
0
>>> sy.diff(x**n, x)
n
n⋅x
────
x
>>> sy.diff(x**n, x, 2)
n
n⋅x ⋅(n - 1)
────────────
2
x
>>> sy.diff(sy.log(x), x)
1
─
x
>>> sy.diff(sy.exp(x), x)
x
ℯ
>>> sy.diff(sy.sin(x), x)
cos(x)
>>> sy.diff(sy.cos(x), x)
-sin(x)
>>> sy.diff(sy.tan(x), x)
2
tan (x) + 1
>>> sy.diff(x**3*y**3*z**3, x)
2 3 3
3⋅x ⋅y ⋅z
>>> sy.diff(x**3*y**3*z**3, x, x)
3 3
6⋅x⋅y ⋅z
>>> sy.diff(x**3*y**3*z**3, x, x, y, y, z, z)
216⋅x⋅y⋅z
>>> sy.diff(x**3*y**3*z**3, x, 2, y, 2, z, 2)
216⋅x⋅y⋅z
>>> sy.Derivative((x**3 * y**3 * z**3), x, y, z)
3
∂ ⎛ 3 3 3⎞
───────────⎝x ⋅y ⋅z ⎠
∂z ∂y ∂x
>>> sy.Derivative((x**3 * y**3 * z**3), x, y, z).doit()
2 2 2
27⋅x ⋅y ⋅z
>>> sy.Derivative((x**3 * y**3 * z**3), x, 2, y, 2, z, 2)
6
∂ ⎛ 3 3 3⎞
───────────⎝x ⋅y ⋅z ⎠
2 2 2
∂z ∂y ∂x
>>> sy.Derivative((x**3 * y**3 * z**3), x, 2, y, 2, z, 2).doit()
216⋅x⋅y⋅z
- 積分は関数 integrate(expr, var) で行う (積分定数は出力されない)
- 定積分も integrate(expr, (var, low, high)) で OK
- 二重積分も integrate(expr, (var1, l1, h1), (var2, l2, h2), ...) で OK
- Integral() は integrate() と引数が同じで、評価前の状態を保持するオブジェクトを返す
- メソッド doit() で積分を実行する
- 積分を評価できないときは Integral() を返す
>>> sy.integrate(x, x) 2 x ── 2 >>> sy.integrate(x**2, x) 3 x ── 3 >>> sy.integrate(x**3, x) 4 x ── 4 >>> sy.integrate(x, (x, 0, 1)) 1/2 >>> sy.integrate(x**2, (x, 0, 1)) 1/3 >>> sy.integrate(x**3, (x, 0, 1)) 1/4 >>> sy.integrate(sy.exp(x), x) x ℯ >>> sy.integrate(sy.exp(-x), x) -x -ℯ >>> sy.integrate(sy.exp(-x), (x, 0, sy.oo)) 1 >>> sy.integrate(1/x, x) log(x) >>> sy.integrate(sy.log(x), x) x⋅log(x) - x >>> sy.integrate(sy.sin(x), x) -cos(x) >>> sy.integrate(sy.cos(x), x) sin(x) >>> sy.integrate(sy.tan(x), x) -log(cos(x)) >>> sy.integrate(4/(1 + x**2), x) 4⋅atan(x) >>> sy.integrate(4/(1 + x**2), (x, 0, 1)) π >>> sy.Integral(x*y**2, x, y) ⌠ ⌠ ⎮ ⎮ 2 ⎮ ⎮ x⋅y dx dy ⌡ ⌡ >>> sy.Integral(x*y**2, x, y).doit() 2 3 x ⋅y ───── 6 >>> sy.integrate(x*y**2, (x, 0, 1), (y, 0, 1)) 1/6 >>> sy.integrate(x*y**2, (x, 1 - y, 1), (y, 0, 1)) 3/20 >>> sy.integrate(x**x, x) ⌠ ⎮ x ⎮ x dx ⌡
- 極限は関数 limit(function, var, point) で計算する
- f(x) の x -> 0 の極限は limit(f(x), x, 0) とする
- 極限の方向は第 4 引数で指定する ('+' or '-')
>>> sy.limit(x, x, sy.oo) ∞ >>> sy.limit(1/x, x, sy.oo) 0 >>> sy.limit(1/x, x, 0, '+') ∞ >>> sy.limit(1/x, x, 0, '-') -∞ >>> sy.limit(x/(x + 1), x, sy.oo) 1 >>> sy.limit(sy.sin(x)/x, x, 0) 1 >>> sy.limit(sy.sqrt(x**2+3*x+4) - x, x, sy.oo) 3/2
- メソッド series() は関数 f(x) をテーラー展開する
f(x).series(var, [x0, n])
>>> sy.cos(x).series(x)
2 4
x x ⎛ 6⎞
1 - ── + ── + O⎝x ⎠
2 24
>>> sy.sin(x).series(x)
3 5
x x ⎛ 6⎞
x - ── + ──── + O⎝x ⎠
6 120
>>> sy.exp(x).series(x)
2 3 4 5
x x x x ⎛ 6⎞
1 + x + ── + ── + ── + ──── + O⎝x ⎠
2 6 24 120
>>> sy.exp(x).series(x, 0, 10)
2 3 4 5 6 7 8 9
x x x x x x x x ⎛ 10⎞
1 + x + ── + ── + ── + ──── + ──── + ───── + ───── + ────── + O⎝x ⎠
2 6 24 120 720 5040 40320 362880
>>> sy.exp(x).series(x).removeO()
5 4 3 2
x x x x
──── + ── + ── + ─ + x + 1
120 24 6 2
●集合
- Python には集合を表すデータ型 set があるが、SymPy ではクラス Set を使う
- SymPy の Set は immutable なデータ構造
- Set は基本クラスで、実際に使用するのはサブクラス
- ここでは集合の基本的な使い方を簡単に説明する
- 詳細はリファレンス Sets を参照
- 基本的な演算子とメソッド
- 和集合, +, |, union
- 積集合, &, intersect, intersection
- 差集合, -, complement (a - b は b.complement(a) と同じ)
- 対称差, ^, symmetric_difference ((a - b) | (b - a) と同じ)
- 直積集合, *, (a * b は ProductSet(a, b) と同じ)
- a ** n は a * a * ... * a (n 個の a の直積集合)
- べき集合, powerset
- 部分集合の判定, issubset, is_subset, issuperset, is_superset
- 真部分集合の判定, is_proper_subset, is_proper_superset
- 積集合 (共通集合) の有無, isdisjoint, is_disjoint
- 要素 x は集合 a に含まれているか, x.contains(a), x in a
- EmptySet は空集合を表すクラス (シングルトンは sympy.S.EmptySet)
- 属性 is_EmptySet は True (他のクラスのオブジェクトは None)
- 属性 is_iterable は False
- 関数 len() の値は 0
- UniversalSet は全体集合を表すクラス (シングルトンは sympy.S.UniversalSet)
- 属性 is_UniversalSet は True (他のクラスのオブジェクトは None)
- 属性 is_iterable は False
- 関数 len() は適用不可
>>> import sympy as sy >>> sy.init_printing() >>> sy.S.EmptySet ∅ >>> sy.S.EmptySet.is_EmptySet True >>> sy.S.EmptySet.is_iterable False >>> len(sy.S.EmptySet) 0 >>> sy.S.UniversalSet UniversalSet() >>> sy.S.UniversalSet.is_UniversalSet True >>> sy.S.UniversalSet.is_iterable False >>> sy.S.UniversalSet | sy.S.EmptySet UniversalSet() >>> sy.S.UniversalSet & sy.S.EmptySet ∅
- Interval は実数区間を表すクラス
Interval(s, e, left_open=False, right_open=False) => [s, e]
- 返り値は Interval のオブジェクトだが、表示には角カッコや丸カッコが用いられる
- キーワード引数 xxxx_open で xxxx 側の open / close を指定する
- (s, e), s < x < e
- [s, e), s <= x < e
- (s, e], s < x <= e
- [s, e], s <= x <= e
- または次のクラスメソッドを使う
- Ropen(s, e) => [s, e)
- Lopen(s, e) => (s, e]
- open(s, e) => (s, e)
- 端点 s, e の open / close はメソッド left_open, right_open で確認できる
- 端点 s, e には oo, -oo を指定できる
- 属性 is_iterable は False
- 関数 len() は適用不可
>>> a = sy.Interval(1, 10) >>> a [1, 10] >>> a.is_iterable False >>> 1 in a True >>> 0 in a False >>> 10 in a True >>> 11 in a False >>> b = sy.Interval(5, 15) >>> b [5, 15] >>> a & b [5, 10] >>> a | b [1, 15] >>> a - b [1, 5) >>> b - a (10, 15] >>> a ^ b [1, 5) ∪ (10, 15] >>> 5 in a ^ b False >>> 1 in a ^ b True >>> 10 in a ^ b False >>> 15 in a ^ b True
- FiniteSet は有限個の要素を持つ集合を表すクラス
FiniteSet(item1, item2, ..., itemN) => {item1, item2., ..., itemN}
- Python の frozenset (immutable な set) とほぼ同じ
- 返り値は FiniteSet のオブジェクトだが、表示には { ... } が用いられる
- 属性 is_iterable は True (イテレータが利用できる)
- 関数 len() は要素数を返す
>>> a = sy.FiniteSet(1, 2, 3, 4)
>>> a
{1, 2, 3, 4}
>>> a.is_iterable
True
>>> for x in a: print(x)
...
1
2
3
4
>>> len(a)
4
>>> for x in range(0, 6):
... print(x, x in a)
...
0 False
1 True
2 True
3 True
4 True
5 False
>>> b = sy.FiniteSet(3, 4, 5, 6)
>>> b
{3, 4, 5, 6}
>>> a | b
{1, 2, 3, 4, 5, 6}
>>> a & b
{3, 4}
>>> a - b
{1, 2}
>>> b - a
{5, 6}
>>> a ^ b
{1, 2, 5, 6}
- 集合演算を表すクラス
- Union, 和集合
- Intersection. 積集合
- Complement, 差集合
- SymmetricDifference, 対称差
- ProductSet, 直積集合
>>> c = sy.Interval(5, 8)
>>> c
[5, 8]
>>> a | c
{1, 2, 3, 4} ∪ [5, 8]
>>> b | c
{3, 4} ∪ [5, 8]
>>> a & c
∅
>>> b & c
{5, 6}
>>> a - c
{1, 2, 3, 4}
>>> c - a
[5, 8]
>>> b - c
{3, 4}
>>> c - b
(5, 6) ∪ (6, 8]
>>> a ^ c
{1, 2, 3, 4} ∪ [5, 8]
>>> b ^ c
{3, 4} ∪ (5, 6) ∪ (6, 8]
>>> a * b
{1, 2, 3, 4} × {3, 4, 5, 6}
>>> for x in a * b: print(x)
...
(1, 3)
(1, 4)
(1, 5)
(1, 6)
(2, 3)
(2, 4)
(2, 5)
(2, 6)
(3, 3)
(3, 4)
(3, 5)
(3, 6)
(4, 3)
(4, 4)
(4, 5)
(4, 6)
>>> a * c
{1, 2, 3, 4} × [5, 8]
>>> (1, 5.5) in a * c
True
>>> (4, 8.1) in a * c
False
>>> (2.5, 6) in a * c
False
- 特別な集合を表すクラス
- Naturals, 自然数全体の集合
- Naturals0, 零と自然数全体の集合
- Integers, 整数全体の集合
- Reals, 実数全体の集合
- Complexes, 複素数全体の集合
- Range, Python の range() とよく似た集合
- インデックスによるアクセスが可能
- oo や -oo の指定もできる
- ImageSet, 写像
- ImageSet(func, xs) は集合 xs の要素に関数 func を適用した集合を表す
- 第 1 引数 func には SymPy の Lambda() を渡す
- Lambda() は Python の lambda 式とよく似ている
Lambda(x, expr) は lambda x: expr のこと Lambda((x, y, z, ...), expr) は lambda x, y, z, ...: expr のこと
>>> c & sy.S.Naturals
{5, 6, 7, 8}
>>> c | sy.S.Naturals
ℕ ∪ [5, 8]
>>> sy.Reals - c
(-∞, 5) ∪ (8, ∞)
>>> sy.Integers - c
ℤ \ [5, 8]
>>> 5 in sy.Integers - c
False
>>> 5.5 in sy.Integers - c
False
>>> 6 in sy.Integers - c
False
>>> 7 in sy.Integers - c
False
>>> 8 in sy.Integers - c
False
>>> 9 in sy.Integers - c
True
>>> sy.Range(1, 5)
{1, 2, 3, 4}
>>> sy.Range(1, 8, 2)
{1, 3, 5, 7}
>>> d = sy.Range(1, sy.oo)
>>> d
{1, 2, …, ∞}
>>> d[0]
1
>>> d[1]
2
>>> d[100]
101
>>> d[-1]
∞
>>> sy.var('x y z')
(x, y, z)
>>> a = sy.ImageSet(sy.Lambda(x, x * x), sy.S.Naturals0)
>>> a
⎧ 2 │ ⎫
⎨x │ x ∊ ℕ₀⎬
⎩ │ ⎭
>>> 100 in a
True
>>> 200 in a
False
>>> 400 in a
True
>>> b = sy.ImageSet(sy.Lambda(x, x * x), sy.Range(10))
>>> b
⎧ 2 │ ⎫
⎨x │ x ∊ {0, 1, …, 9}⎬
⎩ │ ⎭
>>> for n in b: print(n)
...
0
1
4
9
16
25
36
49
64
81