●行列
- 行列の生成
- SymPy の行列は mutable, 数値だけではなく記号も格納することができる
- SymPy の行列 (Matrix) は Matrix() で生成する
Matrix([x1, x2, ..., xn]) => n 行 1 列 (列ベクトル) Matrix([[x1, x2, ..., xn]]) => 1 行 n 列 (行ベクトル) Matrix([[x11, x12, ... x1n], ..., [xm1, xm2, ..., xmn]]) => m 行 n 列 Matrix(m, n, [x1, ... ]) => m 行 n 列 Matrix(m, n, function) => m 行 n 列
A.shape => (m, n)
>>> sy.Matrix([1, 2, 3]) ⎡1⎤ ⎢ ⎥ ⎢2⎥ ⎢ ⎥ ⎣3⎦ >>> sy.Matrix([[1, 2, 3]]) [1 2 3] >>> sy.Matrix([[1, 2], [3, 4]]) ⎡1 2⎤ ⎢ ⎥ ⎣3 4⎦ >>> sy.Matrix(3, 3, range(1, 10)) ⎡1 2 3⎤ ⎢ ⎥ ⎢4 5 6⎥ ⎢ ⎥ ⎣7 8 9⎦ >>> sy.Matrix(3, 3, lambda i, j: i * 3 + j) ⎡0 1 2⎤ ⎢ ⎥ ⎢3 4 5⎥ ⎢ ⎥ ⎣6 7 8⎦ >>> sy.zeros(2) ⎡0 0⎤ ⎢ ⎥ ⎣0 0⎦ >>> sy.zeros(2, 3) ⎡0 0 0⎤ ⎢ ⎥ ⎣0 0 0⎦ >>> sy.ones(2) ⎡1 1⎤ ⎢ ⎥ ⎣1 1⎦ >>> sy.ones(2, 3) ⎡1 1 1⎤ ⎢ ⎥ ⎣1 1 1⎦ >>> sy.eye(2) ⎡1 0⎤ ⎢ ⎥ ⎣0 1⎦ >>> sy.eye(2, 3) ⎡1 0 0⎤ ⎢ ⎥ ⎣0 1 0⎦ >>> sy.eye(3, 2) ⎡1 0⎤ ⎢ ⎥ ⎢0 1⎥ ⎢ ⎥ ⎣0 0⎦ >>> sy.diag(sy.eye(2), sy.ones(2)) ⎡1 0 0 0⎤ ⎢ ⎥ ⎢0 1 0 0⎥ ⎢ ⎥ ⎢0 0 1 1⎥ ⎢ ⎥ ⎣0 0 1 1⎦ >>> sy.diag(sy.Matrix([[1, 2, 3]]), sy.Matrix([4, 5, 6])) ⎡1 2 3 0⎤ ⎢ ⎥ ⎢0 0 0 4⎥ ⎢ ⎥ ⎢0 0 0 5⎥ ⎢ ⎥ ⎣0 0 0 6⎦
- 行列のアクセス
- 行列 A の要素 (i, j) は A[i, j] でアクセスする
- A[k] は行列を平坦化した配列の k 番目の要素にアクセスする
- メソッド row(i) は i 行目を、メソッド col(i) は i 列目を取り出す
- スライス操作もできる
- NumPy と違い、row(), col(), スライス操作は行列の要素をコピーする
>>> x = sy.Matrix(4, 4, range(16)) >>> x ⎡0 1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 7 ⎥ ⎢ ⎥ ⎢8 9 10 11⎥ ⎢ ⎥ ⎣12 13 14 15⎦ >>> x[0, 0] 0 >>> x[3, 3] 15 >>> x.row(0) [0 1 2 3] >>> x.row(3) [12 13 14 15] >>> x.col(1) ⎡1 ⎤ ⎢ ⎥ ⎢5 ⎥ ⎢ ⎥ ⎢9 ⎥ ⎢ ⎥ ⎣13⎦ >>> x.col(2) ⎡2 ⎤ ⎢ ⎥ ⎢6 ⎥ ⎢ ⎥ ⎢10⎥ ⎢ ⎥ ⎣14⎦ >>> x[1, :] [4 5 6 7] >>> x[:, 2] ⎡2 ⎤ ⎢ ⎥ ⎢6 ⎥ ⎢ ⎥ ⎢10⎥ ⎢ ⎥ ⎣14⎦ >>> x[2:, 2:] ⎡10 11⎤ ⎢ ⎥ ⎣14 15⎦ >>> x[2:, 2:] = sy.Matrix(2, 2, [100, 100, 100, 100]) >>> x ⎡0 1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 7 ⎥ ⎢ ⎥ ⎢8 9 100 100⎥ ⎢ ⎥ ⎣12 13 100 100⎦ >>> y = x[:2, :2] >>> y ⎡0 1⎤ ⎢ ⎥ ⎣4 5⎦ >>> y[1,1] *= 10 >>> y ⎡0 1 ⎤ ⎢ ⎥ ⎣4 50⎦ >>> x ⎡0 1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 7 ⎥ ⎢ ⎥ ⎢8 9 100 100⎥ ⎢ ⎥ ⎣12 13 100 100⎦ >>> z = x.row(0) >>> z [0 1 2 3] >>> z[3] *= 10 >>> z [0 1 2 30] >>> x ⎡0 1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 7 ⎥ ⎢ ⎥ ⎢8 9 100 100⎥ ⎢ ⎥ ⎣12 13 100 100⎦
- 基本的な演算処理
- 行列 M, N の足し算 M + N, 引き算 M - N
- 行列 M, N の積 M * N, (NumPy のような要素同士の積ではない)
- 要素同士の積はメソッド M.multiply_elementwise(N) を使う
- 行列 M とスカラー n の乗算 n * M, M * n, 除算 M / n, べき乗 M**n
- 行列 M の転置行列は M.T
- ベクトル v1, v2 の内積はメソッド v1.dot(v2)
- M.applyfunc(function) は行列 M の要素に関数 function を適用する
>>> x = sy.Matrix([[1, 2, 3], [4, 5, 6]]) >>> y = x * 10 >>> y ⎡10 20 30⎤ ⎢ ⎥ ⎣40 50 60⎦ >>> y / 5 ⎡2 4 6 ⎤ ⎢ ⎥ ⎣8 10 12⎦ >>> x + y ⎡11 22 33⎤ ⎢ ⎥ ⎣44 55 66⎦ >>> y - x ⎡9 18 27⎤ ⎢ ⎥ ⎣36 45 54⎦ >>> x * y.T ⎡140 320⎤ ⎢ ⎥ ⎣320 770⎦ >>> x.multiply_elementwise(y) ⎡10 40 90 ⎤ ⎢ ⎥ ⎣160 250 360⎦ >>> z = sy.Matrix([[1, 1], [1, 0]]) >>> z ** 2 ⎡2 1⎤ ⎢ ⎥ ⎣1 1⎦ >>> z ** 10 ⎡89 55⎤ ⎢ ⎥ ⎣55 34⎦ >>> z ** 40 ⎡165580141 102334155⎤ ⎢ ⎥ ⎣102334155 63245986 ⎦ >>> z ** 100 ⎡573147844013817084101 354224848179261915075⎤ ⎢ ⎥ ⎣354224848179261915075 218922995834555169026⎦ >>> x = sy.Matrix([1, 2, 3]) >>> y = sy.Matrix([4, 5, 6]) >>> x ⎡1⎤ ⎢ ⎥ ⎢2⎥ ⎢ ⎥ ⎣3⎦ >>> y ⎡4⎤ ⎢ ⎥ ⎢5⎥ ⎢ ⎥ ⎣6⎦ >>> x.T [1 2 3] >>> x.T * y [32] >>> x.dot(y) 32 >>> sy.Matrix([[1, 2], [3, 4]]).applyfunc(sy.sqrt) ⎡1 √2⎤ ⎢ ⎥ ⎣√3 2 ⎦ >>> sy.Matrix([[1, 2], [3, 4]]).applyfunc(lambda x: x**2) ⎡1 4 ⎤ ⎢ ⎥ ⎣9 16⎦
- 行列の基本的な操作
- 連結
- xs.row_join(ys), 行方向
- xs.col_join(ys), 列方向
- 挿入
- xs.row_insert(i, ys), i 行目に行ベクトル ys を挿入
- xs.col_insert(i, ys), i 列目に列ベクトル ys を挿入
- 削除
- xs.row_del(i), i 行目を削除
- xs.col_del(i), i 列目を削除
- これらのメソッドは行列 xs を破壊的に修正する
>>> x = sy.Matrix([[1,2,3],[4,5,6],[7,8,9]]) >>> x ⎡1 2 3⎤ ⎢ ⎥ ⎢4 5 6⎥ ⎢ ⎥ ⎣7 8 9⎦ >>> x.row_join(sy.ones(3)) ⎡1 2 3 1 1 1⎤ ⎢ ⎥ ⎢4 5 6 1 1 1⎥ ⎢ ⎥ ⎣7 8 9 1 1 1⎦ >>> x.col_join(sy.ones(3)) ⎡1 2 3⎤ ⎢ ⎥ ⎢4 5 6⎥ ⎢ ⎥ ⎢7 8 9⎥ ⎢ ⎥ ⎢1 1 1⎥ ⎢ ⎥ ⎢1 1 1⎥ ⎢ ⎥ ⎣1 1 1⎦ >>> x.row_insert(0, sy.Matrix([[10, 11, 12]])) ⎡10 11 12⎤ ⎢ ⎥ ⎢1 2 3 ⎥ ⎢ ⎥ ⎢4 5 6 ⎥ ⎢ ⎥ ⎣7 8 9 ⎦ >>> x.row_insert(3, sy.Matrix([[10, 11, 12]])) ⎡1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 ⎥ ⎢ ⎥ ⎢7 8 9 ⎥ ⎢ ⎥ ⎣10 11 12⎦ >>> x.row_insert(0, sy.Matrix([[10, 11, 12]])) ⎡10 11 12⎤ ⎢ ⎥ ⎢1 2 3 ⎥ ⎢ ⎥ ⎢4 5 6 ⎥ ⎢ ⎥ ⎣7 8 9 ⎦ >>> x.row_insert(3, sy.Matrix([[10, 11, 12]])) ⎡1 2 3 ⎤ ⎢ ⎥ ⎢4 5 6 ⎥ ⎢ ⎥ ⎢7 8 9 ⎥ ⎢ ⎥ ⎣10 11 12⎦ >>> x.col_insert(0, sy.Matrix([10, 11, 12])) ⎡10 1 2 3⎤ ⎢ ⎥ ⎢11 4 5 6⎥ ⎢ ⎥ ⎣12 7 8 9⎦ >>> x.col_insert(3, sy.Matrix([10, 11, 12])) ⎡1 2 3 10⎤ ⎢ ⎥ ⎢4 5 6 11⎥ ⎢ ⎥ ⎣7 8 9 12⎦ >>> x.row_del(0) >>> x ⎡4 5 6⎤ ⎢ ⎥ ⎣7 8 9⎦ >>> x.col_del(2) >>> x ⎡4 5⎤ ⎢ ⎥ ⎣7 8⎦
●線形代数
- メソッド V.norm() はベクトル V のノルム (大きさ) を求める
- 行列 A のトレース (trace, 跡) は A.trace()
- トレースは行列の対角線上にある要素の和のこと (\(a_{11} + a_{22} + \cdots + a_{nn}\))
- 行列 A の逆行列 A-1 は A.inv() または A**(-1) で、行列式は A.det() で求めることができる
- 行列 A のランク (rank) は A.rank()
- 連立一次方程式 Ax = b を解く場合、拡大係数行列 (A, b) を関数 linsolve() に渡すこともできる
>>> sy.Matrix([1,2,3,4,5]).norm()
√55
>>> sy.Matrix([[1,2,3,4,5]]).norm()
√55
>>> sy.var('a b c d')
(a, b, c, d)
>>> x = sy.Matrix([[a, b], [c, d]])
>>> x
⎡a b⎤
⎢ ⎥
⎣c d⎦
>>> x.trace()
a + d
>>> x**(-1)
⎡ d -b ⎤
⎢───────── ─────────⎥
⎢a⋅d - b⋅c a⋅d - b⋅c⎥
⎢ ⎥
⎢ -c a ⎥
⎢───────── ─────────⎥
⎣a⋅d - b⋅c a⋅d - b⋅c⎦
>>> x.inv()
⎡ d -b ⎤
⎢───────── ─────────⎥
⎢a⋅d - b⋅c a⋅d - b⋅c⎥
⎢ ⎥
⎢ -c a ⎥
⎢───────── ─────────⎥
⎣a⋅d - b⋅c a⋅d - b⋅c⎦
>>> x.det()
a⋅d - b⋅c
>>> sy.Matrix(3, 3, range(1, 10))
⎡1 2 3⎤
⎢ ⎥
⎢4 5 6⎥
⎢ ⎥
⎣7 8 9⎦
>>> sy.Matrix(3, 3, range(1, 10)).trace()
15
>>> sy.Matrix(3, 3, range(1, 10)).det()
0
>>> sy.Matrix(3, 3, range(1, 10)).rank()
2
>>> sy.Matrix(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 10])
⎡1 2 3 ⎤
⎢ ⎥
⎢4 5 6 ⎥
⎢ ⎥
⎣7 8 10⎦
>>> sy.Matrix(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 10]).det()
-3
>>> sy.Matrix(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 10]).rank()
3
>>> sy.Matrix(3, 3, [1, 2, 3, 4, 5, 6, 7, 8, 10]).inv()
⎡-2/3 -4/3 1 ⎤
⎢ ⎥
⎢-2/3 11/3 -2⎥
⎢ ⎥
⎣ 1 -2 1 ⎦
- 鶴亀算
- 鶴と亀、合わせて 100 匹いる。足の合計が 272 本のとき、鶴と亀はそれぞれ何匹ずついるか。
- 鶴と亀とトンボが合わせて 10 匹いる。足の合計が 38 本で羽の合計が 14 枚であるとき、鶴と亀とトンボはそれぞれ何匹ずついるか。(トンボの足は 6 本で羽は 4 枚)
- 鶏と犬とタコ、合わせて 24 匹が台所にいる。足の合計が 102 本のとき、鶏、犬、タコはそれぞれ何匹ずついるか。
- 解答
- x + y = 100, 2x + 4y = 272 を解く
- x + y + z = 10, 2x + 4y + 6z = 38, 2x + 4z = 14 を解く
- x + y + z= 24, 2x + 4y + 8z = 102 を解く
>>> sy.linsolve((sy.Matrix([[1, 1], [2, 4]]), sy.Matrix([100, 272])), (x, y))
{(64, 36)}
>>> sy.linsolve((sy.Matrix([[1, 1, 1], [2, 4, 6], [2, 0, 4]]), sy.Matrix([10, 38, 14])), (x, y, z))
{(3, 5, 2)}
>>> sy.linsolve((sy.Matrix([[1, 1, 1], [2, 4, 8]]), sy.Matrix([24, 102])), (x, y, z))
{(2⋅z - 3, -3⋅z + 27, z)}
- 行列の分解
- 行列 A の LU 分解は LUdecomposition() で, QR 分解は QRdecomposition() で行う
A.LUdecomposition() => (L, U, perm) A.QRdecomposition() => (Q, R)
A.diagonalize() => (P, D)
>>> a = sy.Matrix([[1, 1, 1], [2, 4, 6], [2, 0, 4]]) >>> a ⎡1 1 1⎤ ⎢ ⎥ ⎢2 4 6⎥ ⎢ ⎥ ⎣2 0 4⎦ >>> L, U, _ = a.LUdecomposition() >>> L ⎡1 0 0⎤ ⎢ ⎥ ⎢2 1 0⎥ ⎢ ⎥ ⎣2 -1 1⎦ >>> U ⎡1 1 1⎤ ⎢ ⎥ ⎢0 2 4⎥ ⎢ ⎥ ⎣0 0 6⎦ >>> L * U ⎡1 1 1⎤ ⎢ ⎥ ⎢2 4 6⎥ ⎢ ⎥ ⎣2 0 4⎦ >>> Q, R = a.QRdecomposition() >>> Q ⎡ -2⋅√2⎤ ⎢1/3 0 ─────⎥ ⎢ 3 ⎥ ⎢ ⎥ ⎢ √2 √2 ⎥ ⎢2/3 ─── ─── ⎥ ⎢ 2 6 ⎥ ⎢ ⎥ ⎢ -√2 √2 ⎥ ⎢2/3 ─── ─── ⎥ ⎣ 2 6 ⎦ >>> R ⎡3 3 7 ⎤ ⎢ ⎥ ⎢0 2⋅√2 √2 ⎥ ⎢ ⎥ ⎣0 0 √2 ⎦ >>> Q * R ⎡1 1 1⎤ ⎢ ⎥ ⎢2 4 6⎥ ⎢ ⎥ ⎣2 0 4⎦ >>> b = sy.Matrix([[0, 2, 4], [1, 1, 1], [4, 2, 6]]) >>> b ⎡0 2 4⎤ ⎢ ⎥ ⎢1 1 1⎥ ⎢ ⎥ ⎣4 2 6⎦ >>> L, U, p = b.LUdecomposition() >>> L ⎡1 0 0⎤ ⎢ ⎥ ⎢0 1 0⎥ ⎢ ⎥ ⎣4 -1 1⎦ >>> U ⎡1 1 1⎤ ⎢ ⎥ ⎢0 2 4⎥ ⎢ ⎥ ⎣0 0 6⎦ >>> p [[0, 1]] >>> L * U ⎡1 1 1⎤ ⎢ ⎥ ⎢0 2 4⎥ ⎢ ⎥ ⎣4 2 6⎦ >>> Q, R = b.QRdecomposition() >>> Q ⎡ √34 √2 ⎤ ⎢ 0 ──── ──── ⎥ ⎢ 6 6 ⎥ ⎢ ⎥ ⎢ √17 2⋅√34 -2⋅√2 ⎥ ⎢ ─── ───── ───── ⎥ ⎢ 17 51 3 ⎥ ⎢ ⎥ ⎢4⋅√17 -√34 √2 ⎥ ⎢───── ───── ──── ⎥ ⎣ 17 102 6 ⎦ >>> R ⎡ 9⋅√17 25⋅√17 ⎤ ⎢√17 ────── ──────⎥ ⎢ 17 17 ⎥ ⎢ ⎥ ⎢ 6⋅√34 11⋅√34 ⎥ ⎢ 0 ────── ──────⎥ ⎢ 17 17 ⎥ ⎢ ⎥ ⎣ 0 0 √2 ⎦ >>> Q * R ⎡0 2 4⎤ ⎢ ⎥ ⎢1 1 1⎥ ⎢ ⎥ ⎣4 2 6⎦ >>> P, D = a.diagonalize() >>> P ⎡-3 -1 1⎤ ⎢ ⎥ ⎢-2 -2 4⎥ ⎢ ⎥ ⎣2 1 1⎦ >>> D ⎡1 0 0⎤ ⎢ ⎥ ⎢0 2 0⎥ ⎢ ⎥ ⎣0 0 6⎦ >>> P * D * P.inv() ⎡1 1 1⎤ ⎢ ⎥ ⎢2 4 6⎥ ⎢ ⎥ ⎣2 0 4⎦
- 固有値と固有ベクトル
- メソッド eigenvals() は行列の固有値を、eigenvects() は固有ベクトルを求める
- 固有値と固有ベクトルの説明は拙作のページ NumPy 入門: 固有値と固有ベクトル を参照
>>> a = sy.Matrix([[1, 2], [2, 1]])
>>> a
⎡1 2⎤
⎢ ⎥
⎣2 1⎦
>>> a.eigenvals()
{-1: 1, 3: 1}
>>> a.eigenvects()
⎡⎛ ⎡⎡-1⎤⎤⎞ ⎛ ⎡⎡1⎤⎤⎞⎤
⎢⎜-1, 1, ⎢⎢ ⎥⎥⎟, ⎜3, 1, ⎢⎢ ⎥⎥⎟⎥
⎣⎝ ⎣⎣1 ⎦⎦⎠ ⎝ ⎣⎣1⎦⎦⎠⎦
>>> b = sy.ones(3) + sy.diag(3,3,3)
>>> b
⎡4 1 1⎤
⎢ ⎥
⎢1 4 1⎥
⎢ ⎥
⎣1 1 4⎦
>>> b.eigenvals()
{3: 2, 6: 1}
>>> b.eigenvects()
⎡⎛ ⎡⎡-1⎤ ⎡-1⎤⎤⎞ ⎛ ⎡⎡1⎤⎤⎞⎤
⎢⎜ ⎢⎢ ⎥ ⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎢⎜3, 2, ⎢⎢1 ⎥, ⎢0 ⎥⎥⎟, ⎜6, 1, ⎢⎢1⎥⎥⎟⎥
⎢⎜ ⎢⎢ ⎥ ⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎣⎝ ⎣⎣0 ⎦ ⎣1 ⎦⎦⎠ ⎝ ⎣⎣1⎦⎦⎠⎦
>>> c = sy.diag(1,2,3,4,5)
>>> c
⎡1 0 0 0 0⎤
⎢ ⎥
⎢0 2 0 0 0⎥
⎢ ⎥
⎢0 0 3 0 0⎥
⎢ ⎥
⎢0 0 0 4 0⎥
⎢ ⎥
⎣0 0 0 0 5⎦
>>> c.eigenvals()
{1: 1, 2: 1, 3: 1, 4: 1, 5: 1}
>>> c.eigenvects()
⎡⎛ ⎡⎡1⎤⎤⎞ ⎛ ⎡⎡0⎤⎤⎞ ⎛ ⎡⎡0⎤⎤⎞ ⎛ ⎡⎡0⎤⎤⎞ ⎛ ⎡⎡0⎤⎤⎞⎤
⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎢⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟⎥
⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎢⎜1, 1, ⎢⎢0⎥⎥⎟, ⎜2, 1, ⎢⎢0⎥⎥⎟, ⎜3, 1, ⎢⎢1⎥⎥⎟, ⎜4, 1, ⎢⎢0⎥⎥⎟, ⎜5, 1, ⎢⎢0⎥⎥⎟⎥
⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎢⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟ ⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢0⎥⎥⎟⎥
⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟⎥
⎣⎝ ⎣⎣0⎦⎦⎠ ⎝ ⎣⎣0⎦⎦⎠ ⎝ ⎣⎣0⎦⎦⎠ ⎝ ⎣⎣0⎦⎦⎠ ⎝ ⎣⎣1⎦⎦⎠⎦
●素数と約数
- gcd(m, n), 最大公約数
- lcm(m, n), 最小公倍数
- divisors(n), 約数をリストに格納して返す
- キーワード引数 generator=True とするとジェネレータを返す
- divisor_count(n), 約数の個数を返す
- factorint(n), 素因数分解 (素因数がキーで指数が値の辞書を返す)
- primefactor(n), 素因数のみをリストに格納して返す
- prime(i), i 番目の素数を返す (1 から数える)
- primepi(n), n 以下の素数の個数を返す
- nextprime(n, ith=1), n から ith 番目の素数を求める
- prevprime(n), n 以下で最大の素数を求める
- primerange(a, b), a 以上 b 未満の素数を生成するジェネレータを返す
- primorial(n), 素数階乗 (1 番目から n 番目までの素数の積)
- isprime(n), 素数の判定
- multiplicity(p, m), pn == m となる整数 n を求める (p は素数)
>>> sy.gcd(12345678, 123456789)
9
>>> sy.gcd(1234321, 12345654321)
121
>>> sy.lcm(5, 7)
35
>>> sy.lcm(14, 35)
70
>>> sy.divisors(24)
[1, 2, 3, 4, 6, 8, 12, 24]
>>> sy.divisors(12345678)
[1, 2, 3, 6, 9, 18, 47, 94, 141, 282, 423, 846, 14593, 29186, 43779, 87558, 131337, 262674,
685871, 1371742, 2057613, 4115226, 6172839, 12345678]
>>> sy.divisors(123456789)
[1, 3, 9, 3607, 3803, 10821, 11409, 32463, 34227, 13717421, 41152263, 123456789]
>>> sy.divisors(1111111111)
[1, 11, 41, 271, 451, 2981, 9091, 11111, 100001, 122221, 372731, 2463661, 4100041, 27100271,
101010101, 1111111111]
>>> sy.divisor_count(24)
8
>>> sy.divisor_count(12345678)
24
>>> sy.divisor_count(123456789)
12
>>> sy.divisor_count(1111111111)
16
>>> sy.factorint(24)
{2: 3, 3: 1}
>>> sy.factorint(12345678)
{2: 1, 3: 2, 47: 1, 14593: 1}
>>> sy.factorint(123456789)
{3: 2, 3607: 1, 3803: 1}
>>> sy.factorint(1111111111)
{11: 1, 41: 1, 271: 1, 9091: 1}
>>> sy.primefactors(24)
[2, 3]
>>> sy.primefactors(12345678)
[2, 3, 47, 14593]
>>> sy.primefactors(123456789)
[3, 3607, 3803]
>>> sy.primefactors(1111111111)
[11, 41, 271, 9091]
>>> for i in range(1, 11): print(sy.prime(i))
...
2
3
5
7
11
13
17
19
23
29
>>> sy.primepi(29)
10
>>> sy.primepi(100)
25
>>> sy.nextprime(100)
101
>>> sy.nextprime(100, ith=2)
103
>>> sy.prevprime(100)
97
>>> list(sy.primerange(100, 200))
[101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199]
>>> list(sy.primerange(100, 199))
[101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197]
>>> sy.primorial(3)
30
>>> sy.primorial(6)
30030
>>> sy.isprime(199)
True
>>> sy.isprime(1991)
False
>>> sy.isprime(19991)
True
>>> sy.multiplicity(2, 256)
8
>>> sy.multiplicity(2, 257)
0
>>> sy.multiplicity(3, 27)
3
>>> sy.multiplicity(3, 28)
0
- 簡単な問題
- 3,000,000 以下の素数の個数とその最大値を求めてください。
- 3,000,001 を素因数分解してください。素因数分解とは、素数でない整数 (合成数) を素数の積の形に書き表すことです。たとえば、12 は 22 * 3 と素因数分解することができます。
- 3,000,000 以下のフィボナッチ素数 (フィボナッチ数で素数) の個数とその最大値を求めてください。
- 差が 2 である素数の組を「双子素数 (twin prime)」といいます。3,000,000 以下の双子素数の個数とその最大値を求めてください。
- 2n - 1 (n は自然数) の形の自然数を「メルセンヌ数 (Mersenne number)」といい、素数であるメルセンヌ数を「メルセンヌ素数」といいます。n が 32 以下の条件でメルセンヌ素数を求めてください。
- 完全数(かんぜんすう,perfect number)とは、その数自身を除く約数の和が、その数自身と等しい自然数のことです。10000 以下の完全数を求めてください。
- 友愛数(ゆうあいすう)とは、異なる 2 つの自然数の組で、自分自身を除いた約数の和が、互いに他方と等しくなるような数のことです。100000 以下の友愛数を求めてください。
- 解答1
>>> sy.prevprime(3000000) 2999999 >>> sy.primepi(3000000) 216816
>>> sy.factorint(3000001)
{853: 1, 3517: 1}
- フィボナッチ数は SymPy の関数 fibonacci() で求めることができる
>>> for n in sy.Range(0, sy.oo): ... x = sy.fibonacci(n) ... if x > 3000000: break ... if sy.isprime(x): print(n, x) ... 3 2 4 3 5 5 7 13 11 89 13 233 17 1597 23 28657 29 514229
>>> g = sy.primerange(2, 3000000) >>> c, m, n = 0, 0, 0 >>> p = next(g) >>> for q in g: ... if q - p == 2: ... m, n = p, q ... c += 1 ... p = q ... >>> m 2999831 >>> n 2999833 >>> c 20932
>>> for n in range(2, 33): ... m = 2 ** n - 1 ... if sy.isprime(m): print(n, m) ... 2 3 3 7 5 31 7 127 13 8191 17 131071 19 524287 31 2147483647
- メルセンヌ素数には「リュカ-レーマー・テスト (Lucas-Lehmer primality test)」という高速な素数判定法がある
>>> for x in range(4, 10001): ... if sum(sy.divisors(x)[:-1]) == x: print(x) ... 6 28 496 8128
>>> for x in range(1, 100001): ... m = sum(sy.divisors(x)[:-1]) ... if m < x and x == sum(sy.divisors(m)[:-1]): print(m, x) ... 220 284 1184 1210 2620 2924 5020 5564 6232 6368 10744 10856 12285 14595 17296 18416 66928 66992 67095 71145 63020 76084 69615 87633 79750 88730
●数列と級数
- 数列は sequence() で生成する
sequence(expr, (var, s, e))
- 引数 expr は式または列 (シーケンス)
- sequence() で生成した数列を渡すこともできる
- var は expr で使用する変数 (シンボル) で、s, e はその区間 [s, e] を表す
- expr で使用する変数が一つしかない場合、var を省略することができる
- s は -oo を、e は oo を指定できる
- 区間が有限の場合に限り、生成した数列は iterable になる
- 演算は区間が重なっているところだけ行われる
summation(expr, (var, s, e))
- 引数 expr は数列の一般項 (数列を表す式)
- sequence() で生成した数列 seq の一般項は seq.formula で求めることができる
- var は expr で使用する変数 (シンボル) で、s, e はその区間 [s, e] を表す
- s, e に変数 (シンボル) を指定してもよい
- 次のように、一定の差で並んだ数列を「等差数列」という
- a を「初項」、d を「公差」という
- 等差数列の一般項は次の式で表すことができる
- 初項から an までの和 Sn は次の式で求めることができる
- 公式の導出
- 右辺を逆順に並べ替えて足し算すると、\(2a + (n - 1)d\) が n 個並ぶことになる
- あとは、これを 2 で割り算するだけ
\(a, \ a + d, \ a + 2d, \ a + 3d, \ \cdots, \ a + (n - 1)d, \ \cdots\)
\(a_n = a + (n-1)d\)
\(S_n = \displaystyle \sum_{i=1}^{n} a_i = \frac{n(2a + (n - 1)d)}{2}\)
\(\begin{eqnarray}
S_n &=& a &+& (a + d) &+& \cdots \ &+& (a + (n - 2)d) &+& (a + (n - 1)d)\\
S_n &=& (a + (n - 1)d) &+& (a + (n - 2)d) &+& \cdots \ &+& (a + d) &+& a
\end{eqnarray}\)
足し算すると
\(\begin{array}{l} 2S_n = (2a + (n - 1)d) + (2a + (n - 1)d) + \cdots + (2a + (n - 1)d) + (2a + (n - 1)d) \\ 2S_n = n(2a + (n - 1)d) \\ S_n = \dfrac{n(2a + (n - 1)d)}{2} \end{array}\)
足し算すると
\(\begin{array}{l} 2S_n = (2a + (n - 1)d) + (2a + (n - 1)d) + \cdots + (2a + (n - 1)d) + (2a + (n - 1)d) \\ 2S_n = n(2a + (n - 1)d) \\ S_n = \dfrac{n(2a + (n - 1)d)}{2} \end{array}\)
- 次のように、一定の比で並んだ数列を「等比数列」という
- a を「初項」、d を「公比」という
- 等比数列の一般項は次の式で表すことができる
- 初項から an までの和 Sn は次の式で求めることができる
- 公式の導出
- 右辺を引き算すると \(ar\) から \(ar^{n-1}\) の項がなくなって、\(a - ar^n\) だけになる
- あとは、\(1 - r\) で割り算するだけ
\(a, \ ar, \ ar^2, \ \cdots, \ ar^{n-1}, \ \cdots\)
\(a_n = ar^{n-1}\)
\(S_n = \displaystyle \sum_{i=1}^{n} a_i = \dfrac{a(1 - r^n)}{1 - r}\)
\(
S_n = a + ar + ar^2 + \cdots + ar^{n-1}
\)
両辺を r 倍すると
\( rS_n = ar + ar^2 + \cdots + ar^{n-1} + ar^n \)
これを引き算すると
\(\begin{array}{l} S_n - rS_n = a - ar^n \\ S_n = \dfrac{a(1 - r^n)}{1 - r} \end{array}\)
両辺を r 倍すると
\( rS_n = ar + ar^2 + \cdots + ar^{n-1} + ar^n \)
これを引き算すると
\(\begin{array}{l} S_n - rS_n = a - ar^n \\ S_n = \dfrac{a(1 - r^n)}{1 - r} \end{array}\)
>>> sy.var('m n x y z')
(m, n, x, y, z)
>>> a = sy.sequence(x, (x, 1, 10))
>>> a
[1, 2, 3, 4, …]
>>> list(a)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
>>> a.formula
x
>>> sy.summation(a.formula, (x, 1, 1000))
500500
>>> sy.summation(a.formula, (x, 1, n))
2
n n
── + ──
2 2
>>> b = sy.sequence(2*x+1, (x, 0, 10))
>>> list(b)
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
>>> sy.summation(b.formula, (x, 1, 1000))
1002000
>>> sy.summation(b.formula, (x, 0, n - 1))
2
n
>>> a + b
[4, 7, 10, 13, …]
>>> a - b
[-2, -3, -4, -5, …]
>>> a * b
[3, 10, 21, 36, …]
>>> list(a + b)
[4, 7, 10, 13, 16, 19, 22, 25, 28, 31]
>>> list(a - b)
[-2, -3, -4, -5, -6, -7, -8, -9, -10, -11]
>>> list(a * b)
[3, 10, 21, 36, 55, 78, 105, 136, 171, 210]
>>> b[2]
5
>>> b[3]
7
>>> b.coeff(2)
5
>>> b.coeff(3)
7
>>> b.coeff(2.5)
6.00000000000000
>>> c = sy.sequence(x*x, (x, 1, 10))
>>> c
[1, 4, 9, 16, …]
>>> list(c)
[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
>>> sy.summation(c.formula, (x, 1, 100))
338350
>>> sy.summation(c.formula, (x, 1, n))
3 2
n n n
── + ── + ──
3 2 6
>>> sy.factor(sy.summation(c.formula, (x, 1, n)))
n⋅(n + 1)⋅(2⋅n + 1)
──────────────────
6
>>> d = sy.sequence(x*(x+1), (x, 1, 10))
>>> d
[2, 6, 12, 20, …]
>>> list(d)
[2, 6, 12, 20, 30, 42, 56, 72, 90, 110]
>>> sy.factor(sy.summation(d.formula, (x, 1, n)))
n⋅(n + 1)⋅(n + 2)
─────────────────
3
>>> e = sy.sequence(1/(x*(x+1)), (x, 1, 10))
>>> e
[1/2, 1/6, 1/12, 1/20, …]
>>> list(e)
[1/2, 1/6, 1/12, 1/20, 1/30, 1/42, 1/56, 1/72, 1/90, 1/110]
>>> sy.factor(sy.summation(e.formula, (x, 1, n)))
n
─────
n + 1
>>> f = sy.sequence(2**x, (x, 0, 10))
>>> f
[1, 2, 4, 8, …]
>>> list(f)
[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024]
>>> sy.summation(f.formula, (x, 0, n))
n + 1
2 - 1
>>> sy.summation(y**x, (x, 0, n))
⎧ n + 1 for y = 1
⎪
⎪ n + 1
⎨- y + 1
⎪──────────── otherwise
⎪ -y + 1
⎩
>>> sy.sequence(x + y, (x, 1, 10))
[y + 1, y + 2, y + 3, y + 4, …]
>>> sy.sequence(sy.sequence(x + y, (x, 1, 10)), (y, 11, 20))
[12, 14, 16, 18, …]
>>> list(sy.sequence(sy.sequence(x + y, (x, 1, 10)), (y, 11, 20)))
[12, 14, 16, 18, 20, 22, 24, 26, 28, 30]
>>> list(sy.sequence(sy.sequence(x * y, (x, 1, 10)), (y, 11, 20)))
[11, 24, 39, 56, 75, 96, 119, 144, 171, 200]
- 級数は無限につづく数列の和のこと
- たとえば、等比級数 \(\displaystyle \sum_{n=0}^{\infty} ar^n\) は \(|r| \lt 1\) のとき \(\dfrac{a}{1 - r}\) に収束する
- 級数は summation() の端点 e に oo を指定する
- 調和級数 \(\displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n}\) は発散するが、交代級数 \(\displaystyle \sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n}\) は ln 2 に収束する
>>> sy.summation(x * y ** n, (n, 0, sy.oo)) ⎛⎧ 1 ⎞ ⎜⎪ ──────── for │y│ < 1⎟ ⎜⎪ -y + 1 ⎟ ⎜⎪ ⎟ ⎜⎪ ∞ ⎟ ⎜⎪ ___ ⎟ x⋅⎜⎨ ╲ ⎟ ⎜⎪ ╲ n ⎟ ⎜⎪ ╱ y otherwise ⎟ ⎜⎪ ╱ ⎟ ⎜⎪ ‾‾‾ ⎟ ⎜⎪n = 0 ⎟ ⎝⎩ ⎠ >>> sy.summation(1 / n, (n, 1, sy.oo)) ∞ >>> sy.summation((-1)**(n+1) / n, (n, 1, sy.oo)) log(2)
- 多角数 (polygonal number)
- 点を多角形の形に並べたとき、その総数を多角数 (polygonal number) という
- 三角形に配置したものを三角数 (triangular number)
- 四角形に配置したものを四角数 (square number)
- 五角形に配置したものを五角数 (pentagonal number)
- 三角数は公差 1、四角数は公差 2、五角数は公差 3、p 角数は公差 p - 2 の等差数列の和になる
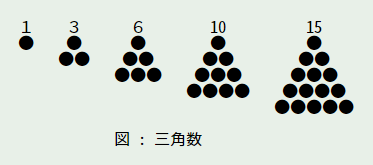
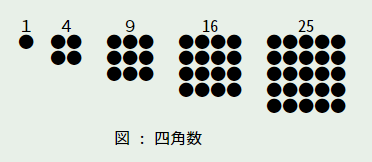
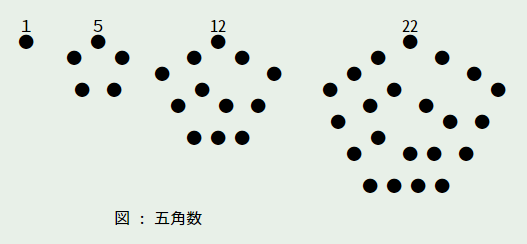
n 三角数 四角数 五角数
---+-----------------------------------------------------------
1 | 1 1 1
2 | 3 = 1+2 4 = 1+3 5 = 1+4
3 | 6 = 1+2+3 9 = 1+3+5 12 = 1+4+7
4 | 10 = 1+2+3+4 16 = 1+3+5+7 22 = 1+4+7+10
5 | 15 = 1+2+3+4+5 25 = 1+3+5+7+9 35 = 1+4+7+10+13
6 | 21 = 1+2+3+4+5+6 36 = 1+3+5+7+9+11 51 = 1+4+7+10+13+16
・・・・・・ ・・・・・・・ ・・・・・
n | n(n + 1) / 2 n^2 n(3n - 1) / 2
>>> sy.var('m n x y z')
(m, n, x, y, z)
>>> sy.init_printing()
>>> sy.factor(sy.summation((m - 2)*(x - 1) + 1, (x, 1, n)))
n⋅(m⋅n - m - 2⋅n + 4)
──────────────────────
2
>>> sy.factor(sy.summation((m - 2)*(x - 1) + 1, (x, 1, n))).subs(m, 3)
n⋅(n + 1)
──────────
2
>>> sy.factor(sy.summation((m - 2)*(x - 1) + 1, (x, 1, n))).subs(m, 4)
2
n
>>> sy.factor(sy.summation((m - 2)*(x - 1) + 1, (x, 1, n))).subs(m, 5)
n⋅(3⋅n - 1)
────────────
2
- 三角数を 1 から順番に足した数列を考えることができる
- これを三角錐数 (triangular pyramidal number) という
- 同様に、四角錐数 (square pyramidal number) と五角錐数 (pentagonal pyramidal number) がある
>>> sy.factor(sy.summation(x*(x + 1)/2, (x, 1, n)))
n⋅(n + 1)⋅(n + 2)
──────────────────
6
>>> sy.summation(x*(x + 1)/2, (x, 1, n)).subs(n, 1000000)
166667166667000000
>>> sy.factor(sy.summation(x**2, (x, 1, n)))
n⋅(n + 1)⋅(2⋅n + 1)
────────────────────
6
>>> sy.summation(x**2, (x, 1, n)).subs(n, 1000000)
333333833333500000
>>> sy.factor(sy.summation(x*(3*x - 1)/2, (x, 1, n)))
2
n ⋅(n + 1)
──────────
2
>>> sy.summation(x*(3*x - 1)/2, (x, 1, n)).subs(n, 1000000)
500000500000000000