整数の論理演算とビット操作
今回はC言語のビット操作について説明します。
●ビット演算子
C言語のビット演算子を下表に示します。
| 演算子 | 操作 |
|---|---|
| x & y | ビットごとの論理積 |
| x | y | ビットごとの論理和 |
| x ^ y | ビットごとの排他的論理和 |
| ~x | ビットごとの否定 |
| x << y | x を y ビット左シフト |
| x >> y | x を y ビット右シフト |
演算子 & はビットごとの論理積を返します。
5 & 3 => 1
0101
AND 0011
---------
0001
演算子 l はビットごとの論理和を返します。
5 | 3 => 7
0101
OR 0011
--------
0111
演算子 ^ はビットごとの排他的論理和を返します。
5 ^ 3 => 6
0101
XOR 0011
---------
0110
演算子 ~ はビットごとの論理的な否定を返します。
~1 => -2 ~0 => -1
<<, >> はビットをシフトする演算子です。左シフトの場合、下位ビットには 0 が挿入されます。右シフトの場合、正の整数 (または無符号整数) では上位ビットに 0 が挿入されます。負の整数では 1 が挿入されます。これを「算術シフト」といいます。
1 << 8 => 256 1 << 16 => 65536 256 >> 8 => 1 65536 >> 8 => 256 -256 >> 8 => -1
それでは簡単な例題として、基本的なビット操作関数を作ってみましょう。次のリストを見てください。
リスト : 基本的なビット操作 (sample1800.c)
#include <stdio.h>
#include <stdbool.h>
bool test_bit(int x, int n)
{
return x & (1 << n);
}
int set_bit(int x, int n)
{
return x | (1 << n);
}
int clear_bit(int x, int n)
{
return x & ~(1 << n);
}
int main(void)
{
printf("%d\n", test_bit(256, 7));
printf("%d\n", test_bit(256, 8));
printf("%d\n", test_bit(256, 9));
for (int i = 0; i < 8; i++) {
int x = set_bit(0, i);
printf("%d\n", x);
printf("%d\n", clear_bit(x, i));
}
return 0;
}
test_bit は整数 x の n 番目のビットが 1 ならば true を返します。最下位 (LSB) のビットが 0 番目になります。int (32 bit) の場合、n は 0 から 31 になります。1 を n ビット左シフトして、x との論理積が 0 でなければ、n 番目のビットは 1 であることがわかります。
bit_set は x の n 番目のビットを 1 にセットします。1 を n ビット左シフトして、x との論理和を計算すれば、n 番目のビットを 1 にすることができます。clear_bit は x の n 番目のビットを 0 にクリアします。これは n 番目以外のビットを 1 に、n 番目のビットを 0 にして、それと x の論理積を計算すれば、n 番目のビットをクリアすることができます。1 を n ビット左シフトして、その否定を計算すると、n 番目のビット以外は 1 になります。
それでは実際に試してみましょう。
$ clang sample1800.c $ ./a.out 0 1 0 1 0 2 0 4 0 8 0 16 0 32 0 64 0 128 0
●組み合わせの生成
組み合わせの生成は拙作のページ Yet Another Clang Problems で取り上げました。このほかに、n 個の中から m 個を選ぶ組み合わせは、ビットの 0, 1 で表すことができます。たとえば、5 個の数字 (0 - 4) から 3 個を選ぶ場合、数字を 0 番目 から 4 番目のビットに対応させます。すると、1, 3, 4 という組み合わせは 11010 と表すことができます。簡単な例題として、ビットを使って組み合わせを求めてみましょう。
組み合わせを求めるプログラムは次のようになります。
リスト : 組み合わせの生成 (sample1801.c)
#include <stdio.h>
void comb_sub(void (*f)(int), int n, int m, int a)
{
if (m == 0)
f(a);
else if (m == n)
f(a | ((1 << m) - 1));
else {
comb_sub(f, n - 1, m, a);
comb_sub(f, n - 1, m - 1, a | (1 << (n - 1)));
}
}
void combinations(void (*f)(int), int n, int m)
{
comb_sub(f, n, m, 0);
}
void print_comb(int n)
{
printf("%x\n", n);
}
int main(void)
{
combinations(print_comb, 5, 3);
return 0;
}
関数 combinations は n 個の中から m 個を選ぶ組み合わせを生成して、引数の関数 f に渡します。実際の処理は関数 comb_sub で行います。組み合わせは引数 a にセットします。m が 0 になったら、組み合わせがひとつできたので f(a) を呼び出します。n が m と等しくなったならば、残り m 個を全て選びます。(1 << m) - 1 で m 個のビットをオンにして関数 f を呼び出します。
あとは comb_sub を再帰呼び出しします。最初の呼び出しは n 番目の数字を選ばない場合です。n - 1 個の中から m 個を選びます。次の呼び出しが n 番目の数字を選ぶ場合で、a の n - 1 番目のビットをオンにします。そして、n - 1 個の中から m - 1 個を選びます。
それでは 5 個の中から 3 個を選ぶ combinations(5, 3) の実行例を示します。
$ clang sample1801.c $ ./a.out 7 b d e 13 15 16 19 1a 1c
この場合、最小値は 0x07 (111) で最大値は 0x1c (11100) になります。このように、combinations は組み合わせを表す数を昇順で出力します。
●組み合わせに番号を付ける方法
次は、N 通りある組み合わせに 0 から N - 1 までの番号を付ける方法を紹介しましょう。たとえば、6 個の中から 3 個を選ぶ組み合わせは 20 通りありますが、この組み合わせに 0 から 19 までの番号を付けることができます。1 1 1 0 0 0 を例題に考えてみましょう。次の図を見てください。
図 : 6C3 の組み合わせ
最初に 5 をチェックします。5 を選ばない場合は \({}_5 \mathrm{C}_3\) = 10 通りありますね。この組み合わせに 0 から 9 までの番号を割り当てることにすると、5 を選ぶ組み合わせの番号は 10 から 19 までとなります。
次に、4 をチェックします。4 を選ばない場合は、\({}_4 \mathrm{C}_2\) = 6 通りあります。したがって、5 を選んで 4 を選ばない組み合わせに 10 から 15 までの番号を割り当てることにすると、5 と 4 を選ぶ組み合わせには 16 から 19 までの番号となります。
最後に、3 をチェックします。同様に 3 を選ばない場合は 3 通りあるので、これに 16 から 18 までの番号を割り当て、5, 4, 3 を選ぶ組み合わせには 19 を割り当てます。これで組み合わせ 1 1 1 0 0 0 の番号を求めることができました。
では、0 0 0 1 1 1 はどうなるのでしょうか。左から順番にチェックしていくと、最初の 1 が見つかった時点で、その数字を選ばない組み合わせは存在しません。つまり、残りの数字をすべて選ぶしかないわけです。したがって、これが 0 番目となります。
このように、数字を選ぶときに、数字を選ばない場合の組み合わせの数を足し算していけば、その組み合わせの番号を求めることができるのです。
●組み合わせを番号に変換
組み合わせを番号に変換するプログラムは次のようになります。
リスト : 組み合わせを番号に変換
int comb_num(int n, int r)
{
if (n == r || r == 0)
return 1;
else
return comb_num(n, r - 1) * (n - r + 1) / r;
}
// 組み合わせを番号に変換
int comb_to_num_sub(int c, int n, int r, int value)
{
if (r == 0 || n == r)
return value;
else if (test_bit(c, n - 1))
return comb_to_num_sub(c, n - 1, r - 1, value + comb_num(n - 1, r));
else
return comb_to_num_sub(c, n - 1, r, value);
}
int comb_to_num(int c, int n, int r)
{
return comb_to_num_sub(c, n, r, 0);
}
関数 comb_num は組み合わせの数を求めます。comb_to_num の引数 c はビットのオンオフで表した組み合わせ、引数 n と r は \({}_n \mathrm{C}_r\) の n と r を表しています。実際の処理は comb_to_num_sub で行います。引数 value は求める番号を表します。n と r の値が同じになるか、もしくは r が 0 になれば、組み合わせの番号を計算できたので value を返します。
そうでない場合、c の n - 1 ビットの値を調べます。ビットがオンであれば、value に comb_num(n - 1, r) の値を足し算し、r を -1 して comb_to_num_sub を再帰呼び出しします。そうでなければ、value と r の値はそのままで comb_to_num_sub を再帰呼び出しします。
●番号を組み合わせに変換
逆に、番号から組み合わせを求めるプログラムも簡単に作ることができます。次のリストを見てください。
リスト : 番号を組み合わせに変換
// 番号を組み合わせに変換
int num_to_comb_sub(int value, int n, int r, int c)
{
if (r == 0)
return c;
else if (n == r)
return c | ((1 << n) - 1);
else {
int k = comb_num(n - 1, r);
if (value >= k)
return num_to_comb_sub(value - k, n - 1, r - 1, set_bit(c, n - 1));
else
return num_to_comb_sub(value, n - 1, r, c);
}
}
int num_to_comb(int value, int n, int r)
{
return num_to_comb_sub(value, n, r, 0);
}
引数 value が番号で、引数 n と r は \({}_n \mathrm{C}_r\) の n と r を表しています。実際の処理は num_to_comb_sub で行います。引数 c が求める組み合わせです。たとえば、n = 5, r = 3 の場合、ビットが 1 になるのは \({}_4 \mathrm{C}_2\) = 6 通りあり、0 になるのは \({}_4 \mathrm{C}_3\) = 4 通りあります。したがって、数値が 0 - 3 の場合はビットを 0 にし、4 - 9 の場合はビットを 1 にすればいいわけです。
ビットを 0 にした場合、残りは \({}_4 \mathrm{C}_3\) = 4 通りになるので、同様に次のビットを決定します。ビットを 1 にした場合、残りは \({}_4 \mathrm{C}_2\) = 6 通りになるので、value から 4 を引いて numToComb を再帰呼び出しして次のビットを決定します。
r が 0 の場合は、組み合わせが完成したので c を返します。n と r が等しい場合は、残りのビットをすべて 1 にセットしてから c を返します。それ以外の場合は、\({}_{n-1} \mathrm{C}_r\) の値を comb_num(n - 1, r) で求めて変数 k にセットします。value が k 以上であれば変数 c のビットを 1 にセットし、value から k を引き算して num_to_comb_sub を再帰呼び出しします。そうでなければ、num_to_comb_sub を再帰呼び出しするだけです。
それでは、n = 5, r = 3 の場合の実行例を示します。
リスト : 簡単なテスト (sample1802.c)
int main(void)
{
for (int i = 0; i < 10; i++) {
int a = num_to_comb(i, 5, 3);
printf("%d -> %d -> %d\n", i, a, comb_to_num(a, 5, 3));
}
return 0;
}
$ clang sample1802.c $ ./a.out 0 -> 7 -> 0 1 -> 11 -> 1 2 -> 13 -> 2 3 -> 14 -> 3 4 -> 19 -> 4 5 -> 21 -> 5 6 -> 22 -> 6 7 -> 25 -> 7 8 -> 26 -> 8 9 -> 28 -> 9
正常に動作していますね。この方法を使うと、n 個ある組み合わせの中の i 番目 (0 <= i < n) の組み合わせを簡単に求めることができます。
●ちょっと便利なビット操作
最も右側 (LSB 側) にある 1 を 0 にクリアする、逆に最も右側にある 0 を 1 にセットすることは簡単にできます。
(1) 右側にある 1 をクリア => x & (- x) x : 1 1 1 1 x - 1 : 1 1 1 0 ---------------- AND : 1 1 1 0 x : 1 0 0 0 x - 1 : 0 1 1 1 ---------------- AND : 0 0 0 0 (2) 右側にある 0 を 1 にセット => x | (x + 1) x : 0 0 0 0 x + 1 : 0 0 0 1 ---------------- OR : 0 0 0 1 x : 0 1 1 1 x - 1 : 1 0 0 0 ---------------- OR : 1 1 1 1
上図 (1) を見てください。x から 1 を引くと、右側から連続している 0 は桁借りにより 1 になり、最初に出現する 1 が 0 になります。したがって、x & (x - 1) を計算すると、最も右側にある 1 を 0 にクリアすることができます。(2) の場合、x に 1 を足すと、右側から連続している 1 は桁上がりにより 0 になり、最初に出現する 0 が 1 になります。x | (x + 1) を計算すれば、最も右側にある 0 を 1 にセットすることができます。
また、最も右側にある 1 を取り出すことも簡単にできます。簡単な例として 4 ビットの整数値を考えてみます。負の整数を 2 の補数で表した場合、4 ビットで表される整数は -8 から 7 になります。次の図を見てください。
0 : 0000
1 : 0001 -1 : 1111 1 & (-1) => 0001
2 : 0010 -2 : 1110 2 & (-2) => 0010
3 : 0011 -3 : 1101 3 & (-3) => 0001
4 : 0100 -4 : 1100 4 & (-4) => 0100
5 : 0101 -5 : 1011 5 & (-5) => 0001
6 : 0110 -6 : 1010 6 & (-6) => 0010
7 : 0111 -7 : 1001 7 & (-7) => 0001
-8 : 1000
図 : 最も右側にある 1 を取り出す方法
2 の補数はビットを反転した値 (1 の補数) に 1 を加算することで求めることができます。したがって、x と -x の論理積 x & (-x) は、最も右側にある 1 だけが残り、あとのビットはすべて 0 になります。
●ビットが 1 の個数を求める
次は、ビットが 1 の個数を数える処理を作ってみましょう。データ型を Int とすると、プログラムは次のようになります。
リスト : ビットカウント
int bit_count(unsigned int n)
{
int c = 0;
unsigned int m = n;
while (m != 0) {
m &= m - 1;
c++;
}
return c;
}
整数 n の右側から順番に 1 をクリアしていき、0 になるまでの回数を求めます。とても簡単ですね。32 個のビットを順番に調べるよりも高速です。
int を 32 bit とする場合、次の方法で 1 の個数をもっと高速に求めることができます。
リスト : ビットカウント (2)
int bit_count1(unsigned int n)
{
unsigned int a = (n & 0x55555555) + ((n >> 1) & 0x55555555);
unsigned int b = (a & 0x33333333) + ((a >> 2) & 0x33333333);
unsigned int c = (b & 0x0f0f0f0f) + ((b >> 4) & 0x0f0f0f0f);
unsigned int d = (c & 0x00ff00ff) + ((c >> 8) & 0x00ff00ff);
return (d & 0xffff) + (d >> 16);
}
最初に、整数を 2 bit ずつに分割して、1 の個数を求めます。たとえば、整数 n を 4 bit で考えてみましょう。5 を 2 進数で表すと 0101 になり、n と論理積を計算すると 0, 2 番目のビットが 1 であれば、結果の 0, 2 番目のビットは 1 になります。同様に n を 1 ビット右シフトして論理積を計算すると、1, 3 番目のビットが 1 であれば、結果の 0, 2 番目のビットは 1 になります。あとは、それを足し算すれば 2 bit の中にある 1 の個数を求めることができます。
変数 a には 2 ビットの中の 1 の個数が格納されています。左隣の 2 ビットの値を足し算すれば、4 ビットの中の 1 の個数を求めることができます。次に、左隣の 4 ビットの値を足し算して 8 ビットの中の 1 の個数を求め、左隣の 8 ビットの値を足し算して、というように順番に値を加算していくと 32 ビットの中にある 1 の個数を求めることができます。
bit_count は 1 の個数が多くなると遅くなりますが、bit_count1 は 1 の個数に関係なく高速に動作します。興味のある方は試してみてください。
●参考 URL
ビットが 1 の個数を数える方法は フィンローダさん の 初級C言語Q&A(15) を参考にさせていただきました。フィンローダさんに感謝いたします。
改訂 2023 年 4 月 2 日
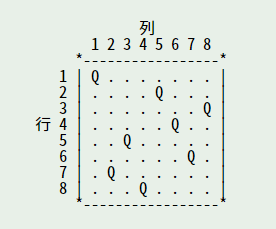 図 : 8 クイーンの解答例
図 : 8 クイーンの解答例
 図 : 斜めの利き筋のチェック
図 : 斜めの利き筋のチェック