1月30日
●プログラミング言語のインストール
今回は SBCL (Common Lisp) と Ruby をインストールして、たらいまわし関数で実行速度を計測しました。Linux 系 OS で SBCL をインストールする場合、パッケージ管理ツールを使ったほうが簡単でしょう。Ubuntu であれば、次のコマンドで SBCL をインストールすることができます。
sudo apt install sbcl
Ubuntu 24.04 (WSL2, Windows11) の場合、SBCL 2.2.9 がインストールされます。
たらいまわし関数とその実行結果を以下に示します。
リスト : たらいまわし関数 (Common Lisp)
(defun tak (x y z)
(if (<= x y)
z
(tak (tak (1- x) y z)
(tak (1- y) z x)
(tak (1- z) x y))))
* (time (tak 22 11 0)) Evaluation took: 3.026 seconds of real time 2.863591 seconds of total run time (2.862462 user, 0.001129 system) 94.65% CPU 7,147,539,961 processor cycles 0 bytes consed 11 * (time (tak 24 12 0)) Evaluation took: 19.459 seconds of real time 18.400291 seconds of total run time (18.400285 user, 0.000006 system) 94.56% CPU 45,927,272,428 processor cycles 0 bytes consed 1
以前のパソコン (Ubuntu 22.04, WSL2, Windows10, Intel Core i5-6200U 2.30GHz) の場合、(tak 22 11 0) は 4.90 秒かかりましたが、今のパソコンでは 3.03 秒ですみました。ところで、Common Lisp の場合、次のように関数単位でデータ型や最適化の指定を行うことができます。
リスト : たらいまわし関数 (Common Lisp, 最適化の指定)
(defun tak (x y z)
(declare (type fixnum x y z)
(optimize (speed 3) (safety 0)))
(if (<= x y)
z
(tak (tak (1- x) y z)
(tak (1- y) z x)
(tak (1- z) x y))))
* (time (tak 22 11 0)) Evaluation took: 0.882 seconds of real time 0.835476 seconds of total run time (0.835476 user, 0.000000 system) 94.67% CPU 2,085,342,053 processor cycles 0 bytes consed 11 * (time (tak 24 12 0)) Evaluation took: 5.727 seconds of real time 5.415333 seconds of total run time (5.415333 user, 0.000000 system) 94.55% CPU 13,516,779,071 processor cycles 0 bytes consed 1
最適化を指定すると、SBCL はC言語にせまる速度を叩き出します。あらためて SBCL の性能はすごいなと感心しました。
Ruby の場合、apt を使ってもいいのですが、少々古いバージョンがインストールされるようです。そこで、今回は snap というツールを使ってみることにしましょう。snap は canonical が開発している新しいパッケージシステムで、Ubuntu 16.04 以降のディストリビューションなら以下のコマンドで ruby をインストールすることができます。
sudo snap install ruby --classic
これで最新 の Ruby (安定板) をインストールすることができます。
$ ruby --version ruby 4.0.0 (2025-12-25 revision 553f1675f3) +PRISM [x86_64-linux]
たらいまわし関数と実行結果を以下に示します。
リスト : たらいまわし関数 (tarai.rb) def tak(x, y, z) return z if x <= y tak(tak(x - 1, y, z), tak(y - 1, z, x), tak(z - 1, x, y)) end
$ irb
irb(main):001> require "benchmark"
=> true
irb(main):002> load "tarai.rb"
=> true
irb(main):003> Benchmark.realtime { tak(22, 11, 0) }
=> 13.76934446999985
前のパソコンの Ruby (ver 3.0.2p107) では 25.59 秒かかりましたが、今のパソコンでは 13.77 秒ですみました。最新の PC ではありませんが、プログラミングを楽しむには十分すぎる性能だと思いました。
1月26日
●新しいパソコン
今まで使っていたパソコン (Windows 10) が壊れたので、新しいノート PC (Windows 11) を買いました。CPU は intel CORE i5-1235U 1.3 GHz、メモリは 8 G byte です。最新のノート PC ではないので、高スペックではありませんが、起動やシャットダウンが今までの PC よりも格段に速くなったのには驚きました。
どのくらい速くなったのか、いつもの「たらいまわし関数」で調べてみました。使用する言語はC言語 (gcc) です。
リスト : たらいまわし関数
#include <stdio.h>
int tak(int x, int y, int z)
{
if (x <= y) {
return z;
} else {
return tak(tak(x - 1, y, z), tak(y - 1, z, x), tak(z - 1, x, y));
}
}
int main(void)
{
printf("%d\n", tak(24, 12, 0));
return 0;
}
$ gcc --version gcc (Ubuntu 11.3.0-1ubuntu1~22.04) 11.3.0 $ gcc -O2 -o takg tak.c $ time ./takg 1 real 0m7.695s user 0m7.694s sys 0m0.000s
- 実行環境 : Ubunts 22.04 LTS (WSL2, Windows 10), Intel Core i5-6200U 2.30GHz
$ gcc --version gcc (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0 $ gcc -O2 -o takg tak.c $ time ./takg 1 real 0m3.851s user 0m3.786s sys 0m0.001s
- 実行環境 : Ubunts 24.04 LTS (WSL2, Windows 11), Intel Core i5-1235U 1.3 GHz
tak(24, 12, 0) で約 2 倍ほど速くなっています。最近の PC は低価格でも高性能ですね。ちなみに、Python3 で tak(22, 11, 0) を計算したところ、62.23 秒から 13.48 秒になりました。これは PC の性能だけではなく、Python3 のバージョンアップ (ver 3.10.12 --> 3.12.3) による実行速度の改善も寄与していると思われます。他の言語でも試してみようと思っています。
1月10日
●Google AI モード
いつもお世話になっている Google に AI モードが導入されました。日本語に対応したのが 2025 年 9 月なので、ご存じの方も多いと思います。AI モードはリンクを羅列するのではなく、AI が回答を直接生成する、という新しい機能です。ようするに、リンク先の Web サイトにいちいちアクセスしなくても、知りたい情報をまとめて得ることができるわけです。もちろん、AI の回答が 100 % 正しいわけではありませんが、このような機能を無料で利用できることに大変驚きました。
たとえば、「プログラミング言語 入門」を AI モードで検索すると、M.Hiroi の環境では冒頭で次のように表示されます。
『2026年現在、プログラミング学習は「AIをどう活用するか」が鍵となっています。初心者が今から始めるのにおすすめの言語と、学習のステップを簡潔に解説します。』
さらに、具体的な言語名を入力すると、その言語の特徴などが表示されます。たとえば Python と入力してみましょう。以下に示す内容が表示されます。
- Pythonで「できること」
- 初心者におすすめの学習ステップ(2026年版)
- おすすめの無料学習サイト
興味のある方は実際に試してみてください。それにしても AI の進歩は速いですね。凄い時代になったものだと驚愕しています。
1月3日
●Google Colaboratory
Google Colaboratory (通称 : Colab) は、Google が提供するブラウザ上で動作する無料の Python 実行環境です。Google アカウントとブラウザ (Chrome など) があれば、すぐに Python のプログラムを実行することができます。
Colab は GPU / TPU を無料で利用できるので、AI やディープラーニングのほうに目が行きがちですが、NumPy, SymPy, matplotlib など便利なライブラリもプリインストールされているので、import するだけで簡単に利用することができます。
なお、Colab の無料版には使用に制限がありますが、それを緩和した有料版も用意されています。学習目的で Colab を利用するのであれば、無料版の機能で十分なように思います。
遅ればせながら、実際に使ってみたところ、とても簡単に利用できることに大変驚きました。たとえば、SymPy で数式を表示してみましょう。次のプログラムを Colab のコードセルで実行します。
> import sympy as sy
sy.init_printing()
x = sy.Symbol('x')
f = x**2 + 2*x + 1
f
Colab の場合、init_printing() を実行すると、数式は MathJax を使って綺麗に表示されます。
グラフを表示することも簡単です。
> f1 = x**2 - 1 sy.plotting.plot(f1, (x, -2, 2))
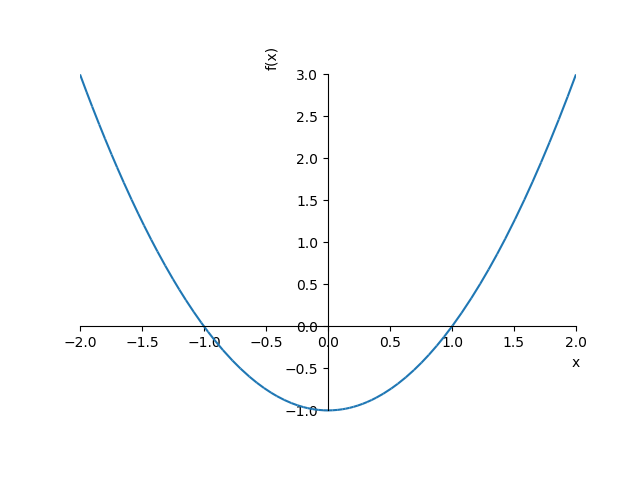
コードや実行結果はノートブックとして Google ドライブに保存され、あとから読み込むことができます。初めて Python を勉強するユーザーにとって、Colab はとても使いやすい実行環境だと思いました。
1月1日
旧年中は大変お世話になりました
本年も M.Hiroi's Home Page をよろしくお願い申し上げます