パズルの説明
今回は皆さんお馴染みの「魔方陣 (Magic square)」を解いてみましょう。それでは問題です。
┌─┬─┬─┐ 式
│A│B│C│ A + B + C = N, A + E + I = N
├─┼─┼─┤ D + E + F = N, C + E + G = N
│D│E│F│ G + H + I = N
├─┼─┼─┤ A + D + G = N
│G│H│I│ B + E + H = N
└─┴─┴─┘ C + F + I = N
図 : 魔方陣
上図の A から I の場所に 1 から 9 までの数字をひとつずつ配置します。縦横斜めの合計が等しくなるように数字を配置してください。
●プログラムの作成
それではプログラムを作りましょう。3 行 3 列の魔方陣は生成検定法で簡単に解くことができます。使用するプログラミング言語は Python3 (ver 3.8.10) です。次のリストを見てください。
リスト : 魔方陣 (3 行 3 列盤)
# 盤面
# 0 1 2
# 3 4 5
# 6 7 8
# 直線を表す配列
lines = [
[0, 1, 2], [3, 4, 5], [6, 7, 8],
[0, 3, 6], [1, 4, 7], [2, 5, 8],
[0, 4, 8], [2, 4, 6]
]
def check(ps):
def add(x, y, z): return ps[x] + ps[y] + ps[z]
xs = [add(*ls) for ls in lines]
return xs.count(xs[0]) == len(xs)
def print_board(ps):
for i in range(9):
print(ps[i], end=' ')
if (i + 1) % 3 == 0: print()
print()
def magic_square(ps = []):
if len(ps) == 9:
if check(ps): print_board(ps)
else:
for n in range(1, 10):
if n not in ps:
ps.append(n)
magic_square(ps)
ps.pop()
関数 magic_square() で 1 から 9 までの数字の順列を生成します。それを関数 check に渡して、魔方陣の条件を満たしているかチェックします。内包表記で各直線の和を求めて、すべて同じ値であれば魔方陣の条件を満たすので True を返します。
メソッド count() は、引数と等しい要素の個数を返します。先頭要素と同じ値が 8 個あれば、すべての要素が等しいことがわかります。条件を満たしていたら print_board() で盤面を表示します。
それでは実行結果を示します。
>>> s = time.time(); magic_square(); print(time.time() - s) 2 7 6 9 5 1 4 3 8 2 9 4 7 5 3 6 1 8 4 3 8 9 5 1 2 7 6 4 9 2 3 5 7 8 1 6 6 1 8 7 5 3 2 9 4 6 7 2 1 5 9 8 3 4 8 1 6 3 5 7 4 9 2 8 3 4 1 5 9 6 7 2 1.665628433227539 実行環境 : Python3 (ver 3.8.10), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
対称解を含めると、解は 8 通りあります。対称解を排除すると枝刈りの効果により、実行時間はもう少し速くなります。
●対称解の排除
対称解のチェックは、下図のように四隅の大小関係を利用すると簡単です。
┌─┬─┬─┐
│A│B│C│
├─┼─┼─┤ A < C < G
│D│E│F│
├─┼─┼─┤ A < I
│G│H│I│
└─┴─┴─┘
図 : 対称解のチェック
魔方陣の場合、回転解が 4 種類あって、鏡像解が 2 種類あります。四隅の大小関係をチェックすることで、これらの対称解を排除することができます。プログラムは次のようになります。
リスト : 重複解の排除
def magic_square1(ps = []):
if len(ps) == 9:
if check(ps): print_board(ps)
else:
for n in range(1, 10):
if n not in ps:
if len(ps) == 2 and ps[0] > n: continue
if len(ps) == 6 and ps[2] > n: continue
if len(ps) == 8 and ps[0] > n: continue
ps.append(n)
magic_square1(ps)
ps.pop()
順列を生成する magic_square1() の中で四隅の大小関係をチェックします。条件を満たしていなければ magic_square1() を再帰呼び出ししません。これで枝刈りを行うことができます。実行結果を示します。
>>> s = time.time(); magic_square1(); print(time.time() - s) 2 9 4 7 5 3 6 1 8 0.3206007480621338
対称解を除くと解は 1 通りしかありません。実行時間も約 5 倍速くなりました。
●五芒星の問題
五芒星 (下図) を使ったパズルはいろいろな種類がありますが、今回は数字を配置するパズルを取り上げます。

五芒星には頂点と交点が 10 ヵ所ありますが、ここに 1 から 10 までの数字を配置します。すると、直線上に 4 つの数字が並びますが、その和が n 本の直線で等しくなるような配置を求める、というものです。このように、数字を星形に配置する魔方陣を「魔星陣」といいます。
3 本の直線で等しくなる配置は、ある本で見かけたことがあります。それでは、4 本の直線が等しくなる配置は何通りあるのでしょうか。プログラムを作って調べてみましょう。
●データ構造の定義
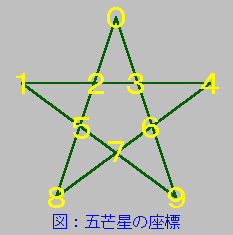
五芒星の 10 ヵ所の点は配列 stars で表します。そして、五芒星の点は下図のように stars の添字と対応づけると、5 本の直線は次に示すデータで表すことができます。
リスト : 直線の定義
SIZE = 10
lines5 = [
[0, 2, 5, 8],
[0, 3, 6, 9],
[1, 2, 3, 4],
[1, 5, 7, 9],
[4, 6, 7, 8]
]
1 行で 1 本の直線を表していることは、図を見ればすぐにわかるでしょう。あとは「生成検定法」の出番です。1 から 10 までの順列を生成して、それが条件を満たしているかチェックすればいいわけです。
●プログラムの作成
最初に、順列を生成して五芒星をチェックするプログラムを作ります。
リスト : 深さ優先探索
def dfs(stars, used):
n = len(stars)
if n == SIZE:
check_stars(stars)
else:
for i in range(1, SIZE + 1):
if used[i] or check_symmetry(stars, n, i): continue
used[i] = True
stars.append(i)
dfs(stars, used)
stars.pop()
used[i] = False
重複解をチェックする関数 check_symmetry() を除くと、今までのプログラムとほぼ同じなので、とくに難しいところはないと思います。check_symmetry() はあとで詳しく説明します。
次に、条件をチェックする関数 check_stars() を作ります。
リスト : 条件のチェック
def write_answer(stars, n):
if n not in result5:
result5[n] = [stars[:]]
else:
result5[n].append(stars[:])
def check_stars(stars):
def add(a, b, c, d):
return stars[a] + stars[b] + stars[c] + stars[d]
total = [add(*ls) for ls in lines5]
if total.count(total[0]) >=4:
write_answer(stars, total[0])
elif total.count(total[1]) >=4:
write_answer(stars, total[1])
各直線の合計値を配列 total に格納します。次に、4 本以上同じ値の直線があるかチェックします。5 本のうち 4 本が同じ値になっているか調べるわけですから、直線 0 と同じ値の本数と、直線 1 と同じ値の本数を調べるだけです。同じ値を 4 つ以上見つけたら、write_answer() で解を result5 (Python の辞書) に記録します。
次は dfs() を呼び出して解を求める関数 five_stars() を作ります。
リスト : 五芒星の問題を解く
def five_stars():
global result5
result5 = {}
dfs([], [False] * (SIZE + 1))
total = 0
for n in result5.keys():
xs = result5[n]
print(n, len(xs), xs[0])
total += len(xs)
print(total)
大域変数 result5 を空の辞書で初期化します。dfs() を呼び出したあと、result5 に記録された解を出力します。なお、今回は直線の和、解の総数、最初に見つけた解を出力しています。
●対称解のチェック
パズルの解法では「対称解」のチェックが必要になる場合があります。対称解とは、盤面を回転させたり裏返しにすると同じになる解のことで、「重複解」と呼ぶこともあります。盤面に対称性がある場合は必ず発生します。五芒星の場合、72 度ずつ回転させると同じ形になりますね。つまり、回転すると同じになる解 (回転解) が 5 つあるわけです。また、五芒星を裏返しにすると、次の図のような配置になります。

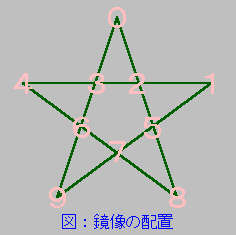
このような解を「鏡像解」といいます。当然ですが、この鏡像解にも回転解が存在します。したがって、重複解のチェックを行わないと、同じ解を 10 通り出力することになります。
五芒星の場合、重複解のチェックは難しい処理ではありません。まず、回転解のチェックですが、0 番で選んだ数字に注目してください。選択した数字が 1 だとすると、五芒星を 72 度ずつ回転していくと、1 は 1 番、8 番、9 番、4 番へと移動していきます。これらは同じ解なのですから、0 番でほかの数字を選んだ場合でも、これらの位置では数字 1 を選ぶ必要はありませんね。ようするに、0 番に配置したことがある数字は、1, 4, 8, 9 番に配置しないことで回転解を取り除くことができるわけです。
次は鏡像解のチェックです。上図の 2 番と 3 番に注目してください。左右の図で 2 つの位置が入れ替わっていますね。ある解の 2 番と 3 番の数字が 2, 10 だったとすると、鏡像解では逆の 10, 2 になるわけです。この数字の大小関係を限定することで、鏡像解をチェックすることができます。
対称解をチェックする関数 check_symmetry() は次のようになります。
リスト : 対称解のチェック
# 0 以外の頂点
vertex = [
False, True, False, False, True,
False, False, False, True, True
]
# 対称解のチェック
def check_symmetry(stars, pos, num):
return (vertex[pos] and stars[0] > num) or (pos == 3 and stars[2] > num)
引数 pos は位置で、num はそこに入れる数字です。配列 vertex は位置 1, 4, 8, 9 を判定するために使います。vertex[pos] が 1 で num が star[0] より小さい場合、num は 0 番に配置したことがある数字です。0 番は 1 から順番に数字がセットされるので、数字の大きさを比較するだけでチェックすることができます。鏡像解のチェックは簡単ですね。
●実行結果
それでは、実行結果を示します。
>>> s = time.time(); five_stars(); print(time.time() - s) 21 60 [1, 2, 4, 8, 7, 10, 3, 5, 6, 9] 23 60 [1, 2, 4, 9, 3, 10, 7, 5, 8, 6] 24 24 [1, 3, 2, 10, 9, 7, 5, 6, 4, 8] 20 24 [1, 3, 6, 7, 4, 8, 2, 9, 5, 10] 168 2.363358974456787 実行環境 : Python3 (ver 3.8.10), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
| 直線の値 | 個数 |
|---|---|
| 20 (30) | 24 |
| 21 (26) | 60 |
| 23 (18) | 60 |
| 24 (14) | 24 |
| 総数 | 168 |
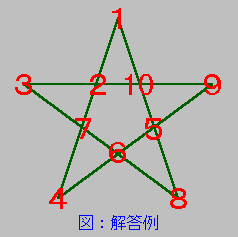
解の総数は 168 通り [*1] になりました。カッコの中は残り 1 本の値を表しています。解答例は、直線の値が 24 の場合です。ところで、直線の値が 20, 21, 23, 24 の 4 通りもあるとは驚きました。
M.Hiroi は、六芒星で 6 本全部の直線が 26 になる場合を調べたことがあります。この場合、解は 80 通りありますが、26 以外の解は存在しません。一般の n 芒星で n 本の和が等しくなる場合について、次の関係が成り立つことを deepgreen さんがゲストブック (No.61) で指摘されました。
直線上の 4 点の和を m とし、n 本の直線の総和を考える。n 本の直線によって、すべての点は丁度 2 回数えられます。従って、
m*n = 2*{1+2+...+2n} = 2*{2n*(2n+1)/2}即ち
m = 2(2n+1)という関係が成り立つことが必要です。
いやー、まいりました。このような関係が成立するとは、M.Hiroi はちっとも気がつきませんでした。この関係から、直線の和がすべて等しくなる場合、その値は 1 通りしかないこともわかりますね。deepgreen さん、ありがとうございました。
[*1] M.Kamada さんに 168 通りで正しいこと、六芒星では 26 以外の解が存在しないことを確認していただきました。M.Kamada さんに感謝いたします。
●5 本の直線の和が等しくなる場合
ところで、書店で立ち読みした本に変形魔方陣の話があり、五芒星の魔方陣も掲載されていました。3 と 7 を除いた 1 から 12 までの数字を配置すると 5 本の直線の和が 24 になるそうです。もしかすると、別の数字の組み合わせがあるかもしれません。さっそくプログラムを作って確かめてみました。
リスト : 五芒星の問題 (1 - 12 の中から 10 個の数字を選ぶ)
def check_stars2(stars):
def add(a, b, c, d):
return stars[a] + stars[b] + stars[c] + stars[d]
total = [add(*ls) for ls in lines5]
if total.count(total[0]) == 5:
print(stars, total[0])
def dfs2(stars, used):
n = len(stars)
if n == SIZE:
check_stars2(stars)
else:
for i in range(1, 13):
if used[i] or check_symmetry(stars, n, i): continue
used[i] = True
stars.append(i)
dfs2(stars, used)
stars.pop()
used[i] = False
def five_stars2():
dfs2([], [False] * 13)
関数 dfs2() で 1 - 12 から 10 個の数字を選ぶ順列を生成し、関数 check_stars2() で 5 本の直線の和が等しいかチェックします。単純な生成検定法なので、難しいところはないでしょう。
●実行結果
実行結果は次のようになりました。
>>> s = time.time(); five_stars2(); print(time.time() - s) [1, 2, 4, 12, 6, 9, 3, 5, 10, 8] 24 [1, 2, 8, 9, 5, 12, 10, 6, 3, 4] 24 [1, 3, 7, 10, 8, 9, 5, 4, 11, 12] 28 [1, 3, 9, 12, 4, 7, 5, 8, 11, 10] 28 [1, 4, 5, 11, 8, 12, 7, 3, 10, 9] 28 [1, 4, 9, 12, 3, 11, 10, 8, 7, 5] 28 [1, 5, 3, 10, 6, 8, 4, 2, 12, 9] 24 [1, 5, 8, 9, 2, 3, 4, 6, 12, 10] 24 [1, 6, 3, 10, 5, 12, 9, 2, 8, 4] 24 [1, 6, 4, 12, 2, 10, 8, 5, 9, 3] 24 [1, 8, 5, 11, 4, 10, 9, 3, 12, 7] 28 [1, 8, 7, 10, 3, 11, 12, 4, 9, 5] 28 [2, 3, 5, 6, 10, 8, 4, 1, 9, 12] 24 [2, 10, 5, 6, 3, 9, 12, 1, 8, 4] 24 [3, 4, 1, 10, 9, 12, 5, 2, 8, 6] 24 [3, 5, 4, 8, 11, 12, 7, 1, 9, 10] 28 [3, 9, 1, 10, 4, 8, 6, 2, 12, 5] 24 [3, 11, 4, 8, 5, 9, 10, 1, 12, 7] 28 [4, 5, 2, 9, 8, 6, 1, 3, 12, 10] 24 [4, 7, 3, 8, 10, 9, 5, 1, 12, 11] 28 [4, 10, 3, 8, 7, 12, 11, 1, 9, 5] 28 [5, 7, 1, 11, 9, 10, 4, 3, 12, 8] 28 [6, 9, 2, 5, 8, 4, 3, 1, 12, 10] 24 [8, 9, 3, 4, 12, 7, 5, 1, 10, 11] 28 72.58757972717285
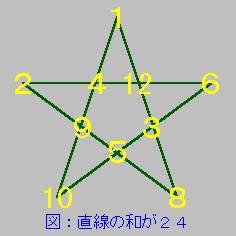
直線の和が 24 になる配置が 12 通り、28 になる配置が 12 通りありました。実行時間は約 73 秒、Python だと時間がかかりますね。PyPy3 で実行したところ約 16 秒になりました。プログラムは対称解のチェックを行っているだけで、ほかの枝刈りはいっさい行っておりません。興味のある方は枝刈りを追加してプログラムの高速化に挑戦してみてください。配置の一例を図に示します。
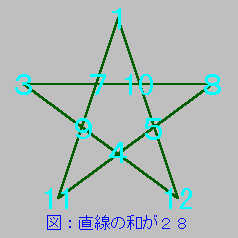
●プログラムリスト
#
# magic.py : 魔方陣
#
# Copyright (C) 2022 Makoto Hiroi
#
import time
# 盤面
# 0 1 2
# 3 4 5
# 6 7 8
# 直線を表す配列
lines = [
[0, 1, 2], [3, 4, 5], [6, 7, 8],
[0, 3, 6], [1, 4, 7], [2, 5, 8],
[0, 4, 8], [2, 4, 6]
]
# チェック
def check(ps):
def add(x, y, z): return ps[x] + ps[y] + ps[z]
xs = [add(*ls) for ls in lines]
return xs.count(xs[0]) == len(xs)
# 解の表示
def print_board(ps):
for i in range(9):
print(ps[i], end=' ')
if (i + 1) % 3 == 0: print()
print()
# 魔方陣の解法 (単純版)
def magic_square(ps = []):
if len(ps) == 9:
if check(ps): print_board(ps)
else:
for n in range(1, 10):
if n not in ps:
ps.append(n)
magic_square(ps)
ps.pop()
# 重複解の排除
def magic_square1(ps = []):
if len(ps) == 9:
if check(ps): print_board(ps)
else:
for n in range(1, 10):
if n not in ps:
if len(ps) == 2 and ps[0] > n: continue
if len(ps) == 6 and ps[2] > n: continue
if len(ps) == 8 and ps[0] > n: continue
ps.append(n)
magic_square1(ps)
ps.pop()
#
# 五芒星の問題
#
SIZE = 10
# 直線の定義
lines5 = [
[0, 2, 5, 8],
[0, 3, 6, 9],
[1, 2, 3, 4],
[1, 5, 7, 9],
[4, 6, 7, 8]
]
# 解を記録する
def write_answer(stars, n):
if n not in result5:
result5[n] = [stars[:]]
else:
result5[n].append(stars[:])
# チェック
def check_stars(stars):
def add(a, b, c, d):
return stars[a] + stars[b] + stars[c] + stars[d]
total = [add(*ls) for ls in lines5]
if total.count(total[0]) >=4:
write_answer(stars, total[0])
elif total.count(total[1]) >=4:
write_answer(stars, total[1])
# 0 以外の頂点
vertex = [
False, True, False, False, True,
False, False, False, True, True
]
# 対称解のチェック
def check_symmetry(stars, pos, num):
return (vertex[pos] and stars[0] > num) or (pos == 3 and stars[2] > num)
# 深さ優先探索
def dfs(stars, used):
n = len(stars)
if n == SIZE:
check_stars(stars)
else:
for i in range(1, SIZE + 1):
if used[i] or check_symmetry(stars, n, i): continue
used[i] = True
stars.append(i)
dfs(stars, used)
stars.pop()
used[i] = False
# 五芒星の問題を解く
def five_stars():
global result5
result5 = {}
dfs([], [False] * (SIZE + 1))
total = 0
for n in result5.keys():
xs = result5[n]
print(n, len(xs), xs[0])
total += len(xs)
print(total)
#
# 1 - 12 の中から 10 個の数字を選ぶ
#
# チェック
def check_stars2(stars):
def add(a, b, c, d):
return stars[a] + stars[b] + stars[c] + stars[d]
total = [add(*ls) for ls in lines5]
if total.count(total[0]) == 5:
print(stars, total[0])
# 深さ優先探索
def dfs2(stars, used):
n = len(stars)
if n == SIZE:
check_stars2(stars)
else:
for i in range(1, 13):
if used[i] or check_symmetry(stars, n, i): continue
used[i] = True
stars.append(i)
dfs2(stars, used)
stars.pop()
used[i] = False
# 問題2を解く
def five_stars2():
dfs2([], [False] * 13)