問題の説明
「ライン・パズル」は、「15 パズル」や「箱入り娘」などで有名なスライディングブロックパズルのひとつです。このパズルは円を四等分した模様のピースを 16 枚使います。それでは問題です。
問題1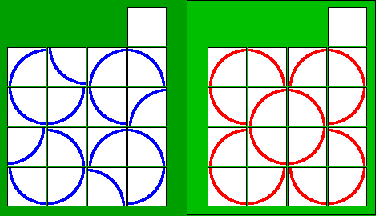
問題2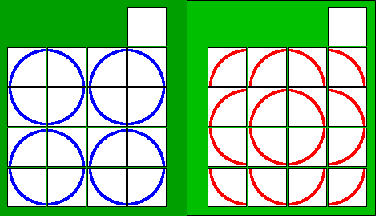
問題3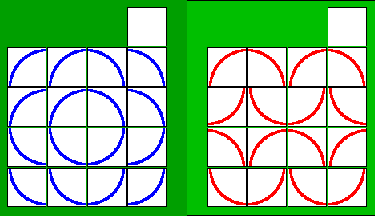
各問題の右図から左図までの最短手数を求めてください。
ライン・パズルの場合、最初に動かすことができるピースは盤面右上のピースしかありません。また、最後は最初に動かしたピースを元に戻して模様が完成することになります。そこで、右上のピースを動かした状態から始めて、そのピースを戻す直前までの手順を求めることにします。したがって、求まる手数は実際の手数よりも 2 手だけ少なくなります。
四等分したピースは、左上を A, 右上を B, 左下を C, 右下を D と名前を付けましょう。A, C, D のピースが 4 つあり、B のピースが 3 つで残りが空き場所ですから、局面の総数は次のようになります。
16C4 * 12C4 * 8C4 * 4 = 1820 * 495 * 70 * 4 = 252,252,000
幅優先探索で解くには大きな数なので、今回は反復深化を使って解くことにします。使用するプログラミング言語は Python3 (PyPy3) です。
●単純な反復深化
まずは、下限値枝刈り法を使わないでプログラムを作ります。いつものように、空いている場所を S (0) で表し、ほかの駒を A (1) から D (4) までの数字で表すことにします。そうすると、問題 1, 2, 3 は次のように表すことができます。
リスト : 大域変数の定義
# 円を四等分
# A B
# C D
# 盤面の大きさ
SIZE = 16
# 駒
S = 0
A = 1
B = 2
C = 3
D = 4
# 問題
start1 = (
A,C,A,S,
C,D,C,A,
D,B,A,B,
C,D,B,D
)
start2 = (
A,B,A,S,
C,D,C,D,
A,B,A,B,
C,D,C,D
)
start3 = (
A,A,B,S,
A,A,B,B,
C,C,D,D,
C,C,D,D
)
goal1 = (
A,B,A,S,
C,A,B,D,
A,C,D,B,
C,D,C,D
)
goal2 = start3
goal3 = (
A,B,A,S,
D,C,D,C,
B,A,B,A,
C,D,C,D
)
反復深化で解を探索する関数 dfs() と solver_ids() は次のようになります。
リスト:反復深化による探索
def dfs(n, board, goal, space, limit, moves):
if n == limit:
if board == goal:
print(moves[1:])
return True
else:
for x in adjacent[space]:
if x == moves[-1][1]: continue
board[space] = board[x]
board[x] = S
moves.append((x, space))
if dfs(n + 1, board, goal, x, limit, moves):
return True
moves.pop()
board[x] = board[space]
board[space] = S
return False
def solver_ids(start, goal):
limit = 2
while True:
print(f'---- {limit} -----')
if dfs(0, start, goal, start.index(S), limit, [(-1, -1)]):
break
limit += 2
関数 dfs() の引数 n が手数、board が盤面、goal はゴールの盤面、space が空き場所の位置、limit が反復深化の上限値、moves が移動手順を表すリストです。このパズルは同じ駒が複数あるので、移動手順は動かす駒の位置で表すことにします。moves の要素はタプル (from, to) で、from が移動する駒の位置、to が移動先の位置です。
n が limit と等しくなったら、goal に到達したかチェックします。そうでなければ、駒を動かして次の盤面を生成します。動かす駒の位置 x が moves[-1][1] と等しい場合、元の盤面に戻るので x にある駒は動かしません。このチェックを入れないと、実行速度はかなり遅くなるので注意してください。
ライン・パズルはスタートとゴールで空き場所の位置が同じになることから、手数は必ず偶数になることがわかります。したがって、反復深化の上限値は 2 手ずつ増やすことができます。solver_ids() では上限値 limit を 2 に初期化して、while ループの中で limit を +2 しています。あとはとくに難しいところはないと思います。詳細はプログラムリストをお読みくださいませ。
●実行結果
さっそく実行してみたのですが、問題 1 でも時間がかかりすぎて、途中であきらめてしまいました。短い手数の問題であれば、単純な反復深化でも解くことができます。たとえば、問題 2 のスタート (start2) から問題 1 のゴール (goal1) までの最短手順は次のようになりました。
>>>> s = time.time(); solver_ids(list(start2), list(goal1)); print(time.time() - s) ---- 2 ----- ---- 4 ----- ---- 6 ----- ---- 8 ----- ---- 10 ----- ---- 12 ----- ---- 14 ----- ---- 16 ----- [(2, 3), (1, 2), (5, 1), (9, 5), (10, 9), (6, 10), (5, 6), (1, 5), (2, 1), (6, 2), (5, 6), (9, 5), (10, 9), (6, 10), (2, 6), (3, 2)] 0.03650331497192383 実行環境 : PyPy3 (ver 7.3.1), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
単純な反復深化の場合、M.Hiroi の環境では 20 手程度の探索が限界かもしれません。そこで、「下限値枝刈り法」を使ってプログラムの高速化に挑戦してみましょう。
●下限値枝刈り法による高速化
さて、下限値を求める方法ですが、これにはいろいろな方法が考えられます。今回は、各駒が正しい位置へ移動するまでの手数を下限値として利用することにします。たとえば、「8 パズル」の場合は次のように求めることができます。
┌─┬─┬─┐ ┌──┬──┬──┐
│1│2│3│ │8(3)│6(2)│7(4)│
├─┼─┼─┤ ├──┼──┼──┤
│4│5│6│ │2(2)│5(0)│4(2)│
├─┼─┼─┤ ├──┼──┼──┤
│7│8│ │ │3(4)│ │1(4)│
└─┴─┴─┘ └──┴──┴──┘
(n) : n は移動手数
(1) 完成形 (2) 初期状態:合計 21 手
図 : 「8 パズル」下限値の求め方
右下にある 1 の駒を左上の正しい位置に移動するには、最低でも 4 手必要です。もちろん、ほかの駒との関連で、それ以上の手数が必要になる場合もあるでしょうが、4 手より少なくなることは絶対にありません。同じように、各駒について最低限必要な手数を求めることができます。そして、その合計値はパズルを解くのに最低限必要な手数となります。これを下限値として利用することができます。
同じ駒が複数ある「ライン・パズル」の場合、この方法をそのまま適用することはできません。そこで、下限値の精度は低くなりますが、目標の位置にいちばん近い駒の移動手数を使うことにします。次の図を見てください。
┌─┬─┬─┬─┐ ┌─┬─┬─┬─┐ │A│C│A│S│ │A1│B│A2│S│ ├─┼─┼─┼─┤ ├─┼─┼─┼─┤ │C│D│C│A│ │C│D│C│D│ ├─┼─┼─┼─┤ ├─┼─┼─┼─┤ │D│B│A│B│ │A4│B│A3│B│ ├─┼─┼─┼─┤ ├─┼─┼─┼─┤ │C│D│B│D│ │C│D│C│D│ └─┴─┴─┴─┘ └─┴─┴─┴─┘ (1) 完成形 (2) 初期状態 図 : 「ライン・パズル」下限値の求め方
駒 A に注目してください。完成形と初期状態を比べると、A1, A2, A3 の駒は正しい位置にあるので、移動手数は 0 でいいですね。A4 の移動手数ですが、残りひとつの位置へ移動するまでの手数ではなく、A4 にいちばん近い位置へ移動する手数を求めます。この場合、A1 か A3 の駒がある位置がいちばん近いので、移動手数は 2 となります。このように、駒が重複する場合もあるため下限値の精度は低下しますが、いちばん近い位置までの移動手数を求めるだけなのでプログラムは簡単になります。
下限値の求め方ですが、駒を動かすたびに各駒の手数を計算していたのでは時間がかかります。「ライン・パズル」の場合、1 回にひとつの駒しか移動しないので、初期状態の下限値を求めておいて、動かした駒の差分だけを計算すればいいでしょう。また、駒の移動手数はいちいち計算するのではなく、あらかじめ計算した結果を配列に格納しておいた方が良いでしょう。プログラムは次のようになります。
リスト : 移動手数表の作成
# 移動手数表を作る
def make_distance(goal):
d = [[0] * SIZE]
for p in range(1, 5):
xs = []
ys = []
for i, x in enumerate(goal):
if x == p:
xs.append((i % 4, i // 4))
for i in range(SIZE):
if goal[i] == p:
m = 0
else:
x1 = i % 4
y1 = i // 4
m = min([abs(x - x1) + abs(y - y1) for x, y in xs])
ys.append(m)
d.append(ys)
return d
# 下限値を求める
def get_lower_value(b):
lower = 0
for i, p in enumerate(b):
lower += distance[p][i]
return lower
移動手数表は関数 make_distance() で生成して、大域変数 distance にセットします。リスト d が生成する移動手数表を表します。最初に、d[0] にダミーデータをセットします。次に、正しい駒の位置を座標 (x, y) に変換してリスト xs に格納します。あとは、内包表記で正しい位置までの移動手数をリストに格納し、その中から min() で最短手数を求めて、リスト ys に追加していきます。すべての場所を調べたら、ys を d に追加します。
次は、下限値枝刈り法のプログラムを作ります。
リスト : 下限値枝刈り法
def dfs1(n, board, goal, space, limit, lower, moves):
if n == limit:
if board == goal:
print(moves[1:])
return True
else:
for x in adjacent[space]:
if x == moves[-1][1]: continue
p = board[x]
newlower = lower - distance[p][x] + distance[p][space]
if n + newlower > limit: continue
board[space] = p
board[x] = S
moves.append((x, space))
if dfs1(n + 1, board, goal, x, limit, newlower, moves):
return True
moves.pop()
board[x] = p
board[space] = S
return False
def solver_ids1(start, goal):
global distance
distance = make_distance(goal)
lower = get_lower_value(start)
if lower % 2 == 1: lower += 1
limit = lower
while True:
print(f'---- {limit} -----')
if dfs1(0, start, goal, start.index(0), limit, lower, [(-1, -1)]):
break
limit += 2
関数 dfs1() の引数 lower が下限値を表します。駒を動かしたら差分を計算して、新しい下限値 newlower を求ます。そして、newlower + n が上限値 limit を越えたら枝刈りを行います。limit 以下であれば dfs1() を再帰呼び出しします。追加する処理はこれだけで、あとは反復深化のプログラムと同じです。
solver_ids1() では、make_distance() で移動手数表を生成して大域変数 distance にセットします。次に、get_lower_value() を呼び出して下限値を求め、変数 lower にセットします。lower が奇数の場合は +1 します。上限値 limit は lower から開始します。
あとは今までの下限値枝刈り法のプログラムと変わらないので、説明は割愛させていただきます。詳細はプログラムリストをお読みくださいませ。
●実行結果
それでは実行結果を示します。
>>>> s = time.time(); solver_ids1(list(start1), list(goal1)); print(time.time() - s) ---- 16 ----- ---- 18 ----- ---- 20 ----- ---- 22 ----- ---- 24 ----- ---- 26 ----- ---- 28 ----- ---- 30 ----- [(7, 3), (6, 7), (5, 6), (9, 5), (10, 9), (14, 10), (15, 14), (11, 15), (7, 11), (6, 7), (5, 6), (9, 5), (8, 9), (4, 8), (0, 4), (1, 0), (2, 1), (6, 2), (10, 6), (11, 10), (15, 11), (14, 15), (10, 14), (9, 10), (8, 9), (4, 8), (0, 4), (1, 0), (2, 1), (3, 2)] 0.22143316268920898 >>>> s = time.time(); solver_ids1(list(start2), list(goal2)); print(time.time() - s) ---- 16 ----- ---- 18 ----- ---- 20 ----- ---- 22 ----- ---- 24 ----- ---- 26 ----- ---- 28 ----- ---- 30 ----- ---- 32 ----- [(2, 3), (1, 2), (5, 1), (6, 5), (10, 6), (9, 10), (5, 9), (6, 5), (7, 6), (11, 7), (10, 11), (6, 10), (2, 6), (3, 2), (7, 3), (11, 7), (10, 11), (14, 10), (13, 14), (9, 13), (8, 9), (4, 8), (5, 4), (1, 5), (2, 1), (6, 2), (5, 6), (9, 5), (10, 9), (6, 10), (2, 6), (3, 2)] 0.6979901790618896 >>>> s = time.time(); solver_ids1(list(start3), list(goal3)); print(time.time() - s) ---- 14 ----- ---- 16 ----- ---- 18 ----- ---- 20 ----- ---- 22 ----- ---- 24 ----- ---- 26 ----- ---- 28 ----- ---- 30 ----- ---- 32 ----- ---- 34 ----- ---- 36 ----- ---- 38 ----- [(2, 3), (1, 2), (5, 1), (6, 5), (7, 6), (3, 7), (2, 3), (1, 2), (5, 1), (6, 5), (10, 6), (9, 10), (8, 9), (4, 8), (5, 4), (6, 5), (10, 6), (9, 10), (13, 9), (14, 13), (10, 14), (9, 10), (8, 9), (4, 8), (5, 4), (6, 5), (10, 6), (11, 10), (7, 11), (6, 7), (2, 6), (3, 2), (7, 3), (6, 7), (10, 6), (11, 10), (7, 11), (3, 7)] 138.16579127311707 実行環境 : PyPy3 (ver 7.3.1), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
問題 1 は 30 + 2 = 32 手、問題 2 は 32 + 2 = 34 手、問題 3 は 38 + 2 = 40 手で解くことができました。このほかに、問題の盤面を組み合わせて試してみたところ、結果は次のようになりました。
表 : ライン・パズルの実行結果 (単位 : 秒)
: 下限値 : 手数 : 時間
-------------------+--------+--------+-------
start1 <==> start2 : 8 : 30(32) : 0.81
start3 : 20 : 30(32) : 0.20
goal1 : 16 : 30(32) : 0.22
goal3 : 10 : 24(26) : 0.036
-------------------+--------+--------+-------
start2 <==> start3 : 16 : 32(34) : 0.70
goal1 : 8 : 16(18) : 0.003
goal3 : 8 : 24(26) : 0.032
-------------------+--------+--------+-------
start3 <==> goal1 : 8 : 22(24) : 0.016
goal3 : 14 : 38(40) : 138.2
-------------------+--------+--------+-------
goal1 <==> goal3 : 8 : 28(30) : 0.41
下限値の精度が低いので、問題 3 (start3, goal3) のような長手数になると PyPy3 でも時間がかかります。下限値の精度を改善できればいいのですが、M.Hiroi にはちょっと思いつきません (苦笑)。興味のある方は、プログラムを改良してみてください。
●プログラムリスト
#
# linepuz.py : ライン・パズル
#
# Copyright (C) 2022 Makoto Hiroi
#
import time
# 盤面の大きさ
SIZE = 16
# 駒
S = 0
A = 1
B = 2
C = 3
D = 4
# 隣接リスト
adjacent = [
[1, 4], # 0
[0, 2, 5], # 1
[1, 3, 6], # 2
[2, 7], # 3
[0, 5, 8], # 4
[1, 4, 6, 9], # 5
[2, 5, 7, 10], # 6
[3, 6, 11], # 7
[4, 9, 12], # 8
[5, 8, 10, 13], # 9
[6, 9, 11, 14], # 10
[7, 10, 15], # 11
[8, 13], # 12
[9, 12, 14], # 13
[10, 13, 15], # 14
[11, 14] # 15
]
# 問題
start1 = (
A,C,A,S,
C,D,C,A,
D,B,A,B,
C,D,B,D
)
start2 = (
A,B,A,S,
C,D,C,D,
A,B,A,B,
C,D,C,D
)
start3 = (
A,A,B,S,
A,A,B,B,
C,C,D,D,
C,C,D,D
)
goal1 = (
A,B,A,S,
C,A,B,D,
A,C,D,B,
C,D,C,D
)
goal2 = start3
goal3 = (
A,B,A,S,
D,C,D,C,
B,A,B,A,
C,D,C,D
)
# 反復深化
def dfs(n, board, goal, space, limit, moves):
if n == limit:
if board == goal:
print(moves[1:])
return True
else:
for x in adjacent[space]:
if x == moves[-1][1]: continue
board[space] = board[x]
board[x] = S
moves.append((x, space))
if dfs(n + 1, board, goal, x, limit, moves):
return True
moves.pop()
board[x] = board[space]
board[space] = S
return False
def solver_ids(start, goal):
limit = 2
while True:
print(f'---- {limit} -----')
if dfs(0, start, goal, start.index(S), limit, [(-1, -1)]):
break
limit += 2
# 移動手数表を作る
def make_distance(goal):
d = [[0] * SIZE]
for p in range(1, 5):
xs = []
ys = []
for i, x in enumerate(goal):
if x == p:
xs.append((i % 4, i // 4))
for i in range(SIZE):
if goal[i] == p:
m = 0
else:
x1 = i % 4
y1 = i // 4
m = min([abs(x - x1) + abs(y - y1) for x, y in xs])
ys.append(m)
d.append(ys)
return d
# 下限値を求める
def get_lower_value(b):
lower = 0
for i, p in enumerate(b):
lower += distance[p][i]
return lower
# 反復深化+下限値枝刈り法
def dfs1(n, board, goal, space, limit, lower, moves):
if n == limit:
if board == goal:
print(moves[1:])
return True
else:
for x in adjacent[space]:
if x == moves[-1][1]: continue
p = board[x]
newlower = lower - distance[p][x] + distance[p][space]
if n + newlower > limit: continue
board[space] = p
board[x] = S
moves.append((x, space))
if dfs1(n + 1, board, goal, x, limit, newlower, moves):
return True
moves.pop()
board[x] = p
board[space] = S
return False
def solver_ids1(start, goal):
global distance
distance = make_distance(goal)
lower = get_lower_value(start)
if lower % 2 == 1: lower += 1
limit = lower
while True:
print(f'---- {limit} -----')
if dfs1(0, start, goal, start.index(0), limit, lower, [(-1, -1)]):
break
limit += 2