問題の説明
今回はもう少しだけサイズを大きくしたペグ・ソリテアに挑戦してみましょう。
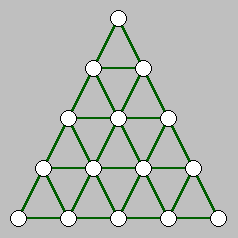
上図は「チャイニーズ・チェッカー」と呼ばれるペグ・ソリテアです。15 個の点が三角形に並んでいて、そこにペグを配置します。ペグは別のペグをひとつだけ跳び超えることで、任意の方向へ移動することができます。もちろん、着地する地点が空いていなければ、跳び越えることはできません。15 個のペグの中からひとつのペグを取り除き、最後にひとつだけペグが残る跳び方の最短手数を求めることにします。
●プログラムを作る
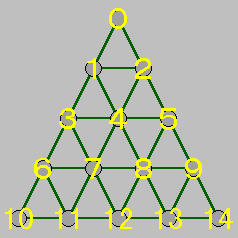
それではプログラムを作りましょう。使用するプログラミング言語は Python3 (ver 3.8.01) です。まず、ペグの跳び先表を定義します。下図のように座標を定義すると、跳び先表は次のようになります。
リスト : 定数と跳び先表の定義
# 定数
MAX_JUMP = 13
SIZE = 15
# 跳び先表
jump_table = [
[(1, 3), (2, 5)], # 0
[(3, 6), (4, 8)], # 1
[(4, 7), (5, 9)], # 2
[(1, 0), (4, 5), (6, 10), (7, 12)], # 3
[(7, 11), (8, 13)], # 4
[(2, 0), (4, 3), (8, 12), (9, 14)], # 5
[(3, 1), (7, 8)], # 6
[(4, 2), (8, 9)], # 7
[(4, 1), (7, 6)], # 8
[(5, 2), (8, 7)], # 9
[(6, 3), (11, 12)], # 10
[(7, 4), (12, 13)], # 11
[(7, 3), (8, 5), (11, 10), (13, 14)], # 12
[(8, 4), (12, 11)], # 13
[(9, 5), (13, 12)],
]
ペグが 13 回移動すると盤上のペグはひとつになるので、MAX_JUMP は 13 となります。
次は解を求める関数 solver() を修正します。
リスト : チャイニーズ・チェッカーの解法
def solver(from_, del_, to_):
global cnt
cnt = 0
board = [True] * SIZE
# 初手を from_ -> to_ に限定
board[from_] = False
board[del_] = False
for i in range(1, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 0, i, [(from_, to_)])
if cnt > 0: break
print(cnt)
引数 from_, del_, to_ で初手を指定するように変更しただけです。あとのプログラムは Hoppers とほとんど同じなので説明は割愛します。詳細はプログラムリストをお読みください。
●実行結果
それでは最短手数を求めてみましょう。盤面の対称性から穴の位置は 0, 1, 3, 4 の 4 つを調べれば OK です。初手の選び方も対称性を考えると次の 6 通りに限定することができます。
(1) 3 -> 1 -> 0 (2) 6 -> 3 -> 1 (3) 8 -> 4 -> 1 (4) 0 -> 1 -> 3 (5) 5 -> 4 -> 3 (6) 11 -> 7 -> 4
それでは実行結果を示します。
: 手数 : 総数
----+------+------
(1) : 9 : 950
(2) : 9 : 950
(3) : -- : 0
(4) : 8 : 280
(5) : 9 : 1151
(6) : 10 : 154
辺の中央のペグを取り除き、最初に頂点のペグを移動する (4) が最短手数 (8 手) になりました。移動手順は 280 通り、その一部を以下に示します。
>>> solver(0,1,3) ----- 1 ----- ----- 2 ----- ----- 3 ----- ----- 4 ----- ----- 5 ----- ----- 6 ----- ----- 7 ----- ----- 8 ----- [0, 3][6, 1][5, 0, 3, 5][9, 2][11, 4][13, 11][10, 12, 5][2, 9][14, 5, 3] [0, 3][6, 1][5, 0, 3, 5][9, 2][12, 5][2, 9][10, 12][13, 11, 4][14, 5, 3] [0, 3][6, 1][5, 0, 3, 5][9, 2][12, 5][10, 12][2, 9][13, 11, 4][14, 5, 3] ・・・省略・・・ [0, 3][6, 1][12, 3][14, 12][11, 13][9, 7][1, 6][2, 9][10, 3, 12, 14, 5, 3] [0, 3][6, 1][12, 3][14, 12][11, 13][9, 7][2, 9][1, 6][10, 3, 5, 14, 12, 3] [0, 3][6, 1][12, 3][14, 12][11, 13][9, 7][2, 9][1, 6][10, 3, 12, 14, 5, 3] 280
最後のペグの位置は 3 と 14 の 2 通りがあり、補償型の解があることがわかります。
●プログラムリスト
#
# peg15.py : チャイニーズ・チェッカー (ペグ・ソリティア)
#
# Copyright (C) 2022 Makoto Hiroi
#
# 定数
MAX_JUMP = 13
SIZE = 15
# 跳び先表
jump_table = [
[(1, 3), (2, 5)], # 0
[(3, 6), (4, 8)], # 1
[(4, 7), (5, 9)], # 2
[(1, 0), (4, 5), (6, 10), (7, 12)], # 3
[(7, 11), (8, 13)], # 4
[(2, 0), (4, 3), (8, 12), (9, 14)], # 5
[(3, 1), (7, 8)], # 6
[(4, 2), (8, 9)], # 7
[(4, 1), (7, 6)], # 8
[(5, 2), (8, 7)], # 9
[(6, 3), (11, 12)], # 10
[(7, 4), (12, 13)], # 11
[(7, 3), (8, 5), (11, 10), (13, 14)], # 12
[(8, 4), (12, 11)], # 13
[(9, 5), (13, 12)],
]
# 手順の表示
def print_move(xs):
from_, to_ = xs[0]
print(f'[{from_}, {to_}', end='')
prev = to_
for from_, to_ in xs[1:]:
if prev == from_:
print(f', {to_}', end='')
else:
print(f'][{from_}, {to_}', end='')
prev = to_
print(']')
# 反復深化
def dfs(board, jc, limit, move):
global cnt
if jc > limit: return
if len(move) == MAX_JUMP:
print_move(move)
cnt += 1
else:
for from_ in range(SIZE):
if not board[from_]: continue
for del_, to_ in jump_table[from_]:
if not board[del_] or board[to_]: continue
board[from_] = False
board[del_] = False
board[to_] = True
if move[-1][1] == from_:
newjc = jc
else:
newjc = jc + 1
move.append((from_, to_))
dfs(board, newjc, limit, move)
move.pop()
board[from_] = True
board[del_] = True
board[to_] = False
def solver(from_, del_, to_):
global cnt
cnt = 0
board = [True] * SIZE
# 初手を from_ -> to_ に限定
board[from_] = False
board[del_] = False
for i in range(1, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 0, i, [(from_, to_)])
if cnt > 0: break
print(cnt)