問題の説明
またまた少しだけサイズを大きくした「ペグ・ソリテア」に挑戦しましょう。
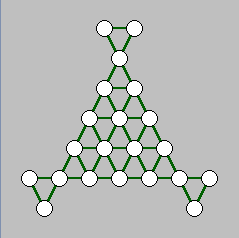
上図は「変形三角盤」と呼ばれるペグ・ソリテアです。21 個のマスが少し変わった三角形に並んでいて、そこにペグを配置します。ペグは別のペグをひとつだけ跳び超えることで、任意の方向へ移動することができます。もちろん、着地する地点が空いていなければ、跳び越えることはできません。今回は中央のペグを取り除き、最後にペグが中央にひとつ残る跳び方 (中央補償型の解) の最短手数を求めることにします。
●プログラムを作る
それではプログラムを作りましょう。使用するプログラミング言語は Python3 ですが、盤面が大きくなると Python3 では荷が重いので、今回は PyPy3 (ver 7.3.1) を使うことにします。最初に、ペグの跳び先表を定義します。下図のように座標を定義すると、跳び先表は次のようになります。
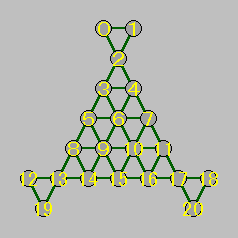
リスト : 跳び先表の定義
# 定数
MAX_JUMP = 19
HOLE = 6
SIZE = 21
# 跳び先表
jump_table = [
[(2, 4)], # 0
[(2, 3)], # 1
[(3, 5), (4, 7)], # 2
[(2, 1), (5, 8), (6, 10)], # 3
[(2, 0), (6, 9), (7, 11)], # 4
[(3, 2), (6, 7), (8, 13), (9, 15)], # 5
[(9, 14), (10, 16)], # 6
[(4, 2), (6, 5), (10, 15), (11, 17)], # 7
[(5, 3), (9, 10), (13, 19)], # 8
[(6, 4), (10, 11)], # 9
[(6, 3), (9, 8)], # 10
[(7, 4), (10, 9), (17, 20)], # 11
[(13, 14)], # 12
[(8, 5), (14, 15)], # 13
[(9, 6), (13, 12), (15, 16)], # 14
[(9, 5), (10, 7), (14, 13), (16, 17)],# 15
[(10, 6), (15, 14), (17, 18)], # 16
[(11, 7), (16, 15)], # 17
[(17, 16)], # 18
[(13, 8)], # 19
[(17, 11)], # 20
]
変形三角盤を解く関数 solver() は次のようになります。
リスト : 変形三角盤の解法
def solver():
global cnt
cnt = 0
board = [True] * SIZE
# 初手を 14 -> 6 に限定
board[14] = False
board[9] = False
for i in range(2, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 1, i, [(14, 6)])
if cnt > 0: break
print(cnt)
今回は初手を 14 -> 6 に限定します。あとのプログラムは Hoppers と同じなので説明は割愛します。詳細はプログラムリストをお読みください。
●実行結果
それでは実行してみましょう。
>>>> s = time.time(); solver(); print(time.time() - s) ----- 2 ----- ----- 3 ----- ----- 4 ----- ----- 5 ----- ----- 6 ----- ----- 7 ----- ----- 8 ----- ----- 9 ----- ----- 10 ----- ----- 11 ----- ----- 12 ----- [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 2, 7, 5, 13][20, 11, 9] [15, 17][19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 2, 7, 5, 13][20, 11, 9] [19, 8, 10][15, 17][18, 16, 6] [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 7, 2, 5, 13][20, 11, 9] [15, 17][19, 8, 10][18, 16, 6] ・・・省略・・・ [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][1, 3][15, 17][7, 2][0, 4][5, 7, 2, 5, 13] [19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][15, 17][1, 3][7, 2][0, 4][5, 2, 7, 5, 13] [19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][15, 17][1, 3][7, 2][0, 4][5, 7, 2, 5, 13] [19, 8, 10][18, 16, 6] 96 579.0008935928345 実行環境 : PyPy3 (ver 7.3.1), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
最短手数は 12 手、解は全部で 96 通りあります。実行時間は約 9 分 40 秒かかりました。解を一つ求めるだけでよければ、もっと速くなります。dfs() の最初の if 文を次のように修正します。
リスト : 解を一つ求める場合
def dfs(board, jc, limit, move):
global cnt
if jc > limit or cnt > 0: return
・・・省略・・・
実行時間は約 5 分 30 秒になりました。それでも、単純な反復深化では時間がかかりますね。そこで、次回は反復深化の常套手段である「下限値枝刈り法」を使ってプログラムの高速化に挑戦しましょう。
●プログラムリスト
#
# peg21.py : 変形三角盤 (ペグ・ソリティア)
#
# Copyright (C) 2022 Makoto Hiroi
#
# 定数
MAX_JUMP = 19
HOLE = 6
SIZE = 21
# 跳び先表
jump_table = [
[(2, 4)], # 0
[(2, 3)], # 1
[(3, 5), (4, 7)], # 2
[(2, 1), (5, 8), (6, 10)], # 3
[(2, 0), (6, 9), (7, 11)], # 4
[(3, 2), (6, 7), (8, 13), (9, 15)], # 5
[(9, 14), (10, 16)], # 6
[(4, 2), (6, 5), (10, 15), (11, 17)], # 7
[(5, 3), (9, 10), (13, 19)], # 8
[(6, 4), (10, 11)], # 9
[(6, 3), (9, 8)], # 10
[(7, 4), (10, 9), (17, 20)], # 11
[(13, 14)], # 12
[(8, 5), (14, 15)], # 13
[(9, 6), (13, 12), (15, 16)], # 14
[(9, 5), (10, 7), (14, 13), (16, 17)],# 15
[(10, 6), (15, 14), (17, 18)], # 16
[(11, 7), (16, 15)], # 17
[(17, 16)], # 18
[(13, 8)], # 19
[(17, 11)], # 20
]
# 手順の表示
def print_move(xs):
from_, to_ = xs[0]
print(f'[{from_}, {to_}', end='')
prev = to_
for from_, to_ in xs[1:]:
if prev == from_:
print(f', {to_}', end='')
else:
print(f'][{from_}, {to_}', end='')
prev = to_
print(']')
# 反復深化
def dfs(board, jc, limit, move):
global cnt
if jc > limit: return
if len(move) == MAX_JUMP:
if board[HOLE]:
print_move(move)
cnt += 1
else:
for from_ in range(SIZE):
if not board[from_]: continue
for del_, to_ in jump_table[from_]:
if not board[del_] or board[to_]: continue
board[from_] = False
board[del_] = False
board[to_] = True
if move[-1][1] == from_:
newjc = jc
else:
newjc = jc + 1
move.append((from_, to_))
dfs(board, newjc, limit, move)
move.pop()
board[from_] = True
board[del_] = True
board[to_] = False
def solver():
global cnt
cnt = 0
board = [True] * SIZE
# 初手を 14 -> 6 に限定
board[14] = False
board[9] = False
for i in range(2, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 1, i, [(14, 6)])
if cnt > 0: break
print(cnt)