プログラムの高速化
変形三角盤の続きです。今回は変形三角盤を解くプログラムの高速化に挑戦してみましょう。最初に反復深化の常套手段である「下限値枝刈り法」を説明します。
●下限値枝刈り法
下限値枝刈り法は難しいアルゴリズムではありません。たとえば、5 手進めた局面を考えてみます。探索の上限が 10 手とすると、あと 5 手だけ動かすことができますね。このとき、パズルを解くのに 6 手以上かかることがわかれば、ここで探索を打ち切ることができます。このように、必要となる最低限の手数が明確にわかる場合、この値を「下限値 (Lower Bound)」と呼びます。下限値を求めることができれば、「今の移動手数 + 下限値」が探索手数を超えた時点で、枝刈りすることが可能になります。これが下限値枝刈り法の基本的な考え方です。
ペグ・ソリテアの場合、コーナーにあるペグはほかのペグから跳び越されることはありません。つまり、コーナーのペグは自分でジャンプするしか移動する方法がないのです。したがって、コーナーにペグが残っていれば、最低でもその個数だけ移動手数が必要になります。変形三角盤の場合、コーナーは 0, 1, 12, 18, 19, 20 番の 6 か所あります。今回はこれを下限値として利用することにしましょう。
コーナーペグを判定するため配列 corner を定義します。
リスト : コーナーペグの位置
corner = [
True, True, False, False, False,
False, False, False, False, False,
False, False, True, False, False,
False, False, False, True, True,
True
]
0, 1, 12, 18, 19, 20 を True に、あとは False に設定します。
●下限値枝刈り法のプログラム
下限値枝刈り法のプログラムは次のようになります。
リスト : 下限値枝刈り法による探索
def dfs(board, jc, limit, lower, move):
global cnt
if jc + lower > limit: return
if len(move) == MAX_JUMP:
if board[HOLE]:
print_move(move)
cnt += 1
else:
for from_ in range(SIZE):
if not board[from_]: continue
for del_, to_ in jump_table[from_]:
if not board[del_] or board[to_]: continue
board[from_] = False
board[del_] = False
board[to_] = True
newjc = jc
if move[-1][1] != from_: newjc += 1
newlower = lower
if corner[from_]: newlower -= 1
if corner[to_]: newlower += 1
move.append((from_, to_))
dfs(board, newjc, limit, newlower, move)
move.pop()
board[from_] = True
board[del_] = True
board[to_] = False
引数 lower が下限値を表します。jc + lower が limit より大きくなったら return で探索を打ち切ります。ペグを動かすとき、from_ と to_ がコーナーペグかチェックします。変数 newlower を lower に初期化しておいて、from_ がコーナーペグならば newlower を -1 します。to_ がコーナーペグならば newlower を +1 します。これだけの修正で下限値枝刈り法が機能します。とても簡単ですね。
最後に dfs() を呼び出す関数 solver() を修正します。
リスト : 下限値枝刈り法
def solver():
global cnt
cnt = 0
board = [True] * SIZE
# 初手を 14 -> 6 に限定
board[14] = False
board[9] = False
for i in range(7, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 1, i, 6, [(14, 6)])
if cnt > 0: break
print(cnt)
下限値の初期値は 6 で初手に移動するペグはコーナーにはありません。上限値 i は 6 + 1 = 7 から始めます。あとは特に難しいところはないので説明は割愛いたします。詳細はプログラムリストをお読みください。
●実行結果
それでは実行してみましょう。
>>>> s = time.time(); solver(); print(time.time() - s) ----- 7 ----- ----- 8 ----- ----- 9 ----- ----- 10 ----- ----- 11 ----- ----- 12 ----- [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 2, 7, 5, 13][20, 11, 9] [15, 17][19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 2, 7, 5, 13][20, 11, 9] [19, 8, 10][15, 17][18, 16, 6] [14, 6][11, 9][3, 10][1, 3][7, 2][0, 4][12, 14, 6][5, 7, 2, 5, 13][20, 11, 9] [15, 17][19, 8, 10][18, 16, 6] ・・・省略・・・ [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][1, 3][15, 17][7, 2][0, 4][5, 7, 2, 5, 13] [19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][15, 17][1, 3][7, 2][0, 4][5, 2, 7, 5, 13] [19, 8, 10][18, 16, 6] [14, 6][11, 9][3, 10][12, 14, 6][20, 11, 9][15, 17][1, 3][7, 2][0, 4][5, 7, 2, 5, 13] [19, 8, 10][18, 16, 6] 96 6.033816576004028 実行環境 : PyPy3 (ver 7.3.1), Ubunts 20.04 (WSL1), Intel Core i5-6200U 2.30GHz
実行時間は約 6 秒でした。約 97 倍の高速化に成功しました。下限値枝刈り法の効果はとても高いですね。
●ペグのグループ分け
このほかに、ペグをグループに分けることで枝刈りを行うことができます。ペグは移動できる場所が決まっていて、下図 (右) のようなグループに分けることができます。
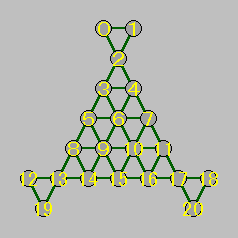
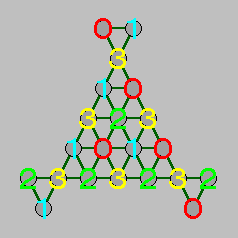
盤面の座標と見比べてください。たとえば、座標 0 番のペグは 4, 9, 11, 20 番にしか移動することができません。逆にいえば、この場所にあるペグは、これ以外の場所へ移動することはできないのです。これらのペグをひとつのグループとして考えましょう。同じようにペグの移動場所によって、上図のように 4 つのグループに分けることができます。
ペグは移動しても所属するグループは変わりませんし、跳び越すペグは必ずほかのグループのペグになります。ここで、グループ 3 とコーナーペグの個数に注目してください。コーナーペグの移動にはグループ 3 のペグが必要になりますが、コーナーペグの数は 6 つ、グループ 3 のペグの数も 6 つですから同じ個数しかありません。
したがって、コーナー以外のペグがグループ 3 のペグを跳び越すと、コーナーペグの移動ができなくなります。つまり、3, 4, 8, 11, 14, 16 番のペグは、グループ 3 のペグを跳び越すことはできないのです。グループ 3 のペグを跳び越すことができるのはコーナーペグだけです。
この枝刈りは跳び先表を変更することで実現できます。修正は次のようになります。
リスト : 跳び先表
jump_table_1 = [
[(2, 4)], # 0
[(2, 3)], # 1
[(3, 5), (4, 7)], # 2
[(6, 10)], # [(2, 1), (5, 8), (6, 10)], # 3
[(6, 9)], # [(2, 0), (6, 9), (7, 11)], # 4
[(3, 2), (6, 7), (8, 13), (9, 15)], # 5
[(9, 14), (10, 16)], # 6
[(4, 2), (6, 5), (10, 15), (11, 17)], # 7
[(9, 10)], # [(5, 3), (9, 10), (13, 19)], # 8
[(6, 4), (10, 11)], # 9
[(6, 3), (9, 8)], # 10
[(10, 9)], # [(7, 4), (10, 9), (17, 20)], # 11
[(13, 14)], # 12
[(8, 5), (14, 15)], # 13
[(9, 6)], # [(9, 6), (13, 12), (15, 16)], # 14
[(9, 5), (10, 7), (14, 13), (16, 17)],# 15
[(10, 6)], # [(10, 6), (15, 14), (17, 18)], # 16
[(11, 7), (16, 15)], # 17
[(17, 16)], # 18
[(13, 8)], # 19
[(17, 11)], # 20
]
さっそく実行してみたところ、実行時間は約 6 秒から約 2 秒に短縮しました。解を一つ求めるだけでよければ、実行時間は 0.93 秒になります。1 秒を切ったので、高速化はここまでにしておきましょう。
下限値枝刈り法の場合、下限値の精度によって実行時間が大きく左右されます。今回は単純な方法で下限値を求めましたが、もっとクールな方法があるかもしれません。興味のある方はいろいろ試してみてください。
●プログラムリスト
#
# peg21a.py : 変形三角盤 (ペグ・ソリティア)
#
# 下限値枝刈り法による高速化
#
# Copyright (C) 2022 Makoto Hiroi
#
# 定数
MAX_JUMP = 19
HOLE = 6
SIZE = 21
# 跳び先表
jump_table = [
[(2, 4)], # 0
[(2, 3)], # 1
[(3, 5), (4, 7)], # 2
[(2, 1), (5, 8), (6, 10)], # 3
[(2, 0), (6, 9), (7, 11)], # 4
[(3, 2), (6, 7), (8, 13), (9, 15)], # 5
[(9, 14), (10, 16)], # 6
[(4, 2), (6, 5), (10, 15), (11, 17)], # 7
[(5, 3), (9, 10), (13, 19)], # 8
[(6, 4), (10, 11)], # 9
[(6, 3), (9, 8)], # 10
[(7, 4), (10, 9), (17, 20)], # 11
[(13, 14)], # 12
[(8, 5), (14, 15)], # 13
[(9, 6), (13, 12), (15, 16)], # 14
[(9, 5), (10, 7), (14, 13), (16, 17)],# 15
[(10, 6), (15, 14), (17, 18)], # 16
[(11, 7), (16, 15)], # 17
[(17, 16)], # 18
[(13, 8)], # 19
[(17, 11)], # 20
]
jump_table_1 = [
[(2, 4)], # 0
[(2, 3)], # 1
[(3, 5), (4, 7)], # 2
[(6, 10)], # [(2, 1), (5, 8), (6, 10)], # 3
[(6, 9)], # [(2, 0), (6, 9), (7, 11)], # 4
[(3, 2), (6, 7), (8, 13), (9, 15)], # 5
[(9, 14), (10, 16)], # 6
[(4, 2), (6, 5), (10, 15), (11, 17)], # 7
[(9, 10)], # [(5, 3), (9, 10), (13, 19)], # 8
[(6, 4), (10, 11)], # 9
[(6, 3), (9, 8)], # 10
[(10, 9)], # [(7, 4), (10, 9), (17, 20)], # 11
[(13, 14)], # 12
[(8, 5), (14, 15)], # 13
[(9, 6)], # [(9, 6), (13, 12), (15, 16)], # 14
[(9, 5), (10, 7), (14, 13), (16, 17)],# 15
[(10, 6)], # [(10, 6), (15, 14), (17, 18)], # 16
[(11, 7), (16, 15)], # 17
[(17, 16)], # 18
[(13, 8)], # 19
[(17, 11)], # 20
]
# コーナーペグ (0, 1, 12, 18, 19, 20)
corner = [
True, True, False, False, False,
False, False, False, False, False,
False, False, True, False, False,
False, False, False, True, True,
True
]
# 手順の表示
def print_move(xs):
from_, to_ = xs[0]
print(f'[{from_}, {to_}', end='')
prev = to_
for from_, to_ in xs[1:]:
if prev == from_:
print(f', {to_}', end='')
else:
print(f'][{from_}, {to_}', end='')
prev = to_
print(']')
# 反復深化 (下限値枝刈り法)
def dfs(board, jc, limit, lower, move):
global cnt
if jc + lower > limit: return
if len(move) == MAX_JUMP:
if board[HOLE]:
print_move(move)
cnt += 1
else:
for from_ in range(SIZE):
if not board[from_]: continue
for del_, to_ in jump_table_1[from_]:
if not board[del_] or board[to_]: continue
board[from_] = False
board[del_] = False
board[to_] = True
newjc = jc
if move[-1][1] != from_: newjc += 1
newlower = lower
if corner[from_]: newlower -= 1
if corner[to_]: newlower += 1
move.append((from_, to_))
dfs(board, newjc, limit, newlower, move)
move.pop()
board[from_] = True
board[del_] = True
board[to_] = False
def solver():
global cnt
cnt = 0
board = [True] * SIZE
# 初手を 14 -> 6 に限定
board[14] = False
board[9] = False
for i in range(7, MAX_JUMP + 1):
print(f'----- {i} -----')
dfs(board, 1, i, 6, [(14, 6)])
if cnt > 0: break
print(cnt)