M.Hiroi's Home Page / Memorandum 数学編

三角関数

●ピタゴラスの定理

図 1 : 直角三角形

ピタゴラスの定理は、平面幾何学において直角三角形 \(\triangle ABC\) の辺を \(a, b, c, \ (a + b \gt c)\) とすると、次式が成り立つという皆さんお馴染みの有名な定理です。

\( a^2 + b^2 = c^2 \)

「ピタゴラス数」または「ピタゴラスの三つ組数 (pythagoras triple)」は、上式を満たす自然数の組 (a, b, c) のことで、とくに a, b, c が互いに素であるとき、(a, b, c) を「原始ピタゴラス数」といいます。たとえば、(3, 4, 5), (5, 12, 13), (8, 15, 17) などがあります。

拙作のページ Puzzle DE Programming ピタゴラス数では、ピタゴラス数を求めるプログラムを Python で作成しています。興味のある方はお読みくださいませ。

●三角比と三角関数

図 1 の \(\triangle ABC\) で、\(\angle A\) を \(\theta\) とすると、角度 \(\theta\) と辺 \(a, b, c\) の長さの関係を次のように定めます。

\(\begin{array}{l} \sin \theta = \dfrac{c}{a} \\ \cos \theta = \dfrac{b}{a} \\ \tan \theta = \dfrac{c}{b} \end{array}\)

これを「三角比」といいます。角度 \(\theta\) の単位は度またはラジアンが用いられます。そして、sin, cos, tan を角度 \(\theta\) の関数としてとらえ、次の関数を加えたものを「三角関数」といいます。

\(\begin{array}{l} \sec \theta = \dfrac{a}{b} = \dfrac{1}{\cos \theta} \\ \csc \theta = \dfrac{a}{c} = \dfrac{1}{\sin \theta} \\ \cot \theta = \dfrac{b}{c} = \dfrac{1}{\tan \theta} \end{array}\)

呼び方は次のようになります。

sin (sine, サイン), 正弦
cos (cosine, コサイン), 余弦
tan (tangent, タンジェント), 正接
sec (secant), 正割
csc, cosec (cosecant), 余割
cot (cotangent), 余接

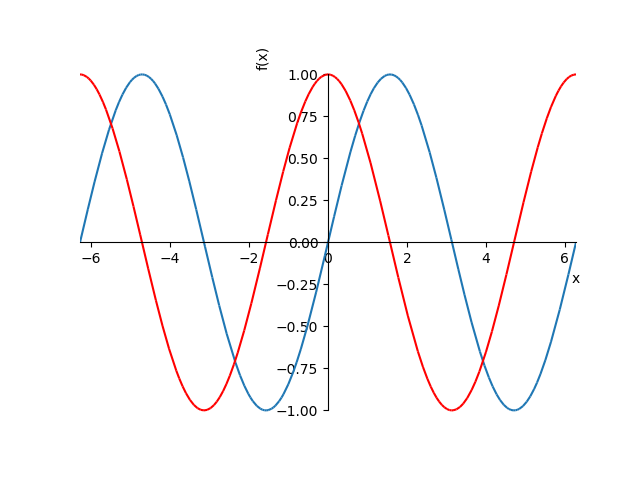
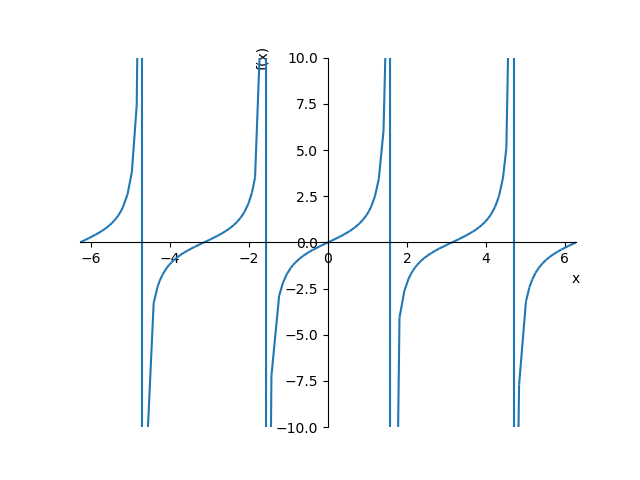
三角関数のグラフ

\(y = \sin x\), (cyan)
\(y = \cos x\), (red)

\(y = \tan x\)

負角の公式

\(\sin(-\theta) = - \sin \theta\)
\(\cos(-\theta) = \cos \theta\)
\(\tan(-\theta) = - \tan \theta\)

余角の公式

\(\sin\left(\dfrac{\pi}{2}-\theta\right) = \cos \theta\)
\(\cos\left(\dfrac{\pi}{2}-\theta\right) = \sin \theta\)
\(\tan\left(\dfrac{\pi}{2}-\theta\right) = -\dfrac{1}{\tan \theta}\)

補角の公式

\(\sin\left(\pi-\theta\right) = \sin \theta\)
\(\cos\left(\pi-\theta\right) = -\cos \theta\)
\(\tan\left(\pi-\theta\right) = -\tan \theta\)

●ピタゴラスの定理の証明

ピタゴラスの定理は三角比を使って簡単に証明することができます。図 1 の直角三角形 \(\triangle ABC\) の \(\angle C\) から辺 \(c\) に垂線を引き、交点を \(H\) とします。

\(\begin{eqnarray} c^2 &=& c \times (BH + HA) \\ &=& c \times (a \cos B + b \cos A) \\ &=& a (c \cos B) + b (c \cos A) \\ &=& a^2 + b^2 \end{eqnarray}\)

●余弦定理と正弦定理

図 2 : 三角形

図 2 の三角形 \(\triangle ABC\) の角を \(A, B, C\) とし、それに対応する辺の長さを \(a, b, c\) とすると、次の公式が成り立ちます。

第一余弦定理
\(a = b \cos C + c \cos B\)
\(b = c \cos A + a \cos C\)
\(c = a \cos B + b \cos A\)
第二余弦定理
\(a^2 = b^2 + c^2 - 2bc \cos A\)
\(b^2 = a^2 + c^2 - 2ac \cos B\)
\(c^2 = a^2 + b^2 - 2ab \cos C\)

第一余弦定理の証明は簡単です。最初の式では、\(\angle A\) から \(a\) に垂線を引いて、交点が \(H\) だとしましょう。\(BH = c \cos B, CH = b \cos C\) になるので、\(a = BH + CH = b \cos C + c \cos B\) が成立します。他の式も同様です。

第二余弦定理は第ー余弦定理を使うと簡単に証明できます。最初の式を証明します。

\(\begin{array}{l} a^2 - b^2 - c^2 \\ = a(b \cos C + c \cos B) -b(c \cos A + a \cos C) - c(a \cos B + b \cos A)\\ = ab \cos C + ac \cos B -bc \cos A - ab \cos C - ac \cos B - bc \cos A\\ = -2bc \cos A \end{array}\)

よって、\(a^2 = b^2 + c^2 - 2bc \cos A\)

他の式も同様です。

また、図 2 の三角形 \(\triangle ABC\) において、外接円の半径を \(R\) とすると、以下の公式が成り立ちます。

正弦定理
\(\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin A} = 2R\)

証明の概略を示します。辺 \(a\) を固定して \(\angle A\) を円周上で動かします。このとき、円周角の値は同じであることに注意してください。辺 \(b\) が直径になるように \(\angle A\) を動かすと、\(\angle C\) は直角になるので、辺 \(a\) の値は \(2R\sin A\) で求めることができます。つまり \(\dfrac{a}{\sin A} = 2R\) となることがわかります。他の辺と角でも同様です。

●三角関数の相互関係

\(\sin^2 \theta + \cos^2 \theta = 1\)
証明

\(\begin{eqnarray} \sin^2 \theta + \cos^2 \theta &=& \left(\frac{c}{a}\right)^2 + \left(\frac{b}{a}\right)^2 \\ &=& \frac{b^2 + c^2}{a^2} \\ &=& \frac{a^2}{a^2} = 1 \end{eqnarray}\)

\(\tan \theta = \dfrac{\sin \theta}{\cos \theta}\)
証明

\( \dfrac{\sin \theta}{\cos \theta} = \dfrac{c}{a} \times \dfrac{a}{b} = \dfrac{c}{b} = \tan \theta \)

\(1 + \dfrac{1}{\tan^2 \theta} = \dfrac{1}{\sin^2 \theta}\)
証明

\(\begin{eqnarray} 1 + \dfrac{1}{\tan^2 \theta} &=& 1 + \left(\dfrac{b}{c}\right)^2 \\ &=& \dfrac{c^2 + b^2}{c^2} \\ &=& \left(\dfrac{a}{c}\right)^2 = \dfrac{1}{\sin^2 \theta} \end{eqnarray}\)

\(1 + \tan^2 \theta = \dfrac{1}{\cos^2 \theta}\)
証明

\(\begin{eqnarray} 1 + \tan^2 \theta &=& 1 + \left(\dfrac{c}{b}\right)^2 \\ &=& \dfrac{c^2 + b^2}{b^2} \\ &=& \left(\dfrac{a}{b}\right)^2 = \dfrac{1}{\cos^2 \theta} \end{eqnarray}\)

●加法定理

\(\begin{array}{l} \sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ \tan(\alpha \pm \beta) = \dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \end{array}\)

余弦定理を使う証明が有名だと思いますが、オイラーの公式を使って三角関数を指数関数に変換し、指数法則を用いて加法定理を導くこともできます。ここでは \(\cos \alpha \cos \beta + \sin \alpha \sin \beta = \cos(\alpha-\beta)\) を証明します。

オイラーの公式 \(e^{i\theta} = \cos \theta + i \sin \theta\), (\(i\) は虚数単位)
負角の公式 \(\sin(-\theta) = -\sin \theta, \ \cos(-\theta) = \cos \theta \) より
\( \begin{eqnarray} e^{i(-\theta)} &=& \cos(-\theta) + i \sin(-\theta) \\ &=& \cos \theta - i \sin \theta \end{eqnarray} \)
\( \begin{array}{l} e^{i\theta} + e^{-i\theta} = 2 \cos \theta \\ \cos \theta = \dfrac{e^{i\theta} + e^{-i\theta}}{2} \\ e^{i\theta} - e^{-i\theta} = 2i \sin \theta \\ \sin \theta = \dfrac{e^{i\theta} - e^{-i\theta}}{2i} \end{array} \)

\(\begin{array}{l} \cos \alpha \cos \beta + \sin \alpha \sin \beta \\ = \dfrac{e^{i\alpha}+e^{-i\alpha}}{2} \cdot \dfrac{e^{i\beta}+e^{-i\beta}}{2} + \dfrac{e^{i\alpha}-e^{-i\alpha}}{2i} \cdot \dfrac{e^{i\beta}-e^{-i\beta}}{2i} \\ = \dfrac{1}{4}\left(e^{i(\alpha+\beta)} + e^{i(\alpha-\beta)} + e^{-i(\alpha-\beta)} + e^{-i(\alpha+\beta)} - e^{i(\alpha+\beta)} + e^{i(\alpha-\beta)} + e^{-i(\alpha-\beta)} - e^{-i(\alpha+\beta)} \right) \\ = \dfrac{2e^{i(\alpha-\beta)} + 2e^{-i(\alpha-\beta)}}{4} = \dfrac{e^{i(\alpha-\beta)} + e^{-i(\alpha-\beta)}}{2} = \cos(\alpha-\beta) \end{array}\)

●倍角と半角の公式

倍角の公式は加法定理で \(\beta = \alpha\) とすれば導くことができます。

\(\begin{array}{l} \sin 2\alpha = 2\sin \alpha \cos \alpha \\ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = 1 - 2 \sin^2 \alpha = 2 \cos^2 \alpha - 1\\ \tan 2\alpha = \dfrac{2 \tan \alpha}{1 - \tan^2 \alpha} \end{array}\)

半角の公式は、倍角の公式 \(\cos 2\alpha = 1 - 2 \sin^2 \alpha = 2 \cos^2 \alpha - 1\) で、\(\alpha\) を \(\frac{\alpha}{2}\) とすれば導くことができます。

\(\begin{array}{l} \sin^2 {\dfrac{\alpha}{2}} = \dfrac{1 - \cos \alpha}{2} \\ \cos^2 {\dfrac{\alpha}{2}} = \dfrac{1 + \cos \alpha}{2} \\ \tan^2 {\dfrac{\alpha}{2}} = \dfrac{1 - \cos \alpha}{1 + \cos \alpha} \end{array}\)

●和積と積和の公式

\(\begin{array}{l} \sin \alpha \cos \beta = \dfrac{1}{2}\left(\sin(\alpha + \beta) + \sin(\alpha - \beta)\right) \\ \cos \alpha \sin \beta = \dfrac{1}{2}\left(\sin(\alpha + \beta) - \sin(\alpha - \beta)\right) \\ \cos \alpha \cos \beta = \dfrac{1}{2}\left(\cos(\alpha + \beta) + \cos(\alpha - \beta)\right) \\ \sin \alpha \sin \beta = \dfrac{1}{2}\left(\cos(\alpha + \beta) - \cos(\alpha - \beta)\right) \\ \end{array}\)

積を和と差に直す公式は加法定理から導くことができます。一番上の公式を証明します。

\(\begin{array}{l} \sin(\alpha + \beta) + \sin(\alpha - \beta) \\ = \sin \alpha \cos \beta + \cos \alpha \sin \beta + \sin \alpha \cos \beta - \cos \alpha \sin \beta \\ = 2 \sin \alpha \cos \beta \end{array}\)
よって、\(\sin \alpha \cos \beta = \dfrac{1}{2}\left(\sin(\alpha + \beta) + \sin(\alpha - \beta)\right)\)

\(\begin{array}{l} \sin A + \sin B = 2 \sin \dfrac{A + B}{2} \cos \dfrac{A - B}{2} \\ \sin A - \sin B = 2 \cos \dfrac{A + B}{2} \sin \dfrac{A - B}{2} \\ \cos A + \cos B = 2 \cos \dfrac{A + B}{2} \cos \dfrac{A - B}{2} \\ \cos A - \cos B = -2 \sin \dfrac{A + B}{2} \sin \dfrac{A - B}{2} \end{array}\)

和と差を積に直す公式は、積を和と差に直す公式から導くことができます。一番上の公式を証明します。

\(\alpha + \beta = A, \ \alpha - \beta = B\) とすると、
\(\alpha = \dfrac{A + B}{2}, \ \beta = \dfrac{A - B}{2}\) となる

これを公式に代入すると
\(\begin{array}{l} \sin \alpha \cos \beta = \dfrac{1}{2}\left(\sin(\alpha + \beta) + \sin(\alpha - \beta)\right) \\ 2 \sin \dfrac{A + B}{2} \cos \dfrac{A - B}{2} = \sin A + \sin B \end{array}\)
となる

●三角関数の合成

\( a \sin \theta + b \cos \theta = \sqrt {a^2 + b^2} \sin(\theta + \alpha) \)

ただし
\(\begin{array}{l} \sin \alpha = \dfrac{b}{\sqrt{a^2+b^2}} \\ \cos \alpha = \dfrac{a}{\sqrt{a^2+b^2}} \\ \tan \alpha = \dfrac{b}{a} \end{array}\)

加法定理を使うと簡単に証明することができます。

\(\begin{eqnarray} \sqrt {a^2 + b^2} \sin(\theta + \alpha) &=& \sqrt {a^2 + b^2} \left(\sin \theta \cos \alpha + \cos \theta \sin \alpha \right) \\ &=& \sqrt {a^2 + b^2} \left(\sin \theta \dfrac{a}{\sqrt{a^2+b^2}} + \cos \theta \dfrac{b}{\sqrt{a^2+b^2}} \right) \\ &=& a \sin \theta + b \cos \theta \end{eqnarray}\)

●逆三角関数

三角関数の逆関数を「逆三角関数 (inverse trigonometric function)」といいます。

\(\begin{array}{ll} \arcsin x = w & \sin w = x \\ \arccos x = w & \cos w = x \\ \arctan x = w & \tan w = x \end{array}\)

\(\arcsin x\) は引数 x が与えられたとき \(\sin w = x\) となる角度 \(w\) を求めます。\(arcos x\) は \(\cos w = x\) となる \(w\) を、\(arctan x\) は \(\tan x = w\) となる \(w\) を求めます。逆三角関数は \(\sin^{-1} x, \cos^{-1} x, \tan^{-1} x\) と表記することもあります。

三角関数には周期性があるので、上式を満たす角度 \(w\) は無数に存在します。つまり、逆三角関数の返り値は無数にあることになりますが、通常は一つの値を返すように範囲を制限します。これを「主値」といいます。逆三角関数の主値を以下に示します。

\(\begin{array}{lll} \arcsin x = w & -1 \leqq x \lt 1 & -\pi/2 \leqq w \leqq \pi/2 \\ \arccos x = w & -1 \leqq x \lt 1 & 0 \leqq w \leqq \pi \\ \arctan x = w & x \in \mathbb{R} & -\pi/2 \leqq w \leqq \pi/2 \end{array}\)

プログラミング言語の場合、角度を求める関数 atan2 がライブラリ (数学関数) に用意されているのが一般的です。

atan2(y, x) => 角度 (ラジアン)

引数 x, y は実数です。atan2 は直交座標系においてベクトル (x, y) と x 軸との角度を求める関数です。複素平面で考えると、複素数 \(x + iy\) の偏角 \(\theta\) を求めることと同じです。\(\arcsin\) と \(\arccos\) は atan2 から求めることができます。

原点が中心で半径が 1 の円を考える
円周上の座標を (x, y) とし (x, y) - (0, 0) - (x, 0) の角度を \(\theta\) とする
三角関数の定義 \(\sin \theta = y, \ \cos \theta = x \ \) により

\( \begin{eqnarray} \arcsin y &=& \theta \\ &=& \mathrm{atan2}(y, x) \\ &=& \mathrm{atan2}\left(y, \sqrt{1 - y^2}\right) \\ \arccos x &=& \theta \\ &=& \mathrm{atan2}(y, x) \\ &=& \mathrm{atan2}\left(\sqrt{1 - x^2}, x\right) \end{eqnarray} \)

逆三角関数には次の関係が成り立ちます。

\(\begin{array}{l} \arcsin x = \arctan{\dfrac{x}{\sqrt{1 - x^2}}} \\ \arccos x = \dfrac{\pi}{2} - \arcsin x \end{array}\)

上式を使って \(\arcsin, \ \arccos\) を定義することもできます。