微分
●微分の定義
\(
f’(x) = \displaystyle \lim_{\varDelta x \to 0} \frac{f(x+\varDelta x) - f(x)}{\varDelta x}
\)
\(x\) の関数である \(f(x)\) について、上式の \(f'(x)\) を \(f(x)\) の導関数と呼びます。\(\varDelta x\) は \(x\) の小さな変化を表します。そして、導関数 \(f'(x)\) を求めることを \(f(x)\) を微分するといいます。関数を \(y = f(x)\) とする表記する場合は、導関数を \(\frac{dy}{dx}\)、あるいは \(y'\) と書きます。
\(f'(x)\) に特定の値を代入した \(f'(a)\) を微分係数といいます。\(x = a, \, \varDelta x = b - a\) とすると、左辺の分子・分母は \(\frac{f(b) - f(a)}{b - a}\) となるので、区間 [a, b] での平均変化率を表しています。左辺は \(\varDelta x \to 0\) の極限値を求めていますが、これは \(b \to a\) の極限値を求めることと同じです。つまり、\(f'(a)\) は \(x = a\) における \(f(x)\) の変化率 (接線の傾き) になります。
関数 \(f(x)\) が常に \(x\) で微分できるとは限りません。\(b \gt a \gt c\) において \(x = a\) で微分が可能であるためには、\(b \to a\) と \(c \to a\) の極限値が同じ値でなければなりません。つまり、\(a\) 点にプラス側から近づいたときと、マイナス側から近づいたときの傾斜が一致する必要があります。これを式で表すと次のようになります。
\(
\displaystyle \lim_{\varDelta x \to +0} \frac{f(a+\varDelta x) - f(x)}{\varDelta x} = \lim_{\varDelta x \to -0} \frac{f(a+\varDelta x) - f(x)}{\varDelta x}
\)
\(\varDelta x \to +0\) は正の値が 0 に近づく、\(\varDelta x \to -0\) は負の値が 0 に近づくという意味です。
簡単な例を示しましょう。
\(f(x) = x^2\) の導関数を求める
\(\begin{eqnarray} f'(x) &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{(x + \varDelta x)^2 - x^2}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{2x\cdot\varDelta x + {\varDelta x}^2}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} (2x + \varDelta x) = 2x \end{eqnarray}\)
\(\begin{eqnarray} f'(x) &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{(x + \varDelta x)^2 - x^2}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{2x\cdot\varDelta x + {\varDelta x}^2}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} (2x + \varDelta x) = 2x \end{eqnarray}\)
\(x^2\) を \(x\) で微分すると \(2x\) になります。これを \(\dfrac{d}{dx} x^2 = 2x\) と表記します。
絶対値関数 \(f(x) = |x|\) は、原点 \((x = 0)\) で微分不能です。
絶対値関数 \(f(x) = |x| = \begin{cases}
x & \mathrm{if} \ x \geqq 0 \\
-x & \mathrm{if} \ x \lt 0 \\
\end{cases}
\)
\(f(x)\) の導関数は
\(f'(x) = \begin{cases} 1 & \mathrm{if} \ x \gt 0 \\ -1 & \mathrm{if} \ x \lt 0 \\ \end{cases}\)
\(x = 0\) は微分可能ではないことの証明
\(\begin{eqnarray} f'(0+0) &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{f(0 + \varDelta x) - f(0)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{(0 + \varDelta x) - (0)}{\varDelta x} = 1 \\ f'(0-0) &=& \displaystyle \lim_{\varDelta x \to -0} \dfrac{f(0 + \varDelta x) - f(0)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{-(0 + \varDelta x) - -(0)}{\varDelta x} = -1 \end{eqnarray}\)
\(f'(0+0) \ne f'(0-0)\) なので \(x = 0\) は微分不能
\(f(x)\) の導関数は
\(f'(x) = \begin{cases} 1 & \mathrm{if} \ x \gt 0 \\ -1 & \mathrm{if} \ x \lt 0 \\ \end{cases}\)
\(x = 0\) は微分可能ではないことの証明
\(\begin{eqnarray} f'(0+0) &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{f(0 + \varDelta x) - f(0)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{(0 + \varDelta x) - (0)}{\varDelta x} = 1 \\ f'(0-0) &=& \displaystyle \lim_{\varDelta x \to -0} \dfrac{f(0 + \varDelta x) - f(0)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to +0} \dfrac{-(0 + \varDelta x) - -(0)}{\varDelta x} = -1 \end{eqnarray}\)
\(f'(0+0) \ne f'(0-0)\) なので \(x = 0\) は微分不能
\(f'(0+0)\) はプラス側から 0 に近づける、\(f'(0-0)\) はマイナス側から 0 に近づけるという意味です。
●基本関数の微分
\(\begin{array}{l}
y = f(x) & f'(x) \\
x^n & nx^{n-1} \\
e^x & e^x \\
a^x & (\log_e a)a^x \\
\log_e x & \dfrac{1}{x} \\
\sin x & \cos x \\
\cos x & - \sin x \\
\tan x & \sec^2 x \\
\sec x & \sec x \tan x \\
\csc x & - \csc x \cot x \\
\cot x & - \csc^2 x \\
\mathrm{Constant} & 0
\end{array}\)
\(\dfrac{d}{dx} x^n = nx^{n-1}\) の証明 (\(n\) は任意の正の整数)
\(\begin{eqnarray} \dfrac{d}{dx} x^n &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{(x + \varDelta x)^n - x^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{x^n + {}_n \mathrm{C}_1 x^{n-1} \varDelta x + {}_n \mathrm{C}_2 x^{n-2} {\varDelta x}^2 + \cdots + {\varDelta x}^n - x^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{{}_n \mathrm{C}_1 x^{n-1} \varDelta x + {}_n \mathrm{C}_2 x^{n-2} {\varDelta x}^2 + \cdots + {\varDelta x}^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} {}_n\mathrm{C}_1 x^{n-1} + {}_n\mathrm{C}_2 x^{n-2} {\varDelta x} + \cdots + {\varDelta x}^{n-1} \\ &=& {}_n \mathrm{C}_1 x^{n-1} = nx^{n-1} \end{eqnarray}\)
\(\begin{eqnarray} \dfrac{d}{dx} x^n &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{(x + \varDelta x)^n - x^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{x^n + {}_n \mathrm{C}_1 x^{n-1} \varDelta x + {}_n \mathrm{C}_2 x^{n-2} {\varDelta x}^2 + \cdots + {\varDelta x}^n - x^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{{}_n \mathrm{C}_1 x^{n-1} \varDelta x + {}_n \mathrm{C}_2 x^{n-2} {\varDelta x}^2 + \cdots + {\varDelta x}^n}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} {}_n\mathrm{C}_1 x^{n-1} + {}_n\mathrm{C}_2 x^{n-2} {\varDelta x} + \cdots + {\varDelta x}^{n-1} \\ &=& {}_n \mathrm{C}_1 x^{n-1} = nx^{n-1} \end{eqnarray}\)
なお、\(\dfrac{d}{dx} x^n = nx^{n-1}\) は \(n\) が任意の実数でも成立します。証明はあとで (対数微分法) で行うことにしましょう。
ネイピア数と \(\dfrac{d}{dx} e^x = e^x\) の証明
\( \dfrac{d}{dx} e^x = \displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{x + \varDelta x} - e^x}{\varDelta x} = e^x \displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{\varDelta x} - 1}{\varDelta x} \\ \)
式 \(\displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{\varDelta x} - 1}{\varDelta x} = 1\) を満たす \(e\) を「ネイピア数」という (ネイピア数は超越数で値は \(e = 2.7182818284\ldots\))
ネイピア数の定義は他にもいくつかある
\(\begin{array}{l} \displaystyle \lim_{n \to 0} (1 + n)^{\frac{1}{n}} = e \\ \displaystyle \lim_{n \to \infty} \left(1 + \dfrac{1}{n}\right)^n = e \end{array}\)
よって、\(\dfrac{d}{dx} e^x = e^x\) を得る
\( \dfrac{d}{dx} e^x = \displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{x + \varDelta x} - e^x}{\varDelta x} = e^x \displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{\varDelta x} - 1}{\varDelta x} \\ \)
式 \(\displaystyle \lim_{\varDelta x \to 0} \dfrac{e^{\varDelta x} - 1}{\varDelta x} = 1\) を満たす \(e\) を「ネイピア数」という (ネイピア数は超越数で値は \(e = 2.7182818284\ldots\))
ネイピア数の定義は他にもいくつかある
\(\begin{array}{l} \displaystyle \lim_{n \to 0} (1 + n)^{\frac{1}{n}} = e \\ \displaystyle \lim_{n \to \infty} \left(1 + \dfrac{1}{n}\right)^n = e \end{array}\)
よって、\(\dfrac{d}{dx} e^x = e^x\) を得る
Python では、モジュール math にネイピア数 e が定義されています。
>>> import math >>> math.e 2.718281828459045 >>> (math.e**(1e-2) - 1) / 1e-2 1.005016708416795 >>> (math.e**(1e-4) - 1) / 1e-4 1.000050001667141 >>> (math.e**(1e-8) - 1) / 1e-8 0.999999993922529 >>> (1 + 1e-2)**(1/1e-2) 2.7048138294215285 >>> (1 + 1e-4)**(1/1e-4) 2.7181459268249255 >>> (1 + 1e-8)**(1/1e-8) 2.7182817983473577 >>> (1 + 1 / 1e2)**1e2 2.7048138294215285 >>> (1 + 1 / 1e4)**1e4 2.7181459268249255 >>> (1 + 1 / 1e8)**1e8 2.7182817983473577
\(\dfrac{d}{dx} \log_e x = \dfrac{1}{x}\) の証明
\(\begin{eqnarray} \dfrac{d}{dx} \log_e x &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{\log_e (x + \varDelta x) - \log_e x}{\varDelta x} = \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{\varDelta x} \log_e \dfrac{x + \varDelta x}{x}\\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{x} \dfrac{x}{\varDelta x} \log_e \left(1 + \dfrac{\varDelta x}{x}\right) = \dfrac{1}{x} \displaystyle \lim_{\varDelta x \to 0} \log_e \left(1 + \dfrac{\varDelta x}{x}\right)^{\frac{x}{\varDelta x}}\\ \end{eqnarray}\)
\(\dfrac{\varDelta x}{x} = k\) とおくと、\(\varDelta x \to 0\) のとき \(k \to 0\) だから
\( \dfrac{d}{dx} \log_e x = \dfrac{1}{x} \displaystyle \lim_{k \to 0} \log_e (1 + k)^{\frac{1}{k}} \)
ここで \( \displaystyle \lim_{k \to 0} (1 + k)^{\frac{1}{k}} = e \) なので \(\dfrac{d}{dx} \log_e x = \dfrac{1}{x}\log_e e = \dfrac{1}{x}\) となる
\(\begin{eqnarray} \dfrac{d}{dx} \log_e x &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{\log_e (x + \varDelta x) - \log_e x}{\varDelta x} = \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{\varDelta x} \log_e \dfrac{x + \varDelta x}{x}\\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{x} \dfrac{x}{\varDelta x} \log_e \left(1 + \dfrac{\varDelta x}{x}\right) = \dfrac{1}{x} \displaystyle \lim_{\varDelta x \to 0} \log_e \left(1 + \dfrac{\varDelta x}{x}\right)^{\frac{x}{\varDelta x}}\\ \end{eqnarray}\)
\(\dfrac{\varDelta x}{x} = k\) とおくと、\(\varDelta x \to 0\) のとき \(k \to 0\) だから
\( \dfrac{d}{dx} \log_e x = \dfrac{1}{x} \displaystyle \lim_{k \to 0} \log_e (1 + k)^{\frac{1}{k}} \)
ここで \( \displaystyle \lim_{k \to 0} (1 + k)^{\frac{1}{k}} = e \) なので \(\dfrac{d}{dx} \log_e x = \dfrac{1}{x}\log_e e = \dfrac{1}{x}\) となる
\(\dfrac{d}{dx} \sin x = \cos x\) の証明
\(\begin{eqnarray} \dfrac{d}{dx} \sin x &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{\sin (x + \varDelta x) - \sin x}{\varDelta x} = \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{\varDelta x} 2 \cos\left(\dfrac{2x+\varDelta x}{2}\right)\sin\left(\dfrac{\varDelta x}{2}\right) \\ &=& \displaystyle \lim_{\varDelta x \to 0} \cos\left(x + \dfrac{\varDelta x}{2}\right)\dfrac{\sin \dfrac{\varDelta x}{2}}{\dfrac{\varDelta x}{2}} \end{eqnarray}\)
三角関数の極限値
\(\begin{array}{ll} 1. & \displaystyle \lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} = 1 \\ 2. & \displaystyle \lim_{\theta \to 0} \dfrac{1 - \cos \theta}{\theta^2} = \dfrac{1}{2} \\ 3. & \displaystyle \lim_{\theta \to 0} \dfrac{\tan \theta}{\theta} = 1 \\ \end{array}\)
式 1 により、 \( \dfrac{d}{dx} \sin x = \displaystyle \lim_{\varDelta x \to 0} \cos\left(x + \dfrac{\varDelta x}{2}\right) \cdot 1 = \cos x \) を得る
\(\begin{eqnarray} \dfrac{d}{dx} \sin x &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{\sin (x + \varDelta x) - \sin x}{\varDelta x} = \displaystyle \lim_{\varDelta x \to 0} \dfrac{1}{\varDelta x} 2 \cos\left(\dfrac{2x+\varDelta x}{2}\right)\sin\left(\dfrac{\varDelta x}{2}\right) \\ &=& \displaystyle \lim_{\varDelta x \to 0} \cos\left(x + \dfrac{\varDelta x}{2}\right)\dfrac{\sin \dfrac{\varDelta x}{2}}{\dfrac{\varDelta x}{2}} \end{eqnarray}\)
三角関数の極限値
\(\begin{array}{ll} 1. & \displaystyle \lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} = 1 \\ 2. & \displaystyle \lim_{\theta \to 0} \dfrac{1 - \cos \theta}{\theta^2} = \dfrac{1}{2} \\ 3. & \displaystyle \lim_{\theta \to 0} \dfrac{\tan \theta}{\theta} = 1 \\ \end{array}\)
式 1 により、 \( \dfrac{d}{dx} \sin x = \displaystyle \lim_{\varDelta x \to 0} \cos\left(x + \dfrac{\varDelta x}{2}\right) \cdot 1 = \cos x \) を得る
Python の場合、モジュール math に三角関数 sin(), cos(), tan() が定義されています。
>>> math.sin(1e-2) / 1e-2 0.9999833334166665 >>> math.sin(1e-4) / 1e-4 0.9999999983333334 >>> math.sin(1e-8) / 1e-8 1.0 >>> (1 - math.cos(1e-2)) / (1e-2)**2 0.4999958333473664 >>> (1 - math.cos(1e-4)) / (1e-4)**2 0.4999999969612645 >>> math.tan(1e-2) / 1e-2 1.0000333346667207 >>> math.tan(1e-4) / 1e-4 1.0000000033333334 >>> math.tan(1e-8) / 1e-8 1.0
●関数の和・差・積・商の微分
関数 \(f(x), g(x)\), 定数 \(c\) とすると、\(f(x), g(x)\) が微分可能なとき以下の公式が成り立ちます。
- \((cf(x))' = cf'(x)\)
- \((f(x) \pm g(x))' = f'(x) \pm g'(x)\)
- \((f(x)g(x))' = g(x)f'(x) + f(x)g'(x)\)
- \(\left(\dfrac{f(x)}{g(x)}\right)' = \dfrac{g(x)f'(x) - f(x)g'(x)}{g^2(x)}\)
公式 1, 2 の証明は割愛させていただきます。公式 3 は微分の定義から導くことができます。
公式 3 の証明
\(\begin{eqnarray} (f(x)g(x))' &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)g(x + \varDelta x) - f(x)g(x)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)g(x + \varDelta x) + f(x + \varDelta x)g(x)- f(x + \varDelta x)g(x) - f(x)g(x)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)(g(x + \varDelta x) - g(x)) + g(x)(f(x + \varDelta x) - f(x))}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} f(x + \varDelta x)\dfrac{g(x + \varDelta x) - g(x)}{\varDelta x} + \lim_{\varDelta x \to 0} g(x)\dfrac{f(x + \varDelta x) - f(x)}{\varDelta x} \\ &=& f(x)g'(x) + g(x)f'(x) \end{eqnarray}\)
\(\begin{eqnarray} (f(x)g(x))' &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)g(x + \varDelta x) - f(x)g(x)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)g(x + \varDelta x) + f(x + \varDelta x)g(x)- f(x + \varDelta x)g(x) - f(x)g(x)}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(x + \varDelta x)(g(x + \varDelta x) - g(x)) + g(x)(f(x + \varDelta x) - f(x))}{\varDelta x} \\ &=& \displaystyle \lim_{\varDelta x \to 0} f(x + \varDelta x)\dfrac{g(x + \varDelta x) - g(x)}{\varDelta x} + \lim_{\varDelta x \to 0} g(x)\dfrac{f(x + \varDelta x) - f(x)}{\varDelta x} \\ &=& f(x)g'(x) + g(x)f'(x) \end{eqnarray}\)
公式 4 も同様に証明できますが、対数微分法を使ったほうが簡単です。これもあとで証明することにしましょう。
●合成関数の微分
関数 \(f(x)\) と \(g(x)\) を合成して新しい関数 \(y\) を作ることを考えてみましょう。関数 \(y\) を次のように定義します。
\(y = f(u), u = g(x)\) のとき、後の式を前の式に代入すると
\( y = f( g( x ) )\)
となる
\( y = f( g( x ) )\)
となる
これを合成関数といいます。たとえば、\(f(x) = 2x + 1, g(x) = x^2 + 3x\) とすると、\(y\) は次のようになります。
\(\begin{eqnarray}
y &=& f( g( x ) ) \\
&=& 2(x^2 + 3x) + 1 \\
&=& 2x^2 + 6x + 1
\end{eqnarray}\)
一般に、\(y = f(u)\) が \(u\) の関数として微分可能で、\(u = g(x)\) が \(x\) の関数として微分可能であれば、合成関数 \(y = f(g(x))\) も \(x\) の関数として微分可能であり、以下の公式が成り立ちます。
\(\dfrac{dy}{dx} = f'(g(x)) g'(x)\)
\(y = f(u),\ u = g(x)\) とすると
\( \dfrac {dy}{dx} = \dfrac {dy}{du} \times \dfrac {du}{dx} \)
\(y = f(u),\ u = g(x)\) とすると
\( \dfrac {dy}{dx} = \dfrac {dy}{du} \times \dfrac {du}{dx} \)
\(f(x) = 2x + 1, g(x) = x^2 + 3x\) の場合、\(f'(x) = 2, \ g'(x) = 2x + 3\) なので、\(y' = f'(g(x))g'(x) = 2(2x + 3) = 4 x + 6\) になります。これは合成関数 \(y = 2x^2 + 6x + 1\) を微分した \(y' = 4 x + 6\) と一致します。
証明の概略
\( \dfrac{d}{dx} f(g(x)) = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x + \varDelta x)) - f(g(x))}{\varDelta x} \)
微分の定義式の分子と分母に \(g(x + \varDelta x) - g(x)\) を掛け算する
(ただし、\(g(x + \varDelta x) \ne g(x)\) であること)
\( = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x + \varDelta x)) - f(g(x))}{g(x + \varDelta x) - g(x)} \cdot \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} \)
次に、\(g(x + \varDelta x) - g(x) = \varDelta u\) とおくと、\(g(x + \varDelta x) = g(x) + \varDelta u\) になるので、以下の式を得る
\( = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x) + \varDelta u) - f(g(x))}{\varDelta u} \cdot \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} \)
\(\varDelta x \to 0\) のとき \(\varDelta u \to 0\) になるので、以下の式を得る
\( \dfrac{d}{dx} f(g(x)) = \displaystyle \lim_{\varDelta u \to 0} \dfrac{f(g(x) + \varDelta u) - f(g(x))}{\varDelta u} \cdot \displaystyle \lim_{\varDelta x \to 0} \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} = f'(g(x)) g'(x) \)
\( \dfrac{d}{dx} f(g(x)) = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x + \varDelta x)) - f(g(x))}{\varDelta x} \)
微分の定義式の分子と分母に \(g(x + \varDelta x) - g(x)\) を掛け算する
(ただし、\(g(x + \varDelta x) \ne g(x)\) であること)
\( = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x + \varDelta x)) - f(g(x))}{g(x + \varDelta x) - g(x)} \cdot \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} \)
次に、\(g(x + \varDelta x) - g(x) = \varDelta u\) とおくと、\(g(x + \varDelta x) = g(x) + \varDelta u\) になるので、以下の式を得る
\( = \displaystyle \lim_{\varDelta x \to 0} \dfrac{f(g(x) + \varDelta u) - f(g(x))}{\varDelta u} \cdot \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} \)
\(\varDelta x \to 0\) のとき \(\varDelta u \to 0\) になるので、以下の式を得る
\( \dfrac{d}{dx} f(g(x)) = \displaystyle \lim_{\varDelta u \to 0} \dfrac{f(g(x) + \varDelta u) - f(g(x))}{\varDelta u} \cdot \displaystyle \lim_{\varDelta x \to 0} \dfrac{g(x + \varDelta x)- g(x)}{\varDelta x} = f'(g(x)) g'(x) \)
●対数微分法
対数微分法は両辺の対数をとってから微分する方法です。対数をとるとき、関数 \(\log_e x\) の定義域は \(x \gt 0\) であることに注意してください。簡単な例を示しましょう。
\(y = a^x, \ (a \gt 0, a \ne 1)\) を微分する場合、両辺の値は正になるので、対数をとることができる
\(\log_e y = x \log_e a\)
両辺を \(x\) で微分する。左辺は合成関数の公式により \(\dfrac{y'}{y}\) になる
\(\begin{array}{l} \dfrac{y'}{y} = \log_e a \\ y' = y \log_e a = a^x \log_e a \end{array}\)
\(\log_e y = x \log_e a\)
両辺を \(x\) で微分する。左辺は合成関数の公式により \(\dfrac{y'}{y}\) になる
\(\begin{array}{l} \dfrac{y'}{y} = \log_e a \\ y' = y \log_e a = a^x \log_e a \end{array}\)
\(y = x^n, \ (x \gt 0, x \in \mathbb{R})\) を微分する場合、両辺の対数をとる
\(log_e y = n \log_e x\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{n}{x} \\ y' = \dfrac{ny}{x} = n x^{n - 1} \end{array}\)
\(log_e y = n \log_e x\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{n}{x} \\ y' = \dfrac{ny}{x} = n x^{n - 1} \end{array}\)
\(y = f(x)g(x), \ (f(x) \gt 0, g(x) \gt 0)\) を微分する場合、両辺の対数をとる
\(\log_e y = \log_e (f(x)g(x)) = \log_e f(x) + \log_e g(x)\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{f'(x)}{f(x)} + \dfrac{g'(x)}{g(x)} \\ y' = f(x)g(x) \left(\dfrac{f'(x)}{f(x)} + \dfrac{g'(x)}{g(x)}\right) = g(x)f'(x) + f(x)g'(x) \end{array}\)
\(\log_e y = \log_e (f(x)g(x)) = \log_e f(x) + \log_e g(x)\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{f'(x)}{f(x)} + \dfrac{g'(x)}{g(x)} \\ y' = f(x)g(x) \left(\dfrac{f'(x)}{f(x)} + \dfrac{g'(x)}{g(x)}\right) = g(x)f'(x) + f(x)g'(x) \end{array}\)
\(y = \dfrac{f(x)}{g(x)}, \ (f(x) \gt 0, g(x) \gt 0)\) を微分する場合、両辺の対数をとる
\(\log_e y = \log_e \left(\dfrac{f(x)}{g(x)}\right) = \log_e f(x) - \log_e g(x)\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{f'(x)}{f(x)} - \dfrac{g'(x)}{g(x)} \\ y' = \dfrac{f(x)}{g(x)} \left(\dfrac{f'(x)}{f(x)} - \dfrac{g'(x)}{g(x)}\right) = \dfrac{g(x)f'(x) - f(x)g'(x)}{g^2(x)} \end{array}\)
\(\log_e y = \log_e \left(\dfrac{f(x)}{g(x)}\right) = \log_e f(x) - \log_e g(x)\)
両辺を \(x\) で微分する。
\(\begin{array}{l} \dfrac{y'}{y} = \dfrac{f'(x)}{f(x)} - \dfrac{g'(x)}{g(x)} \\ y' = \dfrac{f(x)}{g(x)} \left(\dfrac{f'(x)}{f(x)} - \dfrac{g'(x)}{g(x)}\right) = \dfrac{g(x)f'(x) - f(x)g'(x)}{g^2(x)} \end{array}\)
●逆関数の微分
関数 \(y = f(x)\) において、\(x\) と \(y\) が 1 対 1 の対応になっている場合、\(y\) から \(x\) を求める関数 \(x = g(y)\) を考えることができます。このような関数 \(g\) を「逆関数」といい、一般的には \(y = f^{-1}(x)\) と表記します。逆関数の微分は以下の式が成り立ちます。
微分可能な関数 \(y = f(x)\) と逆関数 \(y = g(x)\) が存在するとき
\(g'(x) = \dfrac{1}{f'(y)}\) または \(\dfrac{dy}{dx} = \dfrac{1}{\frac{dx}{dy}}\)
\(g'(x) = \dfrac{1}{f'(y)}\) または \(\dfrac{dy}{dx} = \dfrac{1}{\frac{dx}{dy}}\)
証明
関数 \(y = f(x)\) において、その逆関数を \(y = g(x)\) とすると、逆関数の定義より \(x = f(y)\) となる
両辺を \(x\) で微分すると、合成関数の公式により
\(\begin{array}{l} 1 = f'(y) \cdot y' \\ y' = \dfrac{1}{f'(y)} \\ g'(x) = \dfrac{1}{f'(y)} \end{array}\)
\(g'(x) = \dfrac{dy}{dx}, f'(y) = \dfrac{dx}{dy}\) より \(\dfrac{dy}{dx} = \dfrac{1}{\frac{dx}{dy}}\)
関数 \(y = f(x)\) において、その逆関数を \(y = g(x)\) とすると、逆関数の定義より \(x = f(y)\) となる
両辺を \(x\) で微分すると、合成関数の公式により
\(\begin{array}{l} 1 = f'(y) \cdot y' \\ y' = \dfrac{1}{f'(y)} \\ g'(x) = \dfrac{1}{f'(y)} \end{array}\)
\(g'(x) = \dfrac{dy}{dx}, f'(y) = \dfrac{dx}{dy}\) より \(\dfrac{dy}{dx} = \dfrac{1}{\frac{dx}{dy}}\)
簡単な例を示します。
\(y = a^x, (a \gt 0, a \ne 1)\) を微分する。
逆関数は \(x = \log_a y = \dfrac{\log_e y}{\log_e a}\) となる
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \dfrac{1}{y \log_e a}\) となる
逆関数の微分公式により \(\dfrac{dy}{dx} = y \log_e a = a^x \log_e a\) を得る
逆関数は \(x = \log_a y = \dfrac{\log_e y}{\log_e a}\) となる
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \dfrac{1}{y \log_e a}\) となる
逆関数の微分公式により \(\dfrac{dy}{dx} = y \log_e a = a^x \log_e a\) を得る
逆三角関数 \(y = \arcsin x\) を微分する
逆関数の定義により \(x = \sin y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \cos y\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = \dfrac{1}{\cos y} = \dfrac{1}{\sqrt {1 - \sin^2 y}} = \dfrac{1}{\sqrt {1 - x^2}}\)
逆関数の定義により \(x = \sin y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \cos y\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = \dfrac{1}{\cos y} = \dfrac{1}{\sqrt {1 - \sin^2 y}} = \dfrac{1}{\sqrt {1 - x^2}}\)
逆三角関数 \(y = \arccos x\) を微分する
逆関数の定義により \(x = \cos y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = -\sin y\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = -\dfrac{1}{\sin y} = -\dfrac{1}{\sqrt {1 - \cos^2 y}} = -\dfrac{1}{\sqrt {1 - x^2}}\)
逆関数の定義により \(x = \cos y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = -\sin y\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = -\dfrac{1}{\sin y} = -\dfrac{1}{\sqrt {1 - \cos^2 y}} = -\dfrac{1}{\sqrt {1 - x^2}}\)
逆三角関数 \(y = \arctan x\) を微分する
逆関数の定義により \(x = \tan y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \dfrac{1}{\cos^2 y}\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = \cos^2 y = \dfrac{1}{1 + \tan^2 y} = \dfrac{1}{1 + x^2}\)
逆関数の定義により \(x = \tan y\)
これを \(y\) で微分すると \(\dfrac{dx}{dy} = \dfrac{1}{\cos^2 y}\)
逆関数の微分公式により
\(\dfrac{dy}{dx} = \cos^2 y = \dfrac{1}{1 + \tan^2 y} = \dfrac{1}{1 + x^2}\)
●平均値の定理
関数 \(y = f(x)\) が区間 [a, b] で連続、区間 (a, b) で微分可能であるならば
\(\dfrac{f(b) - f(a)}{b - a} = f'(c) \quad (a \lt c \lt b)\)
上式を満たす c が少なくとも 1 つは存在します。これを「平均値の定理」といいます。
公式の左辺は座標 \((a, f(a)), (b, f(b))\) を結ぶ直線の傾きを表します。右辺はその傾きと同じ値の微分係数が \((a, f(a))\) から \((b, f(b))\) までの \(f(x)\) の曲線上に少なくとも 1 つは存在することを表します。たとえば、\(y = x^2\) において、区間 (1, 1), (2, 4) の傾きは 3 になります。\(y\) を微分すると \(y' = 2x\) になるので、\(y'\) が 3 となる \(x\) は 1.5 になります。確かに区間 [1, 2] の間に存在していますね。
平均値の定理は「ロルの定理」を使うと簡単に証明することができます。
[ロルの定理]
区間 [a, b] で連続、区間 (a, b) で微分可能、\(f(a) = f(b)\) なる関数 \(f(x)\) について
\(f'(c) = 0 \quad (a \lt c \lt b)\)
を満たす c が存在する
区間 [a, b] で連続、区間 (a, b) で微分可能、\(f(a) = f(b)\) なる関数 \(f(x)\) について
\(f'(c) = 0 \quad (a \lt c \lt b)\)
を満たす c が存在する
たとえば、\(f(x) = x^2\) において、\(a = -1, b = 1\) とすると \(f(a) = f(b) = 1\) になります。このとき、\(c = 0\) で微分係数が 0 になるので、ロルの定理が正しいことがわかります。
ここではロルの定理の証明は割愛させていただき、ロルの定理が正しいことを認めて、平均値の定理を証明してみましょう。
証明
関数 \(g(x) = f(x) + \alpha x\) を考えて、\(g(a) = g(b)\) となる \(\alpha\) を求める
\(\begin{array}{l} f(a) + \alpha a = f(b) + \alpha b \\ \alpha (a - b) = f(b) - f(a) \\ \alpha = -\dfrac{f(b) - f(a)}{b - a} \end{array}\)
関数 \(g(x) = f(x) - \dfrac{f(b) - f(a)}{b - a}x\) が \(g(a) = g(b)\) を満たすので、ロルの定理により
\(g'(c) = 0 \quad (a \lt c \lt b)\)
となる c が存在する。\(g(x)\) を微分すると \(g'(x) = f'(x) - \dfrac{f(b) - f(a)}{b - a}\) になるので
\(g'(c) = f'(c) - \dfrac{f(b) - f(a)}{b - a} = 0\) となり、平均値の定理を得る
関数 \(g(x) = f(x) + \alpha x\) を考えて、\(g(a) = g(b)\) となる \(\alpha\) を求める
\(\begin{array}{l} f(a) + \alpha a = f(b) + \alpha b \\ \alpha (a - b) = f(b) - f(a) \\ \alpha = -\dfrac{f(b) - f(a)}{b - a} \end{array}\)
関数 \(g(x) = f(x) - \dfrac{f(b) - f(a)}{b - a}x\) が \(g(a) = g(b)\) を満たすので、ロルの定理により
\(g'(c) = 0 \quad (a \lt c \lt b)\)
となる c が存在する。\(g(x)\) を微分すると \(g'(x) = f'(x) - \dfrac{f(b) - f(a)}{b - a}\) になるので
\(g'(c) = f'(c) - \dfrac{f(b) - f(a)}{b - a} = 0\) となり、平均値の定理を得る
●極大値と極小値
関数 \(y = f(x)\) の局所的な最大値を「極大値」、局所的な最小値を「極小値」といいます。二つあわせて「極値」といい、関数の極値を求める問題を「極値問題」といいます。極値は次に示すように微分係数で判定することができます。
関数 \(y = f(x)\) において \(f'(a) = 0\) のとき、
\(f''(a) \gt 0\) なら、\(f(a)\) は極小値
\(f''(a) \lt 0\) なら、\(f(a)\) は極大値
\(f''(a) \gt 0\) なら、\(f(a)\) は極小値
\(f''(a) \lt 0\) なら、\(f(a)\) は極大値
ここで \(f''(x)\) は \(f(x)\) を \(x\) で 2 回微分した関数 \(\dfrac{d^2}{dx^2} f(x)\) のことで、\(f''(a)\) は \(f''(x)\) の \(x\) に a を代入した値のことです。
簡単な例を示しましょう。
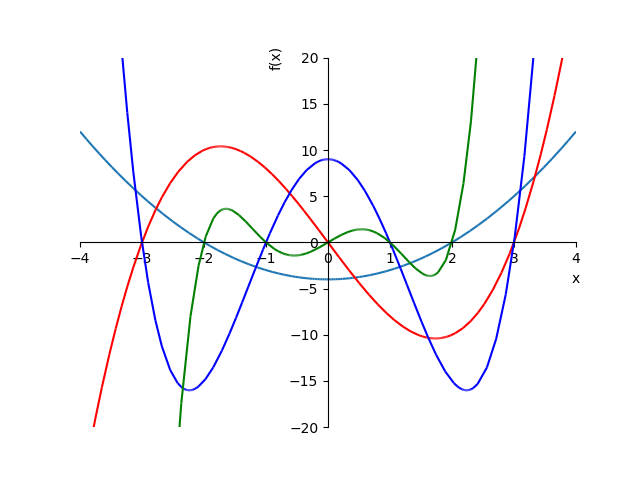
- \(f(x) = x^2 - 4\), (cyan)
- \(f(x) = x^3 - 9x\), (red)
- \(f(x) = x^4 - 10x^2 + 9\), (blue)
- \(f(x) = x^5 - 5x^3 + 4x\), (green)
- \(f'(x) = 2x, f''(x) = 2\) より \(f(0) = -4\) は極小値
- \(f'(x) = 3x^2 - 9, f''(x) = 6x\) より
- \(x = \pm \sqrt 3\) で極値
- \(x = \sqrt 3\) で極小値 -10.392304845413264
- \(x = -\sqrt 3\) で極大値 10.392304845413264
- \(f'(x) = 4x^3 - 20x, f''(x) = 12x^2 - 20\) より
- \(x = 0, \pm \sqrt 5\) で極値
- \(x = 0\) で極大値 9
- \(x \pm \sqrt 5\) で極小値 -16
- \(f'(x) = 5x^4 -15x^2 + 4, f''(x) = 20x^3 - 30x\) より
- SymPy で \(f'(x) = 0\) の解を求めると
- \(- \sqrt{\frac{3}{2} - \frac{\sqrt{145}}{10}}, \sqrt{\frac{3}{2} - \frac{\sqrt{145}}{10}}, - \sqrt{\frac{\sqrt{145}}{10} + \frac{3}{2}}, \sqrt{\frac{\sqrt{145}}{10} + \frac{3}{2}}\)
- \(x = \pm 0.5439122559023379, \pm 1.6444328681582685\) が極値になる
- \(x = 0.5439122559023379\) で極大値 1.4186966255829239
- \(x = -0.5439122559023379\) で極小値 -1.4186966255829239
- \(x = 1.6444328681582685\) で極小値 -3.6314322084488406
- \(x = -1.6444328681582685\) で極大値 3.6314322084488406