積分
●積分の定義
- \(\dfrac{d}{dx} F(x) = f(x)\)
- \(\displaystyle \int f(x)\,dx = F(x)\)
二つの関数 \(F(x)\) と \(f(x)\) の間に式 1 の関係があるとき、\(f(x)\) から \(F(x)\) を求める操作を「積分」といい、式 2 のように書きます。このとき、\(F(x)\) を「原始関数」と呼びます。
積分には「定積分」と「不定積分」の二種類あり、式 2 は不定積分を表しています。定数 を \(C\) とすると、\(C\) を微分すれば 0 になるので、以下の式が成り立ちます。
\(\dfrac{d}{dx}(F(x) + C) = f(x)\)
したがって、式 2 は以下のように書くことができます。
\(
\displaystyle \int f(x)\,dx = F(x) + C
\)
\(C\) は任意に選べる定数ですから、原始関数は無数に存在することになり、一義的に定めることはできません。それゆえに、式 2 の操作を不定積分といい、\(C\) を積分定数といいます。積分定数は省略されることもあります。
●基本関数の積分
\(\begin{array}{ll}
f(x) & F(x) \\
x^n & \dfrac{1}{n + 1}x^{n + 1} \quad (n \ne -1)\\
\dfrac{1}{x} & \log_e |x| \\
e^x & e^x \\
a^x & \dfrac{a^x}{\log_e a} \quad (a \gt 0, \ a \ne 1) \\
\sin x & - \cos x \\
\cos x & \sin x \\
\tan x & - \log_e |\cos x| \\
\cot x & \log_e |\sin x| \\
\sec^2 x & \tan x \\
\csc^2 x & - \cot x \\
\end{array}\)
右の関数 \(F(x)\) を微分すると左の関数 \(f(x)\) になります。
●基本的な積分の公式
関数の定数倍、和と差の積分公式を示します。
\(\begin{array}{l}
\displaystyle \int k f(x) \, dx = k \int f(x) \, dx \\
\displaystyle \int (f(x) \pm g(x)) \, dx = \int f(x) \, dx \pm \int g(x) \, dx \\
\end{array}\)
(\(k\) は定数)
(\(k\) は定数)
また、関数の積の微分公式から以下の公式を導くことができます。
微分公式 \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\) の両辺を積分する
\( f(x) g(x) = \displaystyle \int f'(x) g(x) \, dx + \int f(x) g'(x) \, dx \)
移項すると
\( \displaystyle \int f(x) g'(x) \, dx = f(x) g(x) - \int f'(x) g(x) \, dx \)
\( f(x) g(x) = \displaystyle \int f'(x) g(x) \, dx + \int f(x) g'(x) \, dx \)
移項すると
\( \displaystyle \int f(x) g'(x) \, dx = f(x) g(x) - \int f'(x) g(x) \, dx \)
これを「部分積分」といいます。特に、\(g(x) = x\) とすると、以下の式が成り立ちます。
\(
\displaystyle \int f(x) \, dx = x f(x) - \int x f'(x) \, dx
\)
簡単な例を示します。関数 \(\log_e x\) の積分を求めてみましょう。
\(\begin{eqnarray}
\displaystyle \int \log_e x &=& x \log_e x - \int x (\log_e x)' \, dx \\
&=& x \log_e x - \int x \dfrac{1}{x} \, dx \\
&=& x \log_e x - \int 1 \, dx \\
&=& x \log_e x - x
\end{eqnarray}\)
もう一つ、便利な公式を紹介しましょう。\(y = f(x)\) に対数微分法を適用すると、以下の公式を導くことができます。
\(\begin{array}{l}
\log_e y = \log_e f(x) \\
\dfrac{d}{dx} \log_e y = \dfrac{f'(x)}{f(x)} \\
\dfrac{d}{dx} \log_e f(x) = \dfrac{f'(x)}{f(x)}
\end{array}\)
両辺を積分すると以下の公式が成り立ちます。
\(
\displaystyle \int \dfrac{f'(x)}{f(x)} \,dx = \log_e |f(x)|
\)
ここで \(f(x) = x\) とすると、公式 \(\displaystyle \int \dfrac{1}{x} \,dx = \log_e |x|\) になります。
また、この公式は分数関数を積分するときにも役に立ちます。簡単な例を示しましょう。
\(\begin{eqnarray}
\displaystyle \int \dfrac{2x - 3}{x^2 - 3x + 2} \, dx
&=& \int \left(\dfrac{1}{x - 1} + \dfrac{1}{x - 2}\right) \,dx \\
&=& \displaystyle \int \dfrac{1}{x - 1} \,dx + \int \dfrac{1}{x - 2} \,dx \\
&=& \log_e |x - 1| + \log_e |x - 2|
\end{eqnarray}\)
分数関数には他にも積分公式がいくつかあります。
\(\begin{array}{lll}
& f(x) & F(x) \\
1. & \dfrac{1}{a^2 + x^2} & \dfrac{1}{a} \arctan {\dfrac{x}{a}} \quad (a \ne 0) \\
2. & \dfrac{1}{x^2 - a^2} & \dfrac{1}{2a} \log_e \left|\dfrac{x - a}{x + a}\right| \quad (a \ne 0) \\
3. & \dfrac{1}{\sqrt{a^2 - x^2}} & \arcsin {\dfrac{x}{a}} \quad (a \gt 0) \\
4. & \dfrac{1}{\sqrt{x^2 + a^2}} & \log_e \left|x + \sqrt{x^2 + a^2}\right| \quad (a \ne 0) \\
\end{array}\)
式 2 は部分分数に展開すると、簡単に求めることができます。他の式は次に説明する「置換積分」を使うと求めることができます。
式 2 の証明
部分分数に展開する
\(\begin{eqnarray} \dfrac{1}{x^2 - a^2} &=& \dfrac{1}{(x + a)(x - a)} \\ &=& \dfrac{1}{2a} \left(\dfrac{1}{x - a} - \dfrac{1}{x + a} \right) \\ \end{eqnarray}\)
積分する
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{x^2 - a^2} \,dx &=& \int \dfrac{1}{2a} \left(\dfrac{1}{x - a} - \dfrac{1}{x + a} \right) \,dx \\ &=& \dfrac{1}{2a} \left(\log_e |x - a| - \log_e |x + a| \right) \\ &=& \dfrac{1}{2a} \log_e \left|\dfrac{x - a}{x + a}\right| \end{eqnarray}\)
部分分数に展開する
\(\begin{eqnarray} \dfrac{1}{x^2 - a^2} &=& \dfrac{1}{(x + a)(x - a)} \\ &=& \dfrac{1}{2a} \left(\dfrac{1}{x - a} - \dfrac{1}{x + a} \right) \\ \end{eqnarray}\)
積分する
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{x^2 - a^2} \,dx &=& \int \dfrac{1}{2a} \left(\dfrac{1}{x - a} - \dfrac{1}{x + a} \right) \,dx \\ &=& \dfrac{1}{2a} \left(\log_e |x - a| - \log_e |x + a| \right) \\ &=& \dfrac{1}{2a} \log_e \left|\dfrac{x - a}{x + a}\right| \end{eqnarray}\)
●置換積分
関数 \(f(x)\) において、\(x = g(t)\) として変数 \(x\) を \(t\) に置換すると、以下の式が成り立ちます。
\(
\displaystyle \int f(x)\,dx = \int f(g(t)) g'(t)\,dt
\)
この方法を「置換積分」といいます。
公式の証明
\(y = \displaystyle \int f(x)\,dx, x = g(t)\) として、\(y\) を \(t\) で微分する
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \dfrac{dx}{dt} = f(x) \dfrac{d}{dt}g(t) = f(g(t)) g'(t) \)
両辺を t で積分すると
\( \displaystyle \int f(x)\,dx = \int f(g(t)) g'(t)\,dt \)
となり、公式を得る
\(y = \displaystyle \int f(x)\,dx, x = g(t)\) として、\(y\) を \(t\) で微分する
\( \dfrac{dy}{dt} = \dfrac{dy}{dx} \dfrac{dx}{dt} = f(x) \dfrac{d}{dt}g(t) = f(g(t)) g'(t) \)
両辺を t で積分すると
\( \displaystyle \int f(x)\,dx = \int f(g(t)) g'(t)\,dt \)
となり、公式を得る
簡単な例を示しましょう。
\(f(x) = (ax + b)^n, \ (n \ne -1)\) を積分する
\(t = ax + b\) とすると、\(x = \dfrac{t - b}{a}, \ \dfrac{dx}{dt} = \dfrac{1}{a}\) になる
よって、
\( \displaystyle \int (ax + b)^n \,dx = \int t^n \dfrac{1}{a} \,dt = \dfrac{t^{n+1}}{(n+1)a} = \dfrac{(ax + b)^{n+1}}{(n+1)a} \)
\(t = ax + b\) とすると、\(x = \dfrac{t - b}{a}, \ \dfrac{dx}{dt} = \dfrac{1}{a}\) になる
よって、
\( \displaystyle \int (ax + b)^n \,dx = \int t^n \dfrac{1}{a} \,dt = \dfrac{t^{n+1}}{(n+1)a} = \dfrac{(ax + b)^{n+1}}{(n+1)a} \)
なお、\(x = g(t)\) の微分を求めるところは、次のように行ってもかまいません。
\(t = ax + b\) とする
\(t\) を \(x\) で微分すると、\(\dfrac{dt}{dx} = a\) となる
ここで、便宜的に \(dx = \dfrac{1}{a} dt\) として置き換えてもよい
\(t\) を \(x\) で微分すると、\(\dfrac{dt}{dx} = a\) となる
ここで、便宜的に \(dx = \dfrac{1}{a} dt\) として置き換えてもよい
\(f(x) = \dfrac{1}{ax + b}\) を積分する
\(t = ax + b\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = a \quad \therefore \ dx = \dfrac{1}{a} dt\)
よって、
\( \displaystyle \int \dfrac{1}{ax + b} \,dx = \int \dfrac{1}{t} \dfrac{1}{a} \,dt = \dfrac{1}{a} \log_e |t| = \dfrac{1}{a} \log_e |ax + b| \)
\(t = ax + b\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = a \quad \therefore \ dx = \dfrac{1}{a} dt\)
よって、
\( \displaystyle \int \dfrac{1}{ax + b} \,dx = \int \dfrac{1}{t} \dfrac{1}{a} \,dt = \dfrac{1}{a} \log_e |t| = \dfrac{1}{a} \log_e |ax + b| \)
\(f(x) = \dfrac{x}{\sqrt {x^2 - 1}}\) を積分する
\(t = x^2 - 1\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = 2x \quad \therefore \ 2x \,{dx} = dt\)
よって、
\(\begin{eqnarray} \displaystyle \int \dfrac{x}{\sqrt {x^2 - 1}} &=& \dfrac{1}{2} \int \dfrac{1}{\sqrt {x^2 - 1}} 2x\,dx \\ &=& \dfrac{1}{2} \int t^{-\frac{1}{2}}\,dt = t^{\frac{1}{2}} = \sqrt {x^2 - 1} \end{eqnarray}\)
\(t = x^2 - 1\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = 2x \quad \therefore \ 2x \,{dx} = dt\)
よって、
\(\begin{eqnarray} \displaystyle \int \dfrac{x}{\sqrt {x^2 - 1}} &=& \dfrac{1}{2} \int \dfrac{1}{\sqrt {x^2 - 1}} 2x\,dx \\ &=& \dfrac{1}{2} \int t^{-\frac{1}{2}}\,dt = t^{\frac{1}{2}} = \sqrt {x^2 - 1} \end{eqnarray}\)
\(f(x) = \dfrac{1}{a^2 + x^2}\) を積分する
\(t = \dfrac{x}{a}\) とすると
\(\dfrac{dt}{dx} = \dfrac{1}{a} \quad \therefore \,{dx} = a dt\)
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{a^2 + x^2} \,dx &=& \int \dfrac{1}{a^2(1 + t^2)} a dt = \dfrac{1}{a} \int \dfrac{1}{1 + t^2} dt\\ &=& \dfrac{1}{a} \arctan t = \dfrac{1}{a} \arctan \dfrac{x}{a} \\ \end{eqnarray}\)
\(t = \dfrac{x}{a}\) とすると
\(\dfrac{dt}{dx} = \dfrac{1}{a} \quad \therefore \,{dx} = a dt\)
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{a^2 + x^2} \,dx &=& \int \dfrac{1}{a^2(1 + t^2)} a dt = \dfrac{1}{a} \int \dfrac{1}{1 + t^2} dt\\ &=& \dfrac{1}{a} \arctan t = \dfrac{1}{a} \arctan \dfrac{x}{a} \\ \end{eqnarray}\)
\(f(x) = \dfrac{1}{\sqrt{a^2 - x^2}} \)を積分する
\(t = \dfrac{x}{a}\) とすると
\(\dfrac{dt}{dx} = \dfrac{1}{a} \quad \therefore \,{dx} = a dt\)
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{\sqrt{a^2 - x^2}} \,dx &=& \int \dfrac{1}{\sqrt{a^2(1 - t^2)}} a dt = \int \dfrac{1}{1 - t^2} dt\\ &=& \arcsin t = \arcsin \dfrac{x}{a} \\ \end{eqnarray}\)
\(t = \dfrac{x}{a}\) とすると
\(\dfrac{dt}{dx} = \dfrac{1}{a} \quad \therefore \,{dx} = a dt\)
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{\sqrt{a^2 - x^2}} \,dx &=& \int \dfrac{1}{\sqrt{a^2(1 - t^2)}} a dt = \int \dfrac{1}{1 - t^2} dt\\ &=& \arcsin t = \arcsin \dfrac{x}{a} \\ \end{eqnarray}\)
\(f(x) = \dfrac{1}{\sqrt{x^2 + a^2}}\) を積分する
\(t = x + \sqrt {x^2 + a^2} \) とすると
\(\begin{eqnarray} \dfrac{dt}{dx} &=& 1 + \dfrac{2x}{2 \sqrt{x^2 + a^2}} = \dfrac{x + \sqrt{x^2 + a^2}}{\sqrt{x^2 + a^2}} \\ &=& \dfrac{t}{\sqrt{x^2 + a^2}} \end{eqnarray}\)
\( \therefore \, \dfrac{1}{t} dt = \dfrac{1}{\sqrt{x^2 + a^2}}\,dx \)
よって、
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{\sqrt{x^2 + a^2}} \,dx &=& \int \dfrac{1}{t} \, dt \\ &=& \log_e |t| = \log_e \left|x + \sqrt{x^2 + a^2}\right| \end{eqnarray}\)
\(t = x + \sqrt {x^2 + a^2} \) とすると
\(\begin{eqnarray} \dfrac{dt}{dx} &=& 1 + \dfrac{2x}{2 \sqrt{x^2 + a^2}} = \dfrac{x + \sqrt{x^2 + a^2}}{\sqrt{x^2 + a^2}} \\ &=& \dfrac{t}{\sqrt{x^2 + a^2}} \end{eqnarray}\)
\( \therefore \, \dfrac{1}{t} dt = \dfrac{1}{\sqrt{x^2 + a^2}}\,dx \)
よって、
\(\begin{eqnarray} \displaystyle \int \dfrac{1}{\sqrt{x^2 + a^2}} \,dx &=& \int \dfrac{1}{t} \, dt \\ &=& \log_e |t| = \log_e \left|x + \sqrt{x^2 + a^2}\right| \end{eqnarray}\)
●定積分
\(F(x) = \displaystyle \int f(x)\, dx\) のとき、以下の式を「定積分」といいます。
\(
\displaystyle \int_a^b f(x)\, dx = \left[F(x)\right]_a^b = F(b) - F(a)
\)
区間 \([a, b]\) で \(f(x) \geqq 0\) のとき、\(y = f(x)\) と \(x\) 軸に挟まれる部分の面積を\(S\) とすると、\(S = F(b) - F(a)\) となります。
証明の概略
関数 \(y = f(x)\) と \(x\) 軸に挟まれる図形において、区間 \([a, x]\) の部分の面積を \(S(x)\) とする
\(x\) を \(\varDelta x\) だけ変化させると、\(S(x)\) は \(S(x + \varDelta x) - S(x)\) だけ変化する
区間 \(\varDelta x\) の中で、\(f(x)\) の最小値と最大値 \(m, M\) が存在するので以下の式が成り立つ
\(\begin{array}{l} m \varDelta x \leqq S(x + \varDelta x) - S(x) \leqq M \varDelta x \\ m \leqq \dfrac{S(x + \varDelta x) - S(x)}{\varDelta x} \leqq M \end{array}\)
ここで、極限 \(\varDelta x \to 0\) を取ると、左右の式は \(f(x)\) に収束し、中の式は微分の定義なので \(S'(x)\) になる
よって、はさみ打ちの原理により \(S'(x) = f(x)\) となる
両辺を積分すると \(S(x) = F(x) + C\)
\(S(a) = 0\) なので、\(C = - F(a), \ S(x) = F(x) - F(a)\) となる
区間 \([a, b]\) の面積は
\(S(b) = F(b) - F(a) = \left[ F(x) \right]_a^b = \displaystyle \int_a^b f(x) \,dx\) となる
関数 \(y = f(x)\) と \(x\) 軸に挟まれる図形において、区間 \([a, x]\) の部分の面積を \(S(x)\) とする
\(x\) を \(\varDelta x\) だけ変化させると、\(S(x)\) は \(S(x + \varDelta x) - S(x)\) だけ変化する
区間 \(\varDelta x\) の中で、\(f(x)\) の最小値と最大値 \(m, M\) が存在するので以下の式が成り立つ
\(\begin{array}{l} m \varDelta x \leqq S(x + \varDelta x) - S(x) \leqq M \varDelta x \\ m \leqq \dfrac{S(x + \varDelta x) - S(x)}{\varDelta x} \leqq M \end{array}\)
ここで、極限 \(\varDelta x \to 0\) を取ると、左右の式は \(f(x)\) に収束し、中の式は微分の定義なので \(S'(x)\) になる
よって、はさみ打ちの原理により \(S'(x) = f(x)\) となる
両辺を積分すると \(S(x) = F(x) + C\)
\(S(a) = 0\) なので、\(C = - F(a), \ S(x) = F(x) - F(a)\) となる
区間 \([a, b]\) の面積は
\(S(b) = F(b) - F(a) = \left[ F(x) \right]_a^b = \displaystyle \int_a^b f(x) \,dx\) となる
これとは逆に、図形の面積から定積分を定義するやり方もあります。大学の数学では、そちらが主流だと思います。興味のある方は調べてみてください。
定積分の簡単な例を示しましょう。
\(
\displaystyle \int_1^2 (x^2 + 1) \,dx = \left[ \dfrac{x^3}{3} + x \right]_1^2 = \dfrac{8}{3} + 2 - \left(\dfrac{1}{3} + 1\right) = \dfrac{10}{3}
\)
\(
\displaystyle \int_0^1 \dfrac{4}{x^2 + 1} \,dx = 4 \left[ \arctan x \right]_0^1 = 4 \left(\dfrac{\pi}{4} - 0\right) = \pi
\)
\(
\displaystyle \int_0^{\pi} \sin \theta \,d\theta = \left[ - \cos \theta \right]_0^{pi} = - \cos \pi + \cos 0 = 1 + 1 = 2
\)
以下に定積分の基本的な公式を示します。
\(\begin{array}{l}
\displaystyle \int_a^a f(x) \, dx = 0 \\
\displaystyle \int_a^b f(x) \, dx = - \int_b^a f(x) \, dx \\
\displaystyle \int_a^b f(x) \, dx = \int_a^b f(t) \, dt \\
\displaystyle \int_a^b (k f(x) + l g(x)) \, dx = k \int_a^b f(x) \, dx + l \int_a^b g(x) \, dx \\
\displaystyle \int_a^b f(x) \, dx = \int_a^c f(x) \, dx + \int_c^b f(x) \, dx
\end{array}\)
(\(k, l\) は定数)
(\(k, l\) は定数)
定積分の置換積分は、次のように区間を変更する必要があります。
関数 \(f(x)\) において、\(x = g(t), \ a = g(\alpha), \ b = g(\beta)\) とすると
\( \displaystyle \int_a^b f(x)\,dx = \int_\alpha^\beta f(g(t)) g'(t)\,dt \)
証明
\(F(x)\) を \(f(x)\) の原始関数とする
不定積分の公式により \(F(g(t))\) は \(f(g(t)) g'(t)\) の原始関数になる
よって、
\(\begin{eqnarray} \displaystyle \int_\alpha^\beta f(g(t)) g'(t)\,dt &=& F(g(\beta)) - F(g(\alpha)) \\ &=& F(b) - F(a) \\ &=& \displaystyle \int_a^b f(x)\,dx \end{eqnarray}\)
\( \displaystyle \int_a^b f(x)\,dx = \int_\alpha^\beta f(g(t)) g'(t)\,dt \)
証明
\(F(x)\) を \(f(x)\) の原始関数とする
不定積分の公式により \(F(g(t))\) は \(f(g(t)) g'(t)\) の原始関数になる
よって、
\(\begin{eqnarray} \displaystyle \int_\alpha^\beta f(g(t)) g'(t)\,dt &=& F(g(\beta)) - F(g(\alpha)) \\ &=& F(b) - F(a) \\ &=& \displaystyle \int_a^b f(x)\,dx \end{eqnarray}\)
簡単な例を示しましょう。
\(\displaystyle \int_0^1 \dfrac{x}{\sqrt {1- x^2}} \,dx\) を積分する
\(t = 1 - x^2\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = -2x \quad \therefore \ -2x \,{dx} = dt\)
\(x = 0\) のとき \(t = 1\), \(x = 1\) のとき \(t = 0\)
よって、
\(\begin{eqnarray} \displaystyle \int_0^1 \dfrac{x}{\sqrt {1- x^2}} \,dx &=& -\dfrac{1}{2} \int_1^0 t^{-\frac{1}{2}} \,dt = \dfrac{1}{2} \int_0^1 t^{-\frac{1}{2}} \,dt \\ &=& \dfrac{1}{2} \left[ 2t^{\frac{1}{2}} \right]_0^1 = 1^{\frac{1}{2}} - 0^{\frac{1}{2}} = 1 \end{eqnarray}\)
\(t = 1 - x^2\) として \(t\) を \(x\) で微分すると
\(\dfrac{dt}{dx} = -2x \quad \therefore \ -2x \,{dx} = dt\)
\(x = 0\) のとき \(t = 1\), \(x = 1\) のとき \(t = 0\)
よって、
\(\begin{eqnarray} \displaystyle \int_0^1 \dfrac{x}{\sqrt {1- x^2}} \,dx &=& -\dfrac{1}{2} \int_1^0 t^{-\frac{1}{2}} \,dt = \dfrac{1}{2} \int_0^1 t^{-\frac{1}{2}} \,dt \\ &=& \dfrac{1}{2} \left[ 2t^{\frac{1}{2}} \right]_0^1 = 1^{\frac{1}{2}} - 0^{\frac{1}{2}} = 1 \end{eqnarray}\)
●2 つの曲線間の面積
区間 \([a, b]\) において、\(f(x) \geqq g(x)\) のとき、曲線 \(y = f(x), \ y = g(x)\) と垂線 \(x = a, x = b\) で囲まれた図形の面積 \(S\) は次の式で求めることができます。
\(
S = \displaystyle \int_a^b f(x) \,dx - \int_a^b g(x) \,dx = \int_a^b (f(x) - g(x)) \, dx
\)
もしも、\(x = a, b\) が 2 曲線の交点 \(f(a) = g(a), f(b) = g(b)\) ならば、2 曲線で囲まれた図形の面積を求めることになります。
簡単な例を示しましょう。
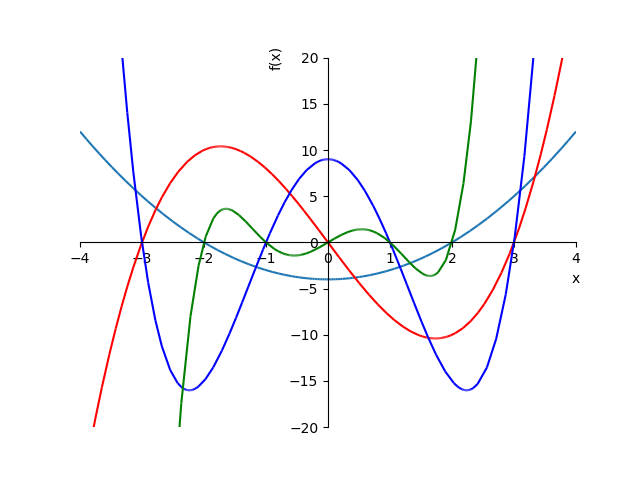
- \(f_1(x) = x^2 - 4\), (cyan)
- \(f_2(x) = x^3 - 9x\), (red)
- \(f_3(x) = x^4 - 10x^2 + 9\), (blue)
- \(f_4(x) = x^5 - 5x^3 + 4x\), (green)
\(\begin{array}{l}
\displaystyle \int_{-2}^2 -(x^2 - 4) \,dx = \left[-\dfrac{x^3}{3} + 4x\right]_{-2}^2 = \dfrac{32}{3} \\
\displaystyle \int_0^3 -(x^3 - 9x) \,dx = \left[-\dfrac{x^4}{4} + \dfrac{9x^2}{2}\right]_0^3 = \dfrac{81}{4} \\
\displaystyle \int_{-2}^0 (f_2(x) - f_1(x)) \,dx = \left[\dfrac{x^4}{4} - \dfrac{x^3}{3} - \dfrac{9x^2}{2} + 4x\right]_{-2}^0 = \dfrac{58}{3} \\
\displaystyle \int_{-1}^1 (f_3(x) - f_1(x)) \,dx = \left[\dfrac{x^5}{5} - \dfrac{11x^3}{3} + 13x\right]_{-1}^1 = \dfrac{286}{15} \\
\displaystyle \int_0^2 (f_4(x) - f_2(x)) \,dx = \left[\dfrac{x^6}{6} - \dfrac{3x^4}{2} + \dfrac{13x^2}{2}\right]_0^2 = \dfrac{38}{3}
\end{array}\)
SymPy での実行例を示します。
>>> import sympy as sy
>>> x = sy.var('x')
>>> f1 = x**2 - 4
>>> f2 = x**3 - 9*x
>>> f3 = x ** 4 - 10 * x ** 2 + 9
>>> f4 = x**5 - 5 * x**3 + 4*x
>>> sy.integrate(- f1, x)
-x**3/3 + 4*x
>>> sy.integrate(- f1, (x, -2, 2))
32/3
>>> sy.integrate(- f2, x)
-x**4/4 + 9*x**2/2
>>> sy.integrate(- f2, (x, 0, 3))
81/4
>>> sy.integrate(f2 - f1, x)
x**4/4 - x**3/3 - 9*x**2/2 + 4*x
>>> sy.integrate(f2 - f1, (x, -2, 0))
58/3
>>> sy.integrate(f3 - f1, x)
x**5/5 - 11*x**3/3 + 13*x
>>> sy.integrate(f3 - f1, (x, -1, 1))
286/15
>>> sy.integrate(f4 - f2, x)
x**6/6 - 3*x**4/2 + 13*x**2/2
>>> sy.integrate(f4 - f2, (x, 0, 2))
38/3
\(f_2(x), f_3(x)\) の交点を求めて、2 曲線間の図形の面積を求めます。
>>> sy.solveset(f2 - f3, x)
{-3, 3, 1/2 - sqrt(5)/2, 1/2 + sqrt(5)/2}
>>> sy.integrate(f2 - f3, (x, -3, (1 - math.sqrt(5))/2))
37.7610740869784
>>> sy.integrate(f3 - f2, (x, (1 - math.sqrt(5))/2, (1 + math.sqrt(5))/2))
15.8388148406235
>>> sy.integrate(f2 - f3, (x, (1 + math.sqrt(5))/2, 3))
6.87774075364509
●1/6 公式
ところで、放物線と直線で囲まれた図形の面積は、次の公式を使うと簡単に求めることができます。
\(
\displaystyle \int_{\alpha}^{\beta} (x - \alpha)(x - \beta) \,dx = - \dfrac{1}{6}(\beta -\alpha)^3
\)
\(\alpha, \ \beta\) は放物線と直線の交点 (x 座標) を表します。これを 1 / 6 公式といいます。
簡単な例を示しましょう。
\(y = 2x + 3, \ y = x^2\) で囲まれた図形の面積を求める
まず交点を求める
\(\begin{array}{l} x^2 = 2x + 3 \\ x^2 - 2x - 3 = 0 \\ (x - 3)(x + 1) = 0 \quad \therefore \ x = -1, 3 \end{array}\)
よって、 \( \displaystyle \int_{-1}^3 (2x + 3 - x^ 2) \,dx = -\int_{-1}^3 (x + 1)(x - 3) \,dx = \dfrac{32}{3} \)
まず交点を求める
\(\begin{array}{l} x^2 = 2x + 3 \\ x^2 - 2x - 3 = 0 \\ (x - 3)(x + 1) = 0 \quad \therefore \ x = -1, 3 \end{array}\)
よって、 \( \displaystyle \int_{-1}^3 (2x + 3 - x^ 2) \,dx = -\int_{-1}^3 (x + 1)(x - 3) \,dx = \dfrac{32}{3} \)
SymPy で検算してみましょう。
>>> sy.integrate(2*x + 3 - x**2, (x, -1, 3)) 32/3
公式を使って簡単に計算することができました。
1/6 公式の証明
\(\begin{eqnarray} \displaystyle \int_{\alpha}^{\beta} (x - \alpha)(x - \beta) \, dx &=& \int_{\alpha}^{\beta} (x - \alpha)((x - \alpha) + \alpha - \beta) \, dx \\ &=& \int_{\alpha}^{\beta} (x - \alpha)^2 + (\alpha - \beta)(x - \alpha) \, dx \\ &=& \left[\dfrac{(x - \alpha)^3}{3} + (\alpha - \beta)\dfrac{(x - \alpha)^2}{2} \right]_{\alpha}^{\beta} \\ &=& \dfrac{(\beta - \alpha)^3}{3} - \dfrac{(\beta - \alpha)^3}{2} = -\dfrac{(\beta - \alpha)^3}{6} \end{eqnarray}\)
\(\begin{eqnarray} \displaystyle \int_{\alpha}^{\beta} (x - \alpha)(x - \beta) \, dx &=& \int_{\alpha}^{\beta} (x - \alpha)((x - \alpha) + \alpha - \beta) \, dx \\ &=& \int_{\alpha}^{\beta} (x - \alpha)^2 + (\alpha - \beta)(x - \alpha) \, dx \\ &=& \left[\dfrac{(x - \alpha)^3}{3} + (\alpha - \beta)\dfrac{(x - \alpha)^2}{2} \right]_{\alpha}^{\beta} \\ &=& \dfrac{(\beta - \alpha)^3}{3} - \dfrac{(\beta - \alpha)^3}{2} = -\dfrac{(\beta - \alpha)^3}{6} \end{eqnarray}\)
式 \((x - \alpha)(x - \beta)\) を展開してから積分しても証明することができますが、式を \((x - \alpha)^n + \cdots \) の形に変形して積分すると、定積分の計算が簡単になります。\((x - \alpha)^n\) の積分は、\((ax + b)^n\) の積分公式から簡単に導くことができます。
\(
\displaystyle \int (x - \alpha)^n \,dx = \dfrac{(x - \alpha)^{n+1}}{n + 1} + C
\)