統計 [3]
●相関
今回は「相関 (correlation)」と「回帰 (regression)」について説明します。簡単にいうと、2 つの確率変数の間にある関連性のことを相関といい、一方が増加するにつれて他方も増加するまたは減少する傾向が見られるとき、相関関係 (または単に相関) があるといいます。
2 つの確率変数の間に相関が認められるとき、その関係を曲線や曲面で代表することを回帰といいます。とくに、相関が線形傾向の場合、その関係を一本の直線で示すことができます。これを「直線回帰」とか「線形回帰」といい、その直線を「回帰直線」といいます。回帰はデータの推計などで用いられる重要な手法の一つです。
●相関図
一方が増加するときに他方も増加傾向が見られる場合を「正の相関」があるといい、他方に減少傾向が見られる場合を「負の相関」があるといいます。また、相関関係が明瞭な場合を「強い相関」といい、不明瞭な場合を「弱い相関」といいます。文章で説明してもわかりにくいのて、図に示すことにしましょう。
たとえば、次のリストに示す対のデータ (x, y) が 30 個あります。
リスト : 対のデータ (1)
# 強い正の相関
data1 = [
(4.6, 5.5), (0.0, 1.7), (6.4, 7.2), (6.5, 8.3),
(4.4, 5.7), (1.1, 1.1), (2.8, 4.1), (5.1, 6.7),
(3.4, 5.0), (5.8, 6.6), (5.7, 6.3), (5.5, 5.6),
(7.9, 8.7), (3.0, 3.6), (6.8, 8.2), (6.2, 6.2),
(4.0, 5.0), (8.6, 9.5), (7.5, 8.9), (1.3, 2.6),
(6.3, 7.4), (3.1, 5.0), (6.1, 8.2), (5.3, 6.6),
(3.9, 5.1), (5.8, 7.0), (2.6, 3.5), (4.8, 6.3),
(2.2, 2.9), (5.3, 6.9)
]
これを平面上にプロットしたものを「相関図 (correlation diagram)」とか「散布図」といいます。下図を見てください。
横軸を x, 縦軸を y とすると、x が増加すると y も増加していることが一目でわかります。これが正の相関です。そして、点がある直線上に並んでいることもわかるでしょう。強い相関性を示しています。
ご参考までに、弱い相関と負の相関を示すデータと相関図を次に示します。
リスト : 対のデータ (2)
# 弱い正の相関
data2 = [
(4.6, 5.2), (0.0, 7.6), (6.4, 5.6), (6.5, 10.1),
(4.4, 8.0), (1.1, 0.0), (2.8, 6.5), (5.1, 10.2),
(3.4, 10.4), (5.8, 5.3), (5.7, 3.3), (5.5, 0.0),
(7.9, 7.0), (3.0, 0.5), (6.8, 10.4), (6.2, 0.0),
(4.0, 4.7), (8.6, 8.7), (7.5, 10.7), (1.3, 4.8),
(6.3, 8.1), (3.1, 10.7), (6.1, 17.9), (5.3, 9.0),
(3.9, 7.6), (5.8, 9.5), (2.6, 2.8), (4.8, 10.2),
(2.2, 0.0), (5.3, 10.8)
]
リスト : 対のデータ (3)
# 強い負の相関
data3 = [
(6.1, 3.7), (3.9, 7.5), (8.6, 1.7), (5.9, 3.9),
(3.5, 5.5), (7.0, 2.4), (0.9, 9.8), (0.0, 10.2),
(5.2, 4.2), (3.5, 6.5), (6.9, 3.2), (4.3, 5.9),
(5.0, 5.9), (7.4, 3.3), (3.1, 6.6), (4.0, 6.2),
(6.9, 2.9), (4.8, 5.0), (10.6, 0.0), (4.7, 4.3),
(2.9, 7.6), (7.2, 2.2), (3.6, 6.0), (5.5, 4.3),
(5.5, 4.5), (6.9, 3.2), (5.8, 3.6), (4.8, 4.6),
(7.3, 2.5), (4.7, 5.4)
]
リスト : 対のデータ (4)
# 弱い負の相関
data4 = [
(3.5, 10.2), (8.0, 0.0), (10.2, 3.0), (2.1, 10.8),
(2.8, 7.2), (3.7, 2.1), (5.1, 2.2), (7.5, 0.2),
(7.6, 4.6), (5.3, 0.3), (4.7, 6.0), (8.3, 5.4),
(4.8, 4.7), (6.6, 2.2), (2.4, 10.0), (4.4, 5.6),
(3.6, 9.3), (7.0, 3.0), (4.9, 3.1), (2.7, 4.4),
(9.2, 7.3), (3.7, 7.8), (0.8, 1.0), (4.8, 10.0),
(6.5, 1.1), (6.3, 0.9), (2.7, 4.9), (5.0, 3.9),
(3.4, 10.5), (6.6, 6.7),
]
●相関係数
統計学では、相関の強弱を表す統計量として「相関係数 (correlation coefficient)」を用います。相関係数の定義を次に示します。
x の分散 : \(\sigma_{x}^{2} = \dfrac{1}{N} \displaystyle \sum_{i=1}^N (x_{i} - x_{m})^{2}\)
y の分散 : \(\sigma_{y}^{2} = \dfrac{1}{N} \displaystyle \sum_{i=1}^N (y_{i} - y_{m})^{2}\)
x, y の共分散 : \(\sigma_{xy} = \dfrac{1}{N} \displaystyle \sum_{i=1}^N (x_{i} - x_{m})(y_{i} - y_{m})\)
x の平均 : \(x_{m} = \dfrac{1}{N} \displaystyle \sum_{i=1}^n x_{i} \)
y の平均 : \(y_{m} = \dfrac{1}{N} \displaystyle \sum_{i=1}^n y_{i} \)
まとめると
\( \rho_{xy} = \dfrac{\displaystyle \sum_{i=1}^N (x_{i} - x_{m})(y_{i} - y_{m})}{\sqrt{\displaystyle \sum_{i=1}^N(x_{i} - x_{m})^{2} \displaystyle \sum_{i=1}^N (y_{i} - y_{m})^{2}}} \)
\(σ_{xy}\) を「共分散 (covariance)」といいます。ちなみに、共分散も x と y の相関性を表しています。次の図を見てください。
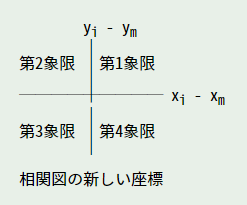
相関図で点 (\(x_{m}\) , \(y_{m}\)) が原点になるように座標を平行移動します。\((x - x_{m})(y - y_{m}) \gt 0\) を満たすデータ (x, y) は、第 1 象限もしくは第 3 象限にあります。したがって、第 1 象限もしくは第 3 象限にあるデータが多いほど、\(\sigma_{xy}\) は大きな正の値になり、正の相関を示すことになります。
逆に、第 2 象限と第 4 象限に多くのデータがあると、\(x - x_{m}\) と \(y - y_{m}\) の符号が逆になるので \(σ_{xy}\) は負の値になり、負の相関を示します。また、データが全ての象限に均等に散らばっているとすると、\(\sigma_{xy}\) は 0 に近い値になるはずです。この場合、相関性はほとんどありません。
ここで「シュワルツの不等式」を用いると、次の関係式が成り立ちます。
\( (a_{1}^{2} + a_{2}^{2} + \cdots + a_{n}^{2})(b_{1}^{2} + b_{2}^{2} + \cdots + b_{n}^{2}) \geqq (a_{1}b_{1} + a_{2}b_{2} + \cdots + a_{n}b_{n})^{2} \)
\( \displaystyle \sum_{i=1}^n a_{i}^{2} \sum_{i=1}^n b_{i}^{2} \geqq \left(\sum_{i=1}^n a_{i}b_{i}\right)^{2} \)
ここで \(a_{i} = x_{i} - x_{m}\), \(b_{i} = y_{i} - y_{m}\) とおくと
\( \displaystyle \sum_{i=1}^n (x_{i} - x_{m})^{2} \sum_{i=1}^n (y_{i} - y_{m})^{2} \geqq \left(\sum_{i=1}^n (x_{i} - x_{m})(y_{i} - y_{m})\right)^{2} \)
\( \dfrac {\sum_{i=1}^n (x_{i} - x_{m})(y_{i} - y_{m})}{\sqrt{\sum_{i=1}^n (x_{i} - x_{m})^{2} \sum_{i=1}^n (y_{i} - y_{m})^{2}}} \leqq 1 \)
よって \(\ -1 \leqq \rho_{xy} \leqq 1\) が成り立つ
相関係数 \(ρ_{xy}\) は 1 に近づくほど強い正の相関を表し、-1 に近づくほど強い負の相関を表します。正の相関も負の相関も見られないとき、x と y に相関はありません。この場合、相関係数は 0 になります。つまり、0 に近づくほど相関性はなくなるわけです。
data1, data2, data3, data4 の相関係数を求めると下表のようになります。
: 相関係数
------+----------
data1 : 0.968
data2 : 0.352
data3 : -0.969
data4 : -0.384
相関係数からも data1 と data3 は強い相関で、data2 と data4 は弱い相関であることが分かります。一般に、相関係数の解釈は次のようになります。
| 絶対値 | 解釈 |
|---|---|
| 0.7 ~ 1.0 | 強い相関がある |
| 0.4 ~ 0.7 | 中程度の相関がある |
| 0.2 ~ 0.4 | 弱い相関がある |
| 0.0 ~ 0.2 | ほとんど相関がない |
ここで、相関係数は 2 つの確率変数の間にある線形的な相関関係を表していることに注意してください。相関図で線形的な相関関係がある場合、データの近くを通る直線 (回帰直線) を引くことができます。
●回帰
2 つの確率変数の間に相関が認められるとき、その関係を曲線や曲面で代表することを「回帰 (regression)」といいます。相関に線形傾向が見られる場合、その関係を一本の直線で表すことができます。これを「直線回帰」とか「線形回帰」といい、その直線を「回帰直線」といいます。
回帰直線は次に示す式で求めることができます。
\(\begin{array}{l} a = \dfrac{\displaystyle \sum_{i=1}^n (x_{i} - x_{m})(y_{i} - y_{m})}{\displaystyle \sum_{i=1}^n (x_{i} - x_{m})^{2}} \\ b = y_{m} - ax_{m} \end{array}\)
ご参考までに、data1, data2, data3, data4 の回帰直線を下図に示します。
相関の強さは回帰直線のまわりにデータが密集している度合いによって表されます。回帰直線の傾き方と相関の強弱に関係はありません。回帰直線のまわりにデータが密集しているほど線形関係が強くなり、離れるほど線形関係が弱くなります。相関係数でいうと、±1 に近づくほどデータは回帰直線のまわりに密集し、ちょうど ±1 になると全てのデータが回帰直線上に並びます。
●時系列データ
それでは簡単な例題として、東京の年平均気温が今後どの程度上昇するか、回帰を用いて推定してみましょう。データは 気象庁 年ごとの値 (東京) の 1975 年から 2021 年までの年平均気温を用いました。
| 1975 | 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 |
|---|---|---|---|---|---|---|---|
| 15.6 | 15.0 | 15.8 | 16.1 | 16.9 | 15.4 | 15.0 | 16.0 |
| 1983 | 1984 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
| 15.7 | 14.9 | 15.7 | 15.2 | 16.3 | 15.4 | 16.4 | 17.0 |
| 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 |
| 16.4 | 16.0 | 15.5 | 15.9 | 16.3 | 15.8 | 16.7 | 16.7 |
| 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
| 17.0 | 16.9 | 16.5 | 16.7 | 16.0 | 17.3 | 16.2 | 16.4 |
| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 17.0 | 16.4 | 16.7 | 16.9 | 16.5 | 16.3 | 17.1 | 16.6 |
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
| 16.4 | 16.4 | 15.8 | 16.8 | 16.5 | 16.5 | 16.6 |
このように、一定の時間経過によって計測されたデータ列のことを「時系列 (time series)」といいます。横軸を年、縦軸を平均気温として相関係数と回帰直線を求めたところ、下図のようになりました。
相関係数は 0.557 で、中程度の正の相関がありました。回帰直線は y = 0.025 * (x - 1975) + 15.69 になりました。1975 年から 2006 年のデータを使うと、相関係数が 0.580 で、回帰直線が y = 0.041 * (x - 1975) + 15.49 になります。平均気温は上昇しているようですが、その伸びは鈍化しているのかもしれません。
なお、この結果は単純な線形回帰での推定にすぎず、実際の予測にはもっと複雑なモデルが使われていることでしょう。あくまでも回帰の例題ということで、結果については本気にしないようお願いいたします。
今回のデータを下記リストに示します。
リスト : 東京の年平均気温 (1975 年 - 2021 年)
data = [
(0, 15.6), (1, 15.0), (2, 15.8), (3, 16.1), (4, 16.9),
(5, 15.4), (6, 15.0), (7, 16.0), (8, 15.7), (9, 14.9),
(10, 15.7), (11, 15.2), (12, 16.3), (13, 15.4), (14, 16.4),
(15, 17.0), (16, 16.4), (17, 16.0), (18, 15.5), (19, 16.9),
(20, 16.3), (21, 15.8), (22, 16.7), (23, 16.7), (24, 17.0),
(25, 16.9), (26, 16.5), (27, 16.7), (28, 16.0), (29, 17.3),
(30, 16.2), (31, 16.4), (32, 17.0), (33, 16.4), (34, 16.7),
(35, 16.9), (36, 16.5), (37, 16.3), (38, 17.1), (39, 16.6),
(40, 16.4), (41, 16.4), (42, 15.8), (43, 16.8), (44, 16.5),
(45, 16.5), (46, 16.6),
]
●移動平均法
ところで、年平均気温は年によって変動が大きいので、データの傾向を把握するのはけっこう大変です。短期変動または偶然におこる変動などがある場合、それらの影響を取り除く方法を「平滑化 (smoothing)」といい、その一つに「移動平均法 (moving average method)」という方法があります。
移動平均法の原理は簡単で、連続する n 個のデータの平均値を計算していくだけです。たとえば n = 3 の場合、1975, 1976, 1977 年の気温を平均すると 15.47 度になります。そして、中央の 1976 年の平均気温を 15.47 度に設定します。次は、1976, 1977, 1978 年の平均値を求めて、その値を 1977 年の平均気温にするわけです。時系列のデータを \(x_{1}, x_{2}, \ldots, x_{n}\) とすると、移動平均法で求めた平均値は次のようになります。
2 番目の値 \(= (x_{1} + x_{2} + x_{3}) / 3\)
・・・
i 番目の値 \(= (x_{i-1} + x_{i} + x_{i+1}) / 3\)
・・・
n-1 番目の値 \(= (x_{n-2} + x_{n-1} + x_{n}) / 3\)
n 番目の値
移動平均の項数はいくつでもかまいません。適当な項数を選択してください。項数を多くすると、それだけスムーズになります。
それでは、3 項移動平均と 5 項移動平均の結果を下図に示します。
相関係数 0.722, 回帰直線 y = 0.0245x + 15.71
相関係数 0.771, 回帰直線 y = 0.0248x + 15.71
どちらの場合も強い正の相関を示しています。このように移動平均法を用いることにより、データ全体の傾向が簡単にわかるようになります。