サンプルプログラムの作成
それでは、もう少し実用的なサンプルプログラムを二つ作ってみましょう。一つはテキストウィジェットを使ってドキュメントを表示するプログラムで、もう一つはキャンバスウィジェットを使って結果をグラフで表示するプログラムです。
●POD Viewer
Perl には perldoc という POD (Plain Old Documentation) 形式で書かれたドキュメントを検索するためのツールが用意されています。Windows の場合、DOS プロンプトで perldoc Tk と入力すれば、Tk の説明が画面に表示されます。ここでは perldoc の GUI ラッパーを作成してみましょう。Perl/Tk を使えば、簡単に GUI ラッパーを作成できます。
●テキストウィジェット
テキストウィジェットは Text メソッドで生成します。エントリーウィジェットがラインエディタとするならば、テキストウィジェットはスクリーンエディタに相当し、柔軟で高度なテキスト編集を行うことができます。
テキストウィジェットには標準動作が用意されていて、それだけでテキスト編集が可能になっています。また、特定の位置をマークしたり、特定の文字列に識別子(タグ)をつけることができます。そして、タグごとにフォントや色などの表示属性やバインディングを設定することができます。この機能により、テキストウィジェットは単なるテキスト編集だけではなく、ある単語をクリックしたら別のテキストを表示するといったハイパーテキストを構成することができます。
このように、多くの機能をもつテキストウィジェットですが、テキストを表示するだけならば簡単に使うことができます。
●ウィジェットの設定
検索するキーワードはエントリーウィジェットで入力します。perldoc には、関数の検索を行う -f オプションと、FAQ の検索を行う -q オプションがありますが、これらの指定はラジオボタンで行います。あとは perldoc を呼び出して、その出力をパイプで受け取り、それをテキストウィジェットに表示させればよいわけです。プログラムをリスト 8 に示します。
リスト 8 : Perl Doc Viewer
#
# list8.pl : Perl Doc Viewer
#
# Copyright (C) 2002 Makoto Hiroi
#
use Tk;
# グローバル変数
$opt = ' ';
$buffer = '';
# ドキュメントの表示
sub display {
# 前のドキュメントを消去
$t0->configure( -state => 'normal' );
$t0->delete( '1.0', 'end' );
# perldoc の実行
open IN, "perldoc $opt $buffer |" or die "Can't exec perldoc\n";
while( <IN> ){
$t0->insert( 'end', $_ );
}
close( IN );
$t0->configure( -state => 'disable' );
$t0->focusForce();
}
# ***** 画面の設定 *****
# メインウィンドウ
$top = MainWindow->new();
# フレーム
$f0 = $top->Frame();
$f1 = $top->Frame();
# フレーム $f0 内の配置
$l0 = $f0->Label( -text => 'Key word : ' )->pack(-side => 'left');
$e0 = $f0->Entry( -textvariable => \$buffer )->pack(-side => 'left');
$e0->bind("<Return>", \&display );
$f0->pack( -anchor => 'w' );
# フレーム $f1 内の配置
$r0 = $f1->Radiobutton( -text => 'Page, Module, Program',
-variable => \$opt, -value => ' ')->pack( -side => 'left' );
$r1 = $f1->Radiobutton( -text => 'Perl Function',
-variable => \$opt, -value => '-f')->pack( -side => 'left' );
$r2 = $f1->Radiobutton( -text => 'Perl FAQ',
-variable => \$opt, -value => '-q')->pack( -side => 'left' );
$f1->pack( -anchor => 'w' );
# テキストウィジェット
$t0 = $top->Scrolled( 'Text', -scrollbars => 'se', -wrap => 'none' )
->pack(-expand => 1, -fill => 'both');
$e0->focus;
MainLoop();
各ウィジェットはフレームウィジェット上に配置します。1 番目のフレームには、ラベルウィジェットとエントリーウィジェットを横に並べて配置します。このため、pack の -side オプションには left を指定します。
キーワードの入力が完了したらボタンを押してもらってもよいのですが、ここはマウスよりもキーボードで操作したほうがいいでしょう。リターンキーの入力で perldoc を起動します。このため、エントリーウィジェットには次のようにバインディングを設定します。
$e0->bind( "<Return>", \&display );
エントリーウィジェットのオブジェクトは変数 $e0 に格納されています。これでエントリーウィジェットでリターンキーを入力すると、関数 display が実行されます。
2 番目のフレームには、オプションを設定するラジオボタンを横に並べて配置します。最後に、テキストウィジェットを生成します。二つのフレームとテキストウィジェットは縦に並べて配置します。フレーム内のウィジェットは左側に寄せて配置したいので、-anchor オプションを使っています。何も指定しないとウィドウの中央に配置されます。
●Scrolled メソッド
テキストウィジェットにはスクロールバーを取り付けます。Tk に用意されているスクロールバーウィジェットは、単独で使われることはほとんどなく、関連付けられたウィジェットを制御するために用いられます。このため、Perl/Tk には Scrolled という便利なメソッドが用意されていて、指定したウィジェットにスクロールバーを簡単に取り付けることができます。Scrolled メソッドは次の形式で呼び出します。
$widget = $parent->Scrolled( widgetClass, -scrollbars => value );
テキストウィジェットにスクロールバーをつける場合、widgetClass には Text を指定します。リストボックスであれば Listbox を指定します。オプション -scrollbars には、スクロールバーを付ける方向を指定します。方向は n (上), s (下), e (右), w (左) で、se と指定すれば下と右の 2 か所にスクロールバーを設置することができます。Scrolled メソッドの返り値は、widgetClass で指定したウィジェットのオブジェクトです。
●テキストの表示
テキストの表示は関数 display で行います。最初に、表示していたテキストを削除します。-state はウィジェットの状態を表すオプションです。値は normal, active, disabled の 3 種類があります。ウィジェットの -state に disabled を指定すると、そのウィジェットを無効にすることができます。テキストウィジェットの場合、disabled を指定するとテキストの変更が禁止されます。
最初に -state を normal に戻してからテキストを delete メソッドで削除します。1.0 は 1 行目の 0 文字、つまりテキストの先頭を表しています。end はテキストの末尾を表します。位置の指定はいくつか方法があるので、文献やマニュアルを参照してください。
次に、open で perldoc を起動してパイプからデータを読み込みます。テキストの挿入は insert メソッドで行います。パイプから 1 行ずつ読み込み、テキストの最後尾へ追加します。あとは close でパイプを閉じて、configure で -state を disabled に変更します。これでテキストを書き換えることはできません。最後に、focusForce メソッドでフォーカスをテキストウィジェットに設定します。
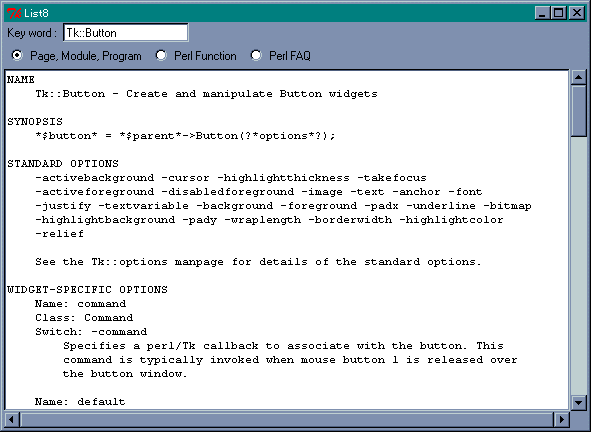
これでプログラムは完成です。ボタンの説明を表示した画面を図 19 に示します。サンプルプログラムは perldoc を使いましたが、ほかの CUI コマンドでも出力を表示することは簡単です。
図 19 : リスト 8 の画面
巡回セールスマン問題
次は、キャンバスウィジェットを使ったサンプルを作ります。例題として「巡回セールスマン問題」を取り上げます。この問題は有名なのでご存知の方も多いでしょう。セールスマンは各都市を 1 回ずつもれなく訪問して帰ってこなくてはいけません。このとき、一番短い巡路(すべての都市を含む単純な閉路)を見つけるのが巡回セールスマン問題 (TSP) の目的です。
TSP は都市の個数が増えると、厳密解を求めるのが非常に困難になります。このため、近似解を求めるアルゴリズムがいろいろ考案されています。ここでは、既存のプログラムを呼び出すことで近似解を求めることにし、座標の設定と結果の表示を GUI で行うことにします。
GUI 表示を行うプログラムを リスト 9 に、近似解を求めるプログラムを リスト 10 に示します。
●キャンバスウィジェット
キャンバスウィジェットは、矩形、直線、楕円などの図形のほかに、イメージ、文字列、任意のウィジェットを表示することができます。キャンバスウィジェットは Canvas メソッドで生成し、図形を描くには create メソッドを使います。
$canvas->create(type, x, y, ..., option => value, ...);
図形の種別 (type) を表 6 に示します。create メソッドは、図形を表す番号 (ID) を返します。この ID を使って図形を操作します。また、図形には -tags オプションでタグをつけることができ、ID のかわりにタグを使って図形を操作できます。図形を操作するときによく使うメソッドを表 7 に示します。
| 図形名 | 説明 |
|---|---|
| line | 直線(折れ線) |
| oval | 円、楕円 |
| arc | 円弧(楕円の円周の一部) |
| rectangle | 矩形 |
| polygon | 多角形 |
| image | イメージ |
| bitmap | ビットマップ |
| text | 文字列 |
| window | 任意のウィジェット |
| メソッド名 | 説明 |
|---|---|
| type(IDorTAG) | 図形の種別を返す |
| bbox(IDorTAG, ...) | 指定した図形を囲む領域(矩形)をリストにして返す |
| coords(IDorTAG, x0, y0, ...) | 図形の座標の設定や問い合わせ |
| delete(IDorTAG, ...) | 図形の削除 |
| move(IDorTAG, dx, dt) | 図形の移動 |
| lower(IDorTAG1, IDorTAG2) | 重なり順を低くする |
| raise(IDorTAG1, IDorTAG2) | 重なり順を高くする |
それから、図形にはウィジェットと同様に bind メソッドでバインディングを設定することができます。
$canvas->bind( IDorTag, eventsequence, callback );
変数 $canvas はキャンバスウィジェットのオブジェクトです。第 1 引き数に図形を指定します。図形の指定は ID とタグのどちらでもかまいません。図形ごとにバインディングを設定できるので、ドラッグで図形を移動させるといった複雑な操作も簡単に行えます。
●図形の生成
このプログラムで必要になる図形は、背景(白)、グラフを表す線、都市を表すポイント、ポイントを結ぶラインの 4 種類があります。都市の個数は最大 128 とし、必要な図形はあらかじめ生成しておきます。このとき、図形にはタグを設定します。背景と方眼紙を表す線には back、都市を表すポイントには point、ポイントを結ぶラインには line をつけます。ポイントは小さな正方形で表します。
ウィジェットには、ウィンドウシステムのように重なり順があります。Tk の場合は、後から作成したウィジェットが上になります。キャンバスウィジェットで作成する図形も同じで、後から作成した図形が上になります。ウィジェットや図形の重なり順は、メソッド raise と lower で変更することができます。不要な図形は lower で背景の下に隠しておき、必要になったら raise で表に出すことにします。
●座標の設定
ポイントの位置はマウスの左ボタンで設定します。タグ back の図形上で左ボタンを押したら、そこにポイントを設定します。ポイントを設定する関数を set_point とすると、バインディングの設定は次のようになります。
$canvas->bind( 'back', "<Button-1>" => [\&set_point, Ev('x'), Ev('y')] );
これでタグ back を持つ図形すべてにバインディングを設定することができます。マウスの座標は関数 Ev( 'x' ) と Ev( 'y' ) で求めます。set_point では未使用のポイントを取り出し、coords メソッドで (x, y) へ移動して raise メソッドで表に出します。
ポイントの位置を変更する場合はポイントをドラッグします。ポイントの移動を行う関数を move_point とすると、バインディングの設定は次のようになります。
$canvas->bind( 'point', "<B1-Motion>" => [\&move_point, Ev('x'), Ev('y')]);
ドラッグを表すイベントは <B1-Motion> です。ただし、このままでは関数 move_point で操作対象となるポイントがわかりません。この場合は特別なタグ current を使います。
current は Tk が設定するタグで、マウスカーソルがある図形上にくると、その図形に current を設定します。そして、その図形からマウスカーソルが出ると current を削除します。つまり、マウスカーソルが指している図形は current で特定することができるのです。move_point では coords に current を指定して、ポイントをドラッグで移動します。
ポイントを削除する場合はポイント上で右ボタンを押します。ポイントを削除する関数を clear_point とするとバインディングの設定は次のようになります。
$canvas->bind('point', "<Button-3>" => \&clear_point);
Windows の場合、右ボタンを押すイベントは <Button-3> になります。clear_point では、find メソッドを使って curren タグを持つポイントの ID を求め、それを未使用状態に戻します。
これらのバインディングを設定することで、ポイントの位置をマウスで設定することができます。
●メニューの設定
座標設定以外の操作はメニューで行います。Tk はメニューのためのウィジェットがいくつか用意されていますが、ここではメニューバーを使います。メニューは Menu メソッドで生成します。メニューバーの場合は -type オプションで menubar を指定します。生成したメニューバーはメインウィンドウの -menu オプションで配置します。設定は次のように行います。
$top = MainWindow->new(); $m = $top->Menu( -type => 'menubar' ); $top->configure( -menu => $m );
これでメインウィンドウにメニューバーが設定されます。そして、このメニューバーに具体的なメニューを追加します。メニューを設定するおもなメソッドを表 8 に、おもなオプションを表 9 に示します。
| メソッド名 | 説明 |
|---|---|
| cascade | 複数のメニューを表示する |
| checkbutton | チェックボタンを表示 |
| command | -command オプションで指定した関数を実行 |
| radiobutton | ラジオボタンを表示 |
| separator | 区切りを表示する |
| オプション名 | 説明 |
|---|---|
| -command | 項目の選択時に実行されるコールバック関数 |
| -label | メニューに表示される文字列 |
| -offvalue | チェックボタンでオフになったときの値 |
| -onvalue | チェックボタンでオンになったときの値 |
| -tearoff | メニューをウィンドウから切り離すか否か |
| -underline | ラベルの文字列に下線を引く |
| -value | ラジオボタンの項目を選択したときの値 |
| -variable | ラジオボタンの値を格納する変数 |
メニューは File, Clear, Solve の三つを用意しました。File はポイントの座標をランダムで設定するための項目と、プログラムを終了するための項目を設定します。経路の消去は clear で行います。ここで Line を選択すると経路だけ消去され、All を選択すると経路とポイントの両方が消去されます。
ポイントの座標を設定したら、Solve を選択して近似解を求めます。近似解はプログラム tsp (リスト 10) で求めます。座標はテンポラリファイルに格納して、それを tsp へ渡します。tsp は訪問するポイントの座標を順番に出力するので、それをパイプ経由で受け取り配列 @xpoint と @ypoint に格納します。そして、draw_line を呼び出して画面に経路を表示します。
draw_line では、@xpoint と @ypoint から座標を取り出し、あらかじめ生成しておいたラインを使ってポイントの間を直線で結びます。この処理は、coords メソッドでラインをその座標へ移動し、raise メソッドで表に出すだけです。これで経路を表示することができます。
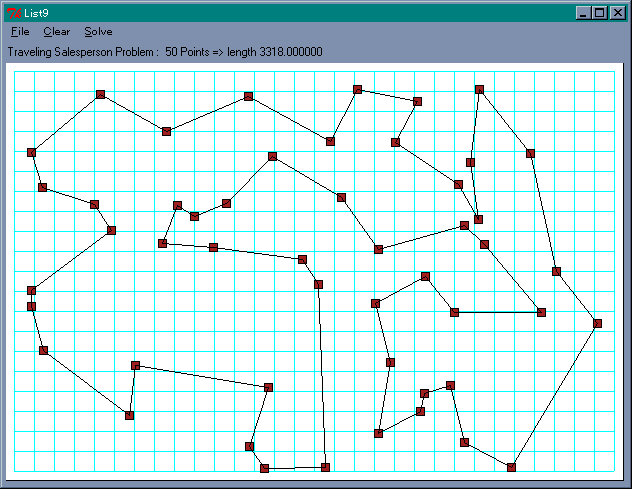
座標入力の画面を図 20 に、経路の表示を図 21 に示します。
図 20 : 座標入力の画面
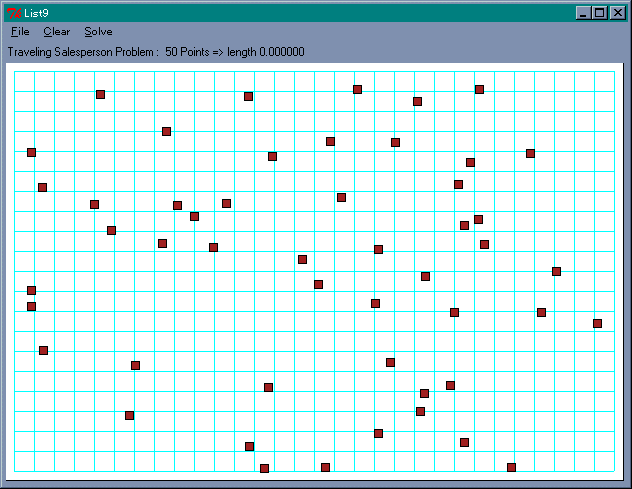
図 21 : 経路表示の画面
おわりに
駆け足で Perl/Tk の機能とプログラミングの方法を説明しました。このほかにも、Perl/Tk にはたくさんのウィジェットや機能が用意されています。限られた誌面でそのすべてを紹介することは不可能ですが、必要なウィジェットを配置してバインディングを設定するだけで GUI アプリケーションを作成できるという Perl/Tk の特徴は説明できたのではないかと思っています。
とくに、ウィジェットのオプションや対応できるイベントはとても多いので、マニュアルや文献などを参照してください。また、Tcl/Tk のウィジェットで利用できるオプションは、ほとんどの場合 Perl/Tk でも利用できるので、Tcl/Tk のマニュアルも参考になるでしょう。
簡単に GUI アプリケーションを作成できるところが Perl/Tk の長所ですが、その点では Tcl/Tk も負けてはいません。むしろ Tcl/Tk の方が簡単かもしれません。ですが、Perl/Tk で GUI アプリケーションを作成する場合、Perl の優れたライブラリ資産をそのまま利用できることは、とても大きなメリットになるはずです。「簡単なことは簡単に。難しいことは可能に」という Perl のポリシーは、そのまま Perl/Tk にもあてはまるのです。
Perl はもっとも普及しているスクリプト言語の一つです。その Perl で簡単に GUI アプリケーションを作成できる Perl/Tk は、多くの方にとって有用な GUI 開発ツールになるでしょう。
最後に、本稿が GUI に関心を持たれている読者の参考になれば幸いです。
参考文献
- Larry Wall, Tom Christiansen, Randal L. Schwartz, 『プログラミングPerl改訂版』 オライリー・ジャパン, 1997
- Sriram Srinivasan, 『実用Perlプログラミング』 オライリー・ジャパン, 1998
- Stepben Lidie, 『Perl/Tk ディスクトップリファレンス』 オライリー・ジャパン, 1999
●リスト 9 : 巡回セールスマン問題の経路を表示
#
# list9.pl : 巡回セールスマン問題の経路を表示
#
# Copyright (C) 2001 Makoto Hiroi
#
use Tk;
# グローバル変数
@free_point = ();
@used_point = ();
@free_line = ();
@used_line = ();
@xpoint = ();
@ypoint = ();
# 状態
$INIT_MODE = 0;
$INPUT_MODE = 1;
$SOLVE_MODE = 2;
$state = $INIT_MODE;
$message = "Traveling Salesperson Problem";
# メッセージの表示
sub display_message {
my $len = shift;
my $num = @used_point;
$message = sprintf("Traveling Salesperson Problem : %3d Points => length %f", $num, $len );
}
# point の移動
sub move_point {
my ($obj, $x, $y) = @_;
return if $state != $INPUT_MODE;
$canvas->coords( 'current', $x - 4, $y - 4, $x + 4, $y + 4 );
}
# line を描画
sub draw_line {
my $x0 = $xpoint[0];
my $y0 = $ypoint[0];
my $i;
push( @xpoint, $x0 );
push( @ypoint, $y0 );
for( $i = 1; $i < @xpoint; $i++ ){
my $x1 = $xpoint[$i];
my $y1 = $ypoint[$i];
my $id = pop( @free_line );
push( @used_line, $id );
$canvas->coords( $id, $x0, $y0, $x1, $y1 );
$canvas->raise( $id );
$x0 = $x1;
$y0 = $y1;
}
}
# 解を求める
sub solve {
my $filename = "tmp$$.dat";
my $len;
return if $state == $SOLVE_MODE or @used_point == 0;
# 初期化
@xpoint = ();
@ypoint = ();
open( OUT, ">$filename" );
foreach $id ( @used_point ){
# coords で返ってくるのは左上隅の座標
my ($x, $y) = $canvas->coords( $id );
$x += 4;
$y += 4;
print OUT "$x $y\n";
}
close( OUT );
# プログラムを起動
open( IN, "tsp < $filename |" );
while( <IN> ){
if( /([0-9]+) ([0-9]+)/ ){
push( @xpoint, $1 );
push( @ypoint, $2 );
} elsif( /length (.*)/ ){
$len = $1;
}
}
close( IN );
unlink( $filename );
# line を描画
&draw_line;
$state = $SOLVE_MODE;
&display_message( $len );
}
# point の設定
sub set_point {
my ($obj, $x, $y) = @_;
return if $state == $SOLVE_MODE;
my $id = pop( @free_point );
if( $id ){
push( @used_point, $id );
$canvas->coords( $id, $x - 4, $y - 4, $x + 4, $y + 4 );
$canvas->raise( $id );
}
$state = $INPUT_MODE;
&display_message( 0 );
}
# point のクリア
sub clear_point {
return if $state == $SOLVE_MODE;
my $id = $canvas->find( withtag => 'current' );
if( $id ){
my $i;
for( $i = 0; $i < @used_point; $i++ ){
last if $id == $used_point[$i];
}
splice( @used_point, $i, 1 );
$state = $INIT_MODE if @used_point == 0;
push( @free_point, $id );
$canvas->lower( $id );
}
&display_message( 0 );
}
# 乱数によるセット
sub random_set {
my $n = shift;
my ($x, $y);
return if $state != $INIT_MODE;
while( $n-- > 0 ){
$x = int( rand 600 ) + 10;
$y = int( rand 400 ) + 10;
set_point( $canvas, $x, $y );
}
&display_message( 0 );
}
# クリア
sub line_clear {
my $id;
while( $id = pop( @used_line ) ){
push( @free_line, $id );
$canvas->lower( $id );
}
$state = $INPUT_MODE;
&display_message( 0 );
}
sub all_clear {
my $id;
while( $id = pop( @used_point ) ){
push( @free_point, $id );
$canvas->lower( $id );
}
&line_clear;
$state = $INIT_MODE;
&display_message( 0 );
}
# ***** 画面の設定 ******
$top = MainWindow->new();
# メニューの設定
$m = $top->Menu( -type => 'menubar' );
$top->configure( -menu => $m );
$m1 = $m->cascade(-label => 'File', -underline => 0, -tearoff => 0);
$m2 = $m->cascade(-label => 'Clear', -underline => 0, -tearoff => 0);
$m3 = $m->command(-label => 'Solve', -underline => 0, -command => \&solve);
$m1->command(-label => 'Random 25 points', -command => [\&random_set, 25]);
$m1->command(-label => 'Random 50 points', -command => [\&random_set, 50]);
$m1->command(-label => 'Random 75 points', -command => [\&random_set, 75]);
$m1->command(-label => 'Random 100 points', -command => [\&random_set, 100]);
$m1->separator;
$m1->command(-label => 'Exit', -underline => 0, -command => \&exit );
$m2->command(-label => 'Line', -underline => 0, -command => \&line_clear);
$m2->command(-label => 'All', -underline => 0, -command => \&all_clear);
$label = $top->Label( -textvariable => \$message )->pack( -anchor => 'w' );
$canvas = $top->Canvas( -width => 620, -height => 420 )->pack();
$back = $canvas->create('rectangle', 1, 1, 619, 419, -fill => 'white', -tags => 'back' );
# グラフ
for( $x = 10; $x <= 610 ; $x += 20 ){
$canvas->create( 'line', $x, 10, $x, 410, -fill => 'cyan', -tags => 'back' );
}
for( $y = 10; $y <= 410; $y += 20 ){
$canvas->create( 'line', 10, $y, 610, $y, -fill => 'cyan', -tags => 'back' );
}
$canvas->bind( 'back', "<Button-1>" => [\&set_point, Ev('x'), Ev('y')] );
# point, line の作成
for( $i = 0; $i < 128; $i++ ){
my $id = $canvas->create( 'rectangle', 10, 10, 20, 20,
-fill => 'brown', -tags => 'point' );
push( @free_point, $id );
$canvas->lower($id);
$id = $canvas->create( 'line', 10, 10, 18, 18, -tags => 'line' );
push( @free_line, $id );
$canvas->lower($id);
}
# point 移動のためのバインド
$canvas->bind( 'point', "<B1-Motion>" => [\&move_point, Ev('x'), Ev('y')]);
# point クリアのためのバインド
$canvas->bind( 'point', "<Button-3>" => \&clear_point);
# 乱数の初期化
srand();
MainLoop();
●リスト 10 : 巡回セールスマン問題
/*
* tsp.c : 巡回セールスマン問題
* 分割統治法+深さ優先探索による解法
*
* Copyright (C) 2002 Makoto Hiroi
*
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <float.h>
#define SIZE 128 /* 点の最大値 */
#define TRUE 1
#define FALSE 0
#define TATE 0 /* 分割の方向 */
#define YOKO 1
#define MAX_SIZE 10
/* 双方向リストメモリ管理テーブル */
#define NODE_TABLE_SIZE 256
#define NODE_ALLOC_SIZE 1024
/* 要素を交換するマクロ */
#define SWAP( i, j ) { \
POINT tmp = point_table[(i)]; \
point_table[(i)] = point_table[(j)]; \
point_table[(j)] = tmp; \
}
/* 差を求める */
#define DIFFER( i, j, k ) distance( (i)->data, (j)->data ) \
+ distance( (i)->data, (k)->data ) - distance( (j)->data, (k)->data )
/* 点を表す構造体 */
typedef struct {
short x;
short y;
} POINT;
/* 双方向リストの定義 */
typedef struct _node {
POINT data;
struct _node *prev;
struct _node *next;
} NODE;
/* 点を格納する外部変数 */
POINT point_table[SIZE + 10];
NODE *node_table[NODE_TABLE_SIZE];
NODE *node_top;
int table_size = 0;
int node_count = 0;
/* メモリ管理 */
NODE *get_node( void )
{
NODE *p;
if( node_count >= NODE_ALLOC_SIZE ) node_count = 0;
if( !node_count ){
node_top = malloc( sizeof( NODE ) * NODE_ALLOC_SIZE );
if( node_top == NULL || table_size >= NODE_TABLE_SIZE){
fprintf( stderr, "メモリが足りません\n");
exit( 1 );
}
node_table[table_size++] = node_top;
}
p = node_top + node_count++;
p->prev = p->next = p; /* 自分自身に初期化しておく */
return p;
}
/* メモリ解放 */
void node_free( void )
{
int i;
for( i = 0; i < table_size ; i++ ) free( node_table[i] );
}
char visited[MAX_SIZE]; /* 通過した頂点に印をつける */
char path[MAX_SIZE]; /* 経路 */
char min_path[MAX_SIZE]; /* 最短経路 */
double min_length; /* 長さ */
/* 各点の距離を格納 */
double distance_table[MAX_SIZE][MAX_SIZE];
/* 距離を計算してテーブルにセットする */
void set_distance_table( int start, int size )
{
int i, j;
for( i = 0; i < size; i++ ){
for( j = 0; j < size; j++ ){
int dx = point_table[start + i].x - point_table[start + j].x;
int dy = point_table[start + i].y - point_table[start + j].y;
distance_table[i][j] = sqrt( dx * dx + dy * dy );
}
}
}
/* 探索する(深さ優先探索) */
void search( int num, int size, double len )
{
double now_len;
if( num == size ){
/* 始点と終点を結ぶ */
now_len = len + distance_table[0][ path[num - 1] ];
if( now_len < min_length ){
/* 最短経路を更新 */
memcpy( min_path, path, size );
min_length = now_len;
}
} else {
int i;
for( i = 1; i < size; i++ ){
if( !visited[i] ){
now_len = len + distance_table[i][ path[num - 1] ];
if( now_len < min_length ){
visited[i] = TRUE;
path[num] = i;
search( num + 1, size, now_len );
visited[i] = FALSE;
}
}
}
}
}
/* 自明な場合に頂点を双方向リストにまとめる */
NODE *make_node( int s, int n )
{
NODE *p;
int i;
/* テーブル初期化 */
set_distance_table( s, n );
for( i = 0; i < n; i++ ) visited[i] = FALSE;
/* 始点 0 をセットする */
visited[0] = TRUE;
path[0] = 0;
min_length = DBL_MAX; /* 長さの初期化 */
search( 1, n, 0 );
p = get_node();
p->data = point_table[s];
for( i = 1; i < n; i++ ){
NODE *q = get_node();
q->data = point_table[s + min_path[i] ];
q->next = p->next;
q->prev = p;
p->next->prev = q;
p->next = q;
}
return p;
}
/* 距離を計算する */
double distance( POINT p1, POINT p2 )
{
int dx = p1.x - p2.x;
int dy = p1.y - p2.y;
return sqrt( dx * dx + dy * dy );
}
/* 標準入力より点データを読み込む */
int read_point_data( void )
{
char buffer[256];
int i, x, y;
for( i = 0; i < SIZE; i++ ){
if( fgets( buffer, 256, stdin ) == NULL ) break;
sscanf( buffer, "%d %d", &x, &y );
point_table[i].x = x;
point_table[i].y = y;
}
return i;
}
/* 分割する方向を求める */
int divide_direction( int start, int n )
{
int i, max_x, min_x, max_y, min_y;
max_x = min_x = point_table[start].x;
max_y = min_y = point_table[start].y;
for( i = start + (n & 0x01); i < (start + n); i += 2 ){
int x1 = point_table[i].x;
int y1 = point_table[i].y;
int x2 = point_table[i + 1].x;
int y2 = point_table[i + 1].y;
if( x1 < x2 ){
if( min_x > x1 ) min_x = x1;
if( max_x < x2 ) max_x = x2;
} else {
if( min_x > x2 ) min_x = x2;
if( max_x < x1 ) max_x = x1;
}
if( y1 < y2 ){
if( min_y > y1 ) min_y = y1;
if( max_y < y2 ) max_y = y2;
} else {
if( min_y > y2 ) min_y = y2;
if( max_y < y1 ) max_y = y1;
}
}
return (((max_x - min_x) > (max_y - min_y)) ? TATE : YOKO);
}
/* 比較関数 */
int comp_x( POINT i, POINT j )
{
int r = i.x - j.x;
if( !r ) r = i.y - j.y;
return r;
}
int comp_y( POINT i, POINT j )
{
int r = i.y - j.y;
if( !r ) r = i.x - j.x;
return r;
}
/* 真ん中の要素を基準に2分割する */
int divide( int start, int num, int (*comp)( POINT, POINT ) )
{
int m = start + (num / 2);
int end = start + num - 1;
while( start < end ){
POINT p = point_table[m];
int i = start;
int j = end;
for(;;){
while( (*comp)( p, point_table[i] ) > 0 ) i++;
while( (*comp)( p, point_table[j] ) < 0 ) j--;
if( i > j ) break;
SWAP( i, j );
i++, j--;
}
if( j < m ) start = i;
if( m < i ) end = j;
}
return m;
}
/* 双方向リスト(経路)を表示する */
void print_node( NODE *p )
{
NODE *q = p;
double len = 0;
do {
printf("%d %d\n", q->data.x, q->data.y );
q = q->next;
len += distance( q->data, q->next->data );
} while( p != q );
printf("length %g\n", len );
}
/* 双方向リストの反転 */
NODE *reverse( NODE *node )
{
NODE *p = node;
do {
NODE *q = p->next; /* 次のセルを記憶しておく */
NODE *t = p->next; /* next と prev を交換 */
p->next = p->prev;
p->prev = t;
p = q; /* p を更新する */
} while( p != node );
return p;
}
/* 統合する */
NODE *merge( NODE *p, NODE *q, POINT lp )
{
double d1, d2, d3, d4;
int flag1 = 0, flag2 = 2;
/* 連結点まで移動する */
while( comp_x( p->data, lp ) ) p = p->next;
while( comp_x( q->data, lp ) ) q = q->next;
/* どちらの経路が短いか */
d1 = DIFFER( p, p->next, q->prev ); /* flag is 0 */
d2 = DIFFER( p, p->prev, q->next ); /* flag is 1 */
d3 = DIFFER( p, p->next, q->next ); /* flag is 2 */
d4 = DIFFER( p, p->prev, q->prev ); /* flag is 3 */
if( d1 < d2 ){
d1 = d2; flag1 = 1;
}
if( d3 < d4 ){
d3 = d4; flag2 = 3;
}
/* d3 d4 の場合は、q を反転すれば d1 d2 と同じ操作でよい */
if( d1 < d3 ){
flag1 = flag2; q = reverse( q );
}
if( flag1 == 0 || flag1 == 2 ){
q->prev->next = p->next;
p->next->prev = q->prev;
p->next = q->next;
q->next->prev = p;
} else {
p->prev->next = q->next;
q->next->prev = p->prev;
p->prev = q->prev;
q->prev->next = p;
}
return p;
}
/* 分割統治法による解法 */
NODE *divide_merge( int start, int end )
{
NODE *n1, *n2;
POINT p;
int d, n = end - start + 1; /* 個数 */
if( n <= MAX_SIZE ){
return make_node( start, n ); /* 自明な場合 */
}
/* 分割する */
if( divide_direction( start, n ) == TATE ){
d = divide( start, n, comp_x );
} else {
d = divide( start, n, comp_y );
}
/* 共有点の複写 */
p = point_table[end + 1] = point_table[d];
/* 再帰する */
n1 = divide_merge( d + 1, end + 1 ); /* 後ろが先 */
n2 = divide_merge( start, d );
/* 統合する */
return merge( n1, n2, p );
}
int main()
{
NODE *p;
int size = read_point_data();
p = divide_merge( 0, size - 1 );
print_node( p );
return 0;
}